K近鄰演算法（k-nearest neighbor, k-NN）在各種演算法中算是比較簡單的演算法，理解起來也比較輕鬆。

1.描述

在一個已知特徵標籤的資料集（訓練集）中，資料集的各個元素在座標空間中都是有距離的，而距離最近的資料子集一般具有相對優勢的特徵標籤數量。新資料（測試資料，沒有特徵標籤）輸入後，觀測與其相臨近的K個數據組成的資料子集的特徵標籤，其中數量最多的即是該新資料的特徵標籤。

其中，有兩個比較重要的概念：1.距離，一般採用歐氏距離度量，是歐幾里得空間裡兩點間“普通”（即直線）距離。此外還有曼哈頓距離、切比雪夫距離、閔可夫斯基距離等。2.K，是自定義引數，K選取的大小對預測準確度有很大的影響，一般在2~10之間。

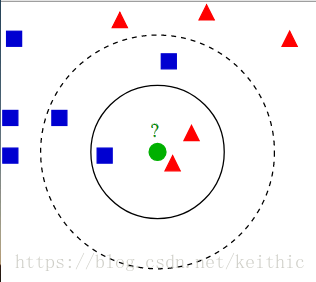
如圖所示，資料集有兩個特徵標籤（藍色方塊、紅色三角），測試樣本（綠色圓形）要麼是藍色方塊類，要麼是紅色三角類。如果 k=3（實線圓圈）它會被分配給紅色三角類，因為內圓內紅色數量居多；如果k=5（虛線圓圈）它會被分配到藍色方塊類（3個正方形與2個三角形在外側圓圈之內）。

2.演算法

輸入：訓練集    

其中，為例項的特徵向量，為例項的類別，i = 1,2,...,N；例項特徵向量x；

輸出：例項x所屬的類y。

（1）根據給定的距離度量，在訓練集T中找出與x最近鄰的k個點，涵蓋這k個點的x的鄰域記作；

（2）在中根據分類決策規則（如多數投票）決定x的類別y：

式中，I 為指示函式，即當時 I 為1，否則 I 為0。

3.程式碼實現

# -*- coding: UTF-8 -*-
import numpy as np
import operator

"""
函式說明:建立資料集

Parameters:
    無
Returns:
    group - 資料集
    labels - 分類標籤
"""
def createDataSet():
    #四組二維特徵
    group = np.array([[1,101],[5,89],[108,5],[115,8]])
    #四組特徵的標籤
    labels = ['愛情片','愛情片','動作片','動作片']
    return group, labels

"""
函式說明:kNN演算法,分類器

Parameters:
    inX - 用於分類的資料(測試集)
    dataSet - 用於訓練的資料(訓練集)
    labes - 分類標籤
    k - kNN演算法引數,選擇距離最小的k個點
Returns:
    sortedClassCount[0][0] - 分類結果
"""
def classify0(inX, dataSet, labels, k):
    #numpy函式shape[0]返回dataSet的行數
    dataSetSize = dataSet.shape[0]
    #在列向量方向上重複inX共1次(橫向)，行向量方向上重複inX共dataSetSize次(縱向)
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
    #二維特徵相減後平方
    sqDiffMat = diffMat**2
    #sum()所有元素相加，sum(0)列相加，sum(1)行相加
    sqDistances = sqDiffMat.sum(axis=1)
    #開方，計算出距離
    distances = sqDistances**0.5
    #返回distances中元素從小到大排序後的索引值
    sortedDistIndices = distances.argsort()
    #定一個記錄類別次數的字典
    classCount = {}
    for i in range(k):
        #取出前k個元素的類別
        voteIlabel = labels[sortedDistIndices[i]]
        #dict.get(key,default=None),字典的get()方法,返回指定鍵的值,如果值不在字典中返回預設值。
        #計算類別次數
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    #python3中用items()替換python2中的iteritems()
    #key=operator.itemgetter(1)根據字典的值進行排序
    #key=operator.itemgetter(0)根據字典的鍵進行排序
    #reverse降序排序字典
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #返回次數最多的類別,即所要分類的類別
    return sortedClassCount[0][0]

if __name__ == '__main__':
    #建立資料集
    group, labels = createDataSet()
    #測試集
    test = [101,20]
    #kNN分類
    test_class = classify0(test, group, labels, 3)
    #列印分類結果
    print(test_class)
 

歐氏距離概念：

在歐幾里得空間中，點x =(x1,...,xn)和 y =(y1,...,yn)之間的歐氏距離為

                  

向量的自然長度，即該點到原點的距離為

                  

它是一個純數值。在歐幾里得度量下，兩點之間線段最短。

李航《統計學習方法》