題目描述

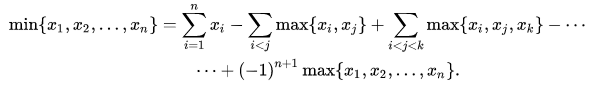
大概就是這麼兩個東西，做題思路大概就是正難則反吧，max不好求但min好求，就可以直接用這種方法上了。

現在我們算maxV(S)，然鵝它不好算，所以我們就轉換求所有minV(S)。

考慮一個事件發生的概率為p，那麼我們就有了求min的方法。

sum=1*p+2*(p-1)*p+3*(p-1)^2*p......

然後用高中數學知識，解得它等於1/p。

然後我們的任務變成了求所有子集的p。

這玩意也不太好求，因為所有與這個集合有交的數都會產生貢獻。

再次正難則反一下，變成了1-補集，這個補集和很好，它就是補集的高維字首和。

有人說這是FMT，但好像FWT的異或卷積也長這樣？

程式碼

#include<iostream>
#include<cstdio>
#include<cmath>
#define N (1<<20)+20
using namespace
 
 std;
const double eps=1e-10;
int n,size,cnt[N];
double ans,a[N];
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(f=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x; 
} 
int main(){
    n=rd();size=(1<<n);int
 
 up=size;
    for(int i=0;i<size;++i)scanf("%lf",&a[i]); 
    for(int i=1;i<size;i<<=1)
        for(int j=0;j<size;++j)if(!(j&i))a[j|i]+=a[j];
    for(int i=1;i<=size;++i)cnt[i]=cnt[i>>1]+(i&1);
    for(int i=1;i<size;++i){
        double x=1-a[(size-1)^i];
        if(fabs(x)<eps){printf("INF\n");return 0;}
        if(cnt[i]&1)ans+=(double)1/x;else ans-=(double)1/x;
    }
    printf("%.10lf",ans);
    return 0;
}

我看到網上還有這麼一種解法

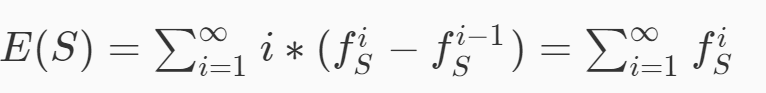
然而我並沒有看懂。。。