高等數學筆記第四天
0/0, ∞/ ∞ 未定式的處理:
洛必達法則:(適用於 0/0型 未定式)
內容: 若 lim f(x)/F(x) = 0/0, 則有 f(x) / F(x) = lim f'(x) / F'(x) ,注意,它對於: x-> A 或者 x-> ∞都適用。
前提: lim f'(x) /F'(x) = A 或者 ∞;
若lim f(x)/ F(x) = ∞/ ∞, 也可以適用洛必達法則;
趨於∞的速度,對數函式 < 冪函式 < 指數函式.
對於較為複雜的式子,應當及時分離 非零 極限的乘積 因子,可減少計算量。 此外,可使用等價無窮小的替換。(前提是必須為等價無窮小才行)。
常見的三個等價無窮小:
1.指數: ![]()
2.對數: ln(1 + x) ~ x;
3.冪數: ![]()
其它未定式的處理:
1. ∞*0 型未定式:
lim f(x)*g(x) ----簡單因子放入分母--->  , 即 轉化為: 0/0 ,或者 ∞/∞;
, 即 轉化為: 0/0 ,或者 ∞/∞;
2.∞-∞型未定式:
lim [ f(x) - g(x)] --->通分 或者 分母 有理化 ; 即 將 整式 轉換為 分式;
eg: lim sec x - tan x , x-> π/2; ![]()
3.冪指函式:
方法見之前的筆記。
eg: lim x^x,x -> 0+;  ;
; 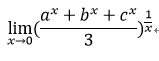
泰勒公式:
內容: 設 f(x) 再 x0 處有 n 項導數,則 存在 x0 的一個領域,對於該領域 內任一點x 有:
f (x) = f(x0) + f'(x0)(x-x0) + f''(x0) / 2! * (x-x0)^2 + ...... + f^n(x0) / n! * (x-x0)^n + Rn(x);
其中,Rn(x) 為 餘項, Rn(x) = O( (x-x0)^n), 讀作: Peano餘項。
泰勒中值定理:
內容: 若f(x) 在 x0 的領域記憶體在 直到 n+1 階 的導數,則x0 的某個領域內有:
f(x) = f(x0) + f'(x0)(x-x0) + f''(x0) / 2! * (x-x0)^2 + ...... + f^n(x0) / n!(x-x0)^n + Rn(x).
其中,Rn(x) = f^(n+1) (ξ) / (n+1)! * (x-x0)^ (n+1), ξ在 x 與 x0 之間 ;Rn(x) 稱為 拉格朗日餘項
即 ξ = θx + (1-θ)x0, θ∈(0,1);
麥克勞林公式:
內容: 泰勒公式在x = 0 時的情況:
即 f(x) = f(0) + f'(0)*x + f''(0)/2! * x^2 + ...... + f^n(0) /n! * x^n + Rn(x)
帶拉格朗日餘項的麥克勞林公式: Rn(x) = f^(n+1) (θ*x)/(n+!)! * x^(n+1), θ∈(0,1);
常見的麥克勞林公式:
1.餘弦: ![]()
2.正弦: 
3.指數: 
4.對數: ![]()
5.冪數: ![]()
駐點,可能為不可導點,也可能為極值點。
極值的第一充分條件:
1.點x0處連續;
2.點 x0 的去心 領域可導;
3.f'(x0-) 與 f'(x0+) 導向
極值的第二充分條件:
1.f'(x0) =0,且f''(x0)=/= 0;
2.若 f''(x0) <0,f(x0) 為極大值
3.若 f''(x0) >0,f(x0) 為極小值
曲線的凹凸性:
1. ,即 弦終點 > 弧中點,為上凹, 此時 f''(x) >0; 即一階導遞增,斜率值逐漸變大;
,即 弦終點 > 弧中點,為上凹, 此時 f''(x) >0; 即一階導遞增,斜率值逐漸變大;
2.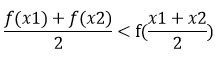 ,即 弦終點 < 弧中點,為上凸, 此時 f''(x) <0; 即一階導遞減,斜率值逐漸變小;
,即 弦終點 < 弧中點,為上凸, 此時 f''(x) <0; 即一階導遞減,斜率值逐漸變小;
曲線凹凸性的判定定理:
若f(x) 在 [a,b] 連續,在(a,b) 上二階可導,則 f''(x) <0 時,為凸; 若 f''(x) >0,為凹。
拐點: f''(x0) =0,拐點指: (x0,f(x0) )
可能出現拐點的是: f''(x) =0的點 或者 f''(x0) 不存在的點。
求駐點 或 拐點 的步驟:
1.確定定義域;
2.尋找駐點;(一階導的時候,已經包括尋找不可導點。)
3.尋找不可導點;(二階導確定不可導點,必須根據一階導確定。)
斜漸進線:(稱之為線,但是它只在某一點有意義。)
y=kx+b, 其中,![]() ,
, ![]()
不定積分:
1.定義: 連續函式一定有原函式,且原函式可導,且不唯一。
運算式: ![]()
其中,![]() 稱為積分號, f(x) 稱為 被積函式; dx 稱為: 積分變數; F(x) 稱為 原函式, C為 常數
稱為積分號, f(x) 稱為 被積函式; dx 稱為: 積分變數; F(x) 稱為 原函式, C為 常數
2.常見函式不定積分表:
1. 原一次冪函式: ∫k dx = kx +C
2. 原普通冪函式: ∫ x^u dx = x^(u+1) / (u+1) + C
3. 原對數函式: ∫ 1/x dx = ln|x| +C
4. 原三角函式相關:
原正弦: ∫ cosx dx = sinx +C
原餘弦: ∫ sinx dx = - cosx +C
原正切: ∫ 1/cos^2(x) dx= ∫sec^2(x) dx = tanx + C
原正割: ∫ sec(x)*tanx dx = sec x +C
原餘割: ∫ csc (x)*cotx dx = -csc x + C
原餘切: ∫ 1/sin^2(x) dx =∫ csc^2(x) dx = -cot x +C
原反正弦: ∫ x/ √(1-x^2) dx = arc sin x +C
原反餘弦:待定
原反正切: ∫ x/(1+ x^2) dx = arc tanx + C
原反正割: 待定
原反餘割:待定
原反餘切:待定
5. 原指數函式:
普通指數: ∫ a^x dx = a^x / ln(a) + C
特殊指數: ∫ e^x dx = e^x +C
常見的積分聯想:
1. 1/(x^2 +1) ~ arc tan x
2. tan^2(x) ~ sec^2(x)
3. sin^2(x/2) ~ 二倍角公式;
二倍角公式:
1. sin^2(x) = (1- cos 2x) /2;
2. cos^2(x) = (cos 2x +1) /2;
3. cos 2x = 2*(cosx)^2 -1 = 1- 2*(sinx)^2;
換元積分法:
第一類換元法:
若 ∫ f(u) du = F(u) + C, F'(u) = f(u), 則 ∫ f( g(x) ) * g'(x) dx = [ ∫ f(u) du ], u = g(x);
關鍵: 1.外函式可積; 2.內函式湊微分;
eg: 

![]()

常見微分收納等式:
1. 冪函式相關: ∫ f(x^n)*x ^(n-1) dx = 1/n ∫ f(x^n) d x^n
2x dx = d x^2
1/x^2 dx = - d 1/x
1/√x dx = 2d√x
1/x dx = d lnx
2.三角函式相關:
sinx dx = - dcos x
cos x dx = dsinx
割與切的關係:
(tanx)^2 +1 = (secx)^2;
(cotx)^2 +1 = (cscx)^2;
∫csc x dx = ln | csc x - cot x | +C
∫ sec x dx = ln | sec x + tan x| + C
∫ tanx dx = - ln|cos x| + C
∫ cot x dx = ln |sin x| + C
三角函式積化和差公式:
sinxcosy =1/2 *[s(x+y) + s(x-y)]
cosxcosy =1/2 *[c(x+y) + c(x-y)]
sinxsiny = -1/2 *[c(x+y) - c(x-y)]
3.指數: e^x dx = d e^x;
第二類換元法(反解x):
步驟: 1.換元: x= g(t) ;
2. dx = g'(t)dt
3.求出 F(t) + C ,回代: t = g^(-1) (x), 反函式。
常見代換:
1.有理代換:(一次式,一次式相除)
∫ (![]() )dx ,令 u =
)dx ,令 u = ![]() 求解;
求解;
2.三角代換(二次式):
![]() , 可令: x = asin t
, 可令: x = asin t
![]() , 可令: x = a sec t
, 可令: x = a sec t
![]() , 可令: x = a tan t , 或者 a cot t ;
, 可令: x = a tan t , 或者 a cot t ;
注意: 三角代換的回代 , 需要使用 勾股定理;
3.倒數代換:(分母較高時適用)
即 令 x = 1/t, 求解。
分佈積分法:
1.形式一: ∫ u v' dx = uv - ∫u' vdx, 步驟: 觀察 --》 湊微分---》 分步積分
原則: 1.dv要容易湊出; 2. ∫vdu 比 ∫u dv 容易;
2. 形式二:∫ udv = uv - ∫vdu
總結(注意,這裡的uv是形參,雖沒有實際意義,但是一旦確定,它便具有了位置屬性。從形參而言,預設v的複雜度是要高於u的。 原函式中,v'是將複雜度高的函式進行展開,加大整體複雜度; ∫vdu則是期望uv二者均往小的複雜度上運算):
uv的選取:
冪函式 與 指數函式,對數函式相乘時,冪函式 作為 u;
相對的,當冪函式與 對數,反三角函式相乘時,選冪函式 作為 v;
基本函式中,選取u的優先順序: 反,對,冪,指,三;
注: 微分收納的前提: 內部一致,eg: cos 3x dx =/= d sin3x = 1/3 dsin3x
有理函式的積分:(拆分式)
有理函式的分類:
1.真分式: 分子最高次< 分母最高次
2.假分式: 分子最高次> 分母最高次
真分式:
對真分式p(x)/q(x),若分母可分成 兩個 多項式 乘積, 即 q(x) = q1(x1)*q2(x2),且它們無公因式,則它們一定可以拆分成兩個真分式之和。 即:
二次多項式不能拆分,則能拆分成 a^2 + b^2的方式;
