定積分:

           定義：是函式f(x)在區間[a,b]上的積分和的極限；（定積分，與 不定積分 僅僅在數學上有一個計算關係（牛頓-萊布尼茨公式），其它一點關係都沒有！）。

                    （a,b）上的定積分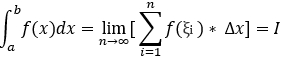：  ， ，其中，a稱為積分下限，b稱為 積分上限；ξi 稱為尼曼積；

             它有這樣的一些屬性：

                    1.任意劃分區間；  2. 任意取點；   3.求和； 4.取極限；

                    其中的劃分的區間長度：定義為： λ，  則 有： λ=1/n;  

                     注意： λ-> 0  ===>  n->∞,  n->∞  ===/=>  λ-> 0;  因為n代表份數，當分的份數無窮多的時候，並不能保證分到區間無窮小。

          物理意義：

               1.曲邊梯形的面積；   2. 變速直線運動的路程；

           幾何意義：

                 若 f(x) >0， 則為曲邊梯形的面積；

                 若f(x) <0,    則為曲邊梯形面積的負數；

                 若f(x) 有正有負，則為： A1-A2+A3

          可積性：

                  1.在閉區間上連續的函式是可積的；

                  2.在閉區間上有界，且只有 有限個 間斷點的函式 是 可積的；

          不可積性：

                   1.迪利克雷函式：  d(x)    = 1, x是有理數；  =0，x 是無理數；

                前n個數的平方和公式： 

定積分與不定積分的唯一聯絡：

        eg: 

       自我理解（僅供自己理解用，有可能是錯誤的）：就冪函式而言， 一個函式具有無數個相差為常數的 不定積分函式，這些函式一定會有一些與x軸相交。任選一個不定積分函式，任取一點 x0,它的函式值 的絕對值 代表了長度資訊；長度的起始點必定為零點。   因此，不定積分的函式值 = 該方向上（正負代表方向） 最近的零點  到該點的 原函式的 定積分值。  也即： 該方向上（正負代表方向） 最近的零點  到該點的 原函式與 x的面積。

         即： 若： F'(x) = f(x),且 當F(x) =0時，x= x1,x2,x3....  則  F(a) = 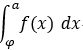  ，其中，φ為同方向上的前一個零點；

          另外注意，不定積分函式中，常數項均可以視為0，則冪函式而言，若有定義，總存在F(0) =0;  對於其它基本初等函式，若不存在零點的，就以-無窮或正無窮代替。

定積分性質：

       規定：   

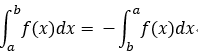
       1.若f(x) ,g(x) 在[a,b]可積，則  

       2.若 f(x) 在 [a,b] 可積，則：

       3.若 a<c<b， 則： 

       4.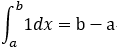   以及：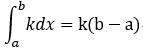

       5.若[a,b]上恆有： f(x) >= 0, 則 

               推論1： 若[a,b]上，f(x) <= g(x) ,則  

               推論2:   |   | <= 

       6.若f(x) ∈ [m,M] ，則 有 m(b-a) <= <= M(b-a)

       7.若f(x) 在 [a,b]上連續，則 [a,b] 上 至少存在一點： ξ, 使得：  = f( ξ)(b-a), 對 ξ在(a,b)也同樣成立；  積分中值定理。   f( ξ) =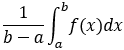，稱為函式f(x) 的平均值；

   微積分的基本公式:

          1.函式的變上限函式(積分上限函式)及其導數：

                   1.定理一： 若f(x) 在[a,b] 連續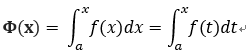，,則  Φ'(x) = f(x);  t代表與x無關的表示式；

                   2.定理二： 若f(x) 在 [a,b]上連續，則 ： 

          2.牛頓-萊布尼茨公式：

                若F(x) 是連續函式 f(x) 在 [a,b]上的一個原函式，則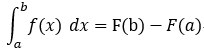 

                作用： 利用不定積分求定積分；

                推論： 

                       1.變下限函式：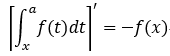 

                          推論：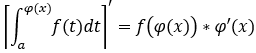 

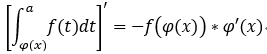
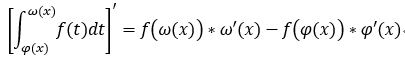
定積分換元法：

        假定 f(x) 在[a,b]上連續，x = φ(t),滿足： 1.φ(α) = a,φ(β) =b   2.φ(t) 在[α,β]上連續可導，且值域為：R =[a,b]

            則有：  

            注意： 

                  1.換元 同時 換限

                  2.只需將新變數t的上下限帶入即可，而不用像不定積分那樣反解出x；

                  3.不要求 x= φ(t)是單調的，因為不用回代。

       對稱區間定理：

                 奇函式在對稱區間的定積分為零；

                 偶函式：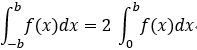 

                 eg:  

       常見函式的換元技巧：

              1.三角函式：

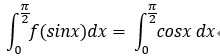
             2.周期函式：

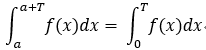                       ，即周期函式 的 定積分值，只與區間長度有關，與起始點無關；

定積分的分步積分公式：

           或者

無窮積分：

        它的步驟： 1.計算定積分；  2.求極限；

定積分在幾何上的應用：

     見高等數學下冊！