常數項級數：

      概念： 用圓內接正多邊形面積逼近圓面積，依次作圓內接正 3*2^n (n=0,1,2 ... L)邊形，設  a0 表內接正三角形面積，ak 表增加的面積， A = a0+ a1+L + an+ L;

       定義： 給定一個數列，u1,u2,L , un, 其為  常數項無窮級數(一般項，或者通項): u1 + u2 + L + un + L 的部分

       部分和： 

                   

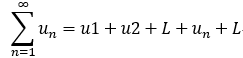
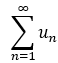                   稱為的部分和；

        斂散性： 

                      若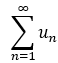的部分和數列 {sn} 有極限s,  則 稱 無窮級數收斂；

等比級數（幾何級數）：

         斂散性:   |q| <1 時，等比極數收斂；

                        |q| >=1 時， 等比級數發散；   其中，q指的是 等比公項；

         性質1:  若等比級數收斂，則其k倍仍然收斂；

         性質2：若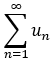 與 均收斂，則 也收斂，且 和為： s1+s2;

                  另： 收斂級數 + 發散級數 = 發散級數；  發散級數+ 發散級數 不一定= 發散級數；

                         如： Un = (-1)^(2n)   Vn = (-1)^(2n+1);

          性質3： 在級數中去掉 有限項，不影響斂散性；

          性質4： 若加括號後的級數發散，則原級數必發散；（發散級數 去 括號後  所形成的 級數 必發散）

                        注意： 收斂級數 去 括號後 所形成的 級數不一定收斂；

                        若級數收斂，則對級數的項任意加括號後仍收斂；

收斂級數的必要條件：

          1.若級數 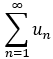 收斂，則 必有： 

                 其逆否命題：   ==> 級數發散；  （判斷級數發散的方法）

             eg: 證明調和級數: 是發散的。（反證法）

                 若收斂，有 ,    ,矛盾。

          2. 若級數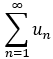收斂，則 發散；

常數項級數審斂法：

        定義法： 部分和極限存在；

        1.正項級數 Un >=0   <==> 部分和數列Sn 有界；（不常用）

         2.比較審斂法： 

                 設 ,  是兩個正項級數，對 ∀n ∈ N, 有： Un (弱) <= Vn (強), 

                 則： 1.若級數 收斂，則也收斂；

                          2.若級數發散，則也發散；

        3.P級數：

                 

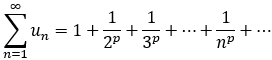
               當  0<p<= 1時，p級數發散；

               當  p>1時， p級數收斂；

         4.比較審斂法的極限形式：

                

             當 0<L <∞ 時，兩個級數 同時收斂 或者 同時發散；

             當 L =0 且 收斂時， 也收斂；

             當 L =  ∞ 時，且發散時，也發散；

          eg: 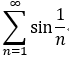發散；    注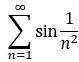： 收斂

正項級數審斂法的乘法形式：

       取   則： 

          ，其中L  為 非零常數。

                 此時，若 0<p<=1, 則 發散。   (極限審斂法)；

                            若 p>1  或者 p = ∞時， 級數收斂。

比值審斂法（達朗貝爾判別法）：

        若 為正項級數，且 

          則： 若 0<= ρ<1時，級數收斂；

                  若 ρ>1  或者  ρ=∞時，級數發散；

                  注意，這裡剛好與p級數的情況相反；

                 若 ρ=1時，不能適用；

交錯級數審斂法（符號一正一負交替出現）：

        1.萊布尼茲定理： 

               若交錯級數滿足條件：

                   1.若  U n >= U n+1 ,(數值分佈而言)；

                   2.

               則級數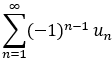：收斂，且 其和 S <= u1 ,  餘項和 Rn <= U n+1

               若交錯級數收斂，其絕對值後仍然收斂，稱為 絕對收斂， 如：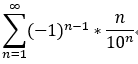 

               若交錯級數收斂，其絕對值後發散，稱為 條件收斂，如：， 

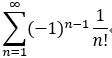
      2.絕對收斂的級數一定收斂.(判斷交錯級數的斂散性  或者 一般級數)；

              eg:

冪級數：

    函式項級數的概念： 

          為定義在 區間 I 上的函式項級數；

            對 x0 ∈ I, 若它 收斂，則稱 ： x0 為 收斂點，所有的收斂點全體稱為 收斂域；

                              若它 發散，則稱： x0為發散點， 所有的發散點全體稱為發散域；

              eg: 

                      當： |x| <1時，收斂， 此時 S(x) = ,稱為 和函式；

                              |x| >1時，發散.

           冪級數的標準形式：

                   ，取 x0 = 0, 則有：

                             

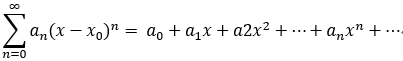
            冪級數收斂域特點：

                   關於原點對稱；

             阿貝爾定理： 

                    若冪級數在 x= x0 (x0=/=0) 處收斂，則此冪級數在滿足不等式  |x|<= |x0|的一切x處絕對收斂。 (x0 稱為收斂半徑，記作R)

                     反之，若冪級數在x = x0 處發散，則對於 |x| > |x0| 處的x發散；

                     當R = 0時，冪級數僅在x = 0 處收斂；

                     當R = +∞時，冪級數在 （-∞，+∞）收斂；

                     當R =/=0 和 +∞ 時，

                                     當|x| < R 時，冪級數絕對收斂；

                                     當|x| > R 時， 冪級數發散；

                                     當|x| = R 時，可能收斂，也可能發散，需要單獨討論；

                       若冪級數 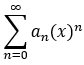 的係數滿足： 

                            則 當   ρ=/= 0 時， R = 1/ ρ;

                                 當   ρ=0  時， R  = +∞；

                                 當  ρ= +∞時，R = 0； 

                             即： 收斂半徑 R = 

冪級數的運算：

       運算後的收斂域 =  min{r1,r2};

        

        

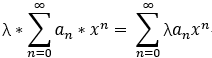
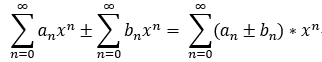
       連續性： 和函式在 收斂域內 連續；

       可積性： 和函式在收斂區間可積分，並且可逐項積分；

             即：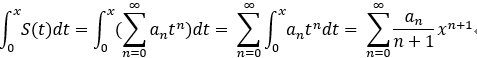 

        可導性： 和杉樹在收斂區間可導 ，且可  逐步求導；

             即：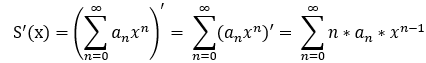 

         eg:  求冪級數 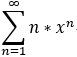  的和函式  S(x);

               注意: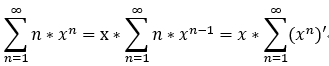  

               另：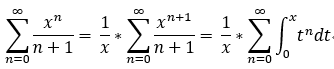 

泰勒級數：

       

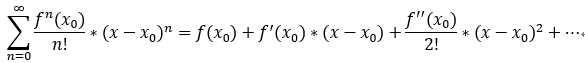
        當 x0 =0 時，稱為：  麥克勞林級數；

        展開成泰勒級數的充要條件：  通項的極限 為 0； 

         展開的方法包括： 

              1.直接展開法，利用泰勒公式；

              2.間接展開法, 利用已知函式 形式轉化；

        eg: 將 1/(1+x^2)  展開成冪級數：

                 提示:    -->   -->   --> 

        eg: 將 f(x)  = ln(1+x) 展開成 冪級數： 

                 解析：    

          理解：它們的關鍵在於： 處理好 形參，與實參，以及處理過程，複合函式，的區別與聯絡；

    

傅立葉級數：

      S(n) =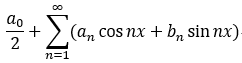   

     定理一： 

                組成三角級數的 函式系： cosx , sinx , cos2x,sin2x,... ,cosnx sinnx,L 在 [-π，π] 上 積分等於0 

                則 相同的函式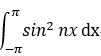 =2π ， =π  ; 

      定理二： 

                 設 f(x) 是 週期為 2π  的周期函式，且 f(x) = ,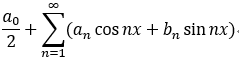

                 則有 傅立葉係數： 

                      

                     

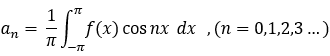
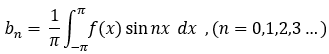
                將傅立葉係數 代入 形式傅立葉級數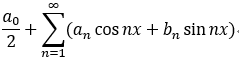： ， 則為傅立葉級數；

        定理三(迪利克雷充分條件):

               設 f(x) 是週期為 2π 的周期函式，若滿足： 

                   1.在一個週期內連續，或只有有限個第一類間斷點

                   2.在一個週期內至多有有限個極值點

                   則 f(x) 的傅立葉級數收斂，其收斂點為：

                       

        定理四：

               正弦級數 與 餘弦級數：

                 若f(x) 為 奇函式， 則 f(x)cosnx 是 奇函式， f(x)sin nx  是 偶函式；

                       故有： 正弦級數：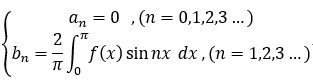  

                若 f(x)為 偶函式， 則 f(x)cos nx 為偶， f(x)sin nx 為 奇，

                       故有：餘弦級數：