二元函式：

       定義：∀(x,y)∈ D ⊆R^2, 存在唯一的 z∈R,使得  (x,y) --f->z

                記作： z = f(x,y),(x,y)   ∈D.

                注意：定義域必須記為集合形式，{(x,y)|  x與y滿足的條件};

       二重極限

           嚴格定義：  ∀ε>0, ∃δ>0,當 0<√(x-x0)^2 + (y-y0)^2 < δ時，有，|f(x,y) - A| <ε;

                     稱為：二重極限

                     記作：

           eg: 求極限：   ;   

                 求極限：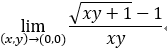 

      二元函式的連續性：

            或者： 

            一般情況下，二元函式適用 

連續是一種特殊的極限。

偏導數： 

         二重函式： f'(x0,y0) = 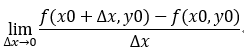表示對x的偏導數；

        導數的本質： 增量比極限；

注意： 二重函式可導 不一定連續；

偏導數的記法：

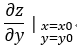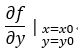       ，     ，或者

偏導函式：  關於各自變數的偏導

二階偏導：

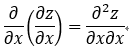          ，f''xy 與 f''yx  類似

二階混合偏導數性質：

     二階混合偏導數f''xy 與 f''yx 在區域D內連續，則該二階混合偏導數必相等。

拉普拉斯方程：

      對等二重函式的二階偏導和為零，即：

求一點處的偏導數的方法：1.先帶後求； 2. 先求（函式）後代；3.利用定義（分段點）；

全微分：

     dz =  + ;

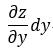     定義：

           ∆z = f(x0+∆x,y0+∆y) - f(x0,y0)

          若∆z = A*∆x + B*∆y+O(√(∆x)^2+(∆y)^2 )成立，則可微

          取： dz = A∆x + B∆y

          即：dz =  + ;

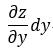  可微，可導，連續之間的關係（這裡不涉及極限）：

     一元:  可微 --> 可導  ；    可導 --> 可微        可導-->連續；  連續- /->可導；

     二元：可微 --->可導；     可導--/->可微；    可微-->連續；  偏導連續+可導---> 可微

              連續不一定可導，可導不一定連續；

 證二元函式不可微的關鍵：  O(√(∆x)^2)+(∆y)^2)不是 ∆z的高階無窮小；

          eg: 

複合二元函式的全導數：

     1.二元和一元複合：即：z=f(u,v),u=f(x),v = f(x)

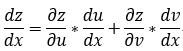
     2.二元和二元複合：即：z=f(u,v),u=f(x,y),v=f(x,y)

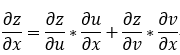
     3.二元同時與一元與二元混合： 即： z= f(u,v),v=f(x,y); u = f(x)

    4.自變數與複合函式同級的情況： 即：z=f(v,x,y) , v=f(x,y)

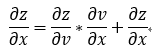
複合多元函式的高階（二階）求導：

     關鍵：一階偏導仍然是一個複合函式。

     eg: w=f(x+y+z,xyz),求 ∂w/∂x,    ∂^2 w  / ∂x∂z