微分方程：

   定義： 含有未知函式，未知函式的n階導數，以及自變數關係的方程。（其中，未知函式的n階方程必須有）；

   分類:    常微分方程；  偏微分方程；

   常用概念： 

         最高階導數的階數 稱為 微分方程的階；

         微分方程的解：使微分方程成為恆等式的函式y；

                通解

                特解：  不含任意常數的解，其圖形為積分曲線；

         初始條件(或初值條件)： 確定 通解中 任意常數的條件；

                     通解不一定是全部解，如： (x+y)y' = 0;

                 驗證通解的步驟： 1. 證明解；   2.證明通解；

可分離變數的微分方程：

           考慮如下一階微分方程，

            其難點： 不能通過等式兩邊 積分求解；

            處理： 變換。   

                        --> 方程左邊只含有 y的表示式；

                        --> 方程右邊只含有  x的表示式；

             定義： 若一個微分方程可寫成   g(y)dy = f(x)dx，則稱其為可分離變數微分方程。（一般情況下為一階）；

齊次方程：

          定義：方程項數的次數整齊，並且次數 >= 2，若為n,同除 一個 x^n,能夠得到形如：y'= 的方程；

          公式：   ,其中，固定不變；

一階線性微分方程：

          定義： 微分方程形如： y' + P(x)*y = Q(x),其中x 近似看成常數，y與y' 看成變數；

          分類：

                齊次式（Q(X)=0的情況）：分離變數法 --->  (通解)  

                非齊次式（Q(x)=/=0）：齊次的通解 +  一個非齊次的特解；

                    常數變易法(方法一)：  

                       假定  ,--> -->  -->

                    公式法（方法二）：

                  關鍵點： 在基本初等函式中，只有e^x 的導數是他本身，以上的兩種方法都是基於這個思想；

        練習題：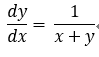 

               法一： 

               法二： 令x+y = u, y = u-x, 

普通高階線性微分方程：

       伯努利方程：  

        解法：經過變數代換，化為 一階線性微分方程，變數代換需要依據具體情況而定。

可降階的高階微分方程：

         y'' = f(x,y,y');

        1. y^m = f(x): 一次積分；

         2.y^m = f(x,y'): 依次求 y^(m-1), 再向上回溯。（令 y' = P(x) ）

         3. y^m = f(y,y'): 令 y' = P(y), 則  y'' = P* (dp/dy);

二階線性微分方程：

        形如:  y'' + P(x)y' + Q(x)y = f(x)

       齊次解的結構( f(x)=0的情況 )：

             設C1y1+ C2y2（一般模型）, 若y1,y2線性無關，即是通解（亦可稱為 線性無關特解）。

                 兩個函式線性無關的充要條件：

                  做題時，應先判斷解的線性無關性；

         非齊次解的結構( f(x)=/=0 的情況)：

               y=     Y(x) + y^* (x)

               設： (k=1,2 ... m) 分別時方程： 的特解，

                則解的疊加性： 

        eg: y'' + P(x)y' + Q(x)y = f(x)有三個解： y1 = x,y2=e^x, y3 = e^3x,求此方程滿足初始條件： y(0) =1,y'(0)=3的特解。

               提示:  y2-y1 與  y3-y2時對應齊次方程的解。

常係數二階齊次線性微分方程：

        y'' + py' + qy =0 ==> r^2 + rp +q = 0;

      待定係數法： 各階導數可合併，則假設： y = e^(rx)

            1.當 ∆> 0 時，其解： (注：微分方程一般都是 求通解)；

            2.當 ∆= 0 時，可對應一個特解.  y1 = e^(rx),  令 y2 = u(x)*e^(rx),然後求 u，可取特解u=x,則 y2 = x*e^(rx).

                     其通解為： y= c1*e^(rx) + c2*x*e^(rx) = e^(rx)* (c1+c2*x);

            3.當 ∆< 0 時，r = ，（共軛復根）

                     尤拉公式： ，被稱為： 數學中的天橋，由泰勒公式推到而來；

                      它經過若干次化簡後，可以得到通解：  

                   eg:   y'''' - 2y''' + 5y''=0  ==> r^4 - 2*r^3 +5*r^2 =0;  --> r1=r2=0;  r3,r4 = 1+- 2i, （虛數）;

                          y= (c1+ c2*x)*e^(0x) + e^x * (c3 cos2x + c4 sin2x);

常係數非齊次線性微分方程：

            y'' +p*y' +q = f(x);

          f(x)的情況有：

            1.，（m表次數），求 y* = e^(λx),Q(x), 即求 Q(x);

                   代入得: Q''(x) + (2λ+p)Q'(x) +(λ^2 + pλ+q)Q(x) = 

               若等式左右的次數相等： 

                       1.當 λ^2 + pλ+q =/=0時， 即 λ不是特徵根，記為： 

                       2.當 λ^2 + pλ+q =0 且 2λ-p =/=0時，即  λ 是單根，記為： 

                       3.當 λ^2 + pλ+q =0 且 2λ-p=0時，即 λ 是重根，記為： 

                記為：,其中，k 表根的情況，如0重根 (λ通常是已知的)，1單根，雙重根。

        eg:  求 y'' -2y' -3y = 3x+1的一個特解，有λ=0,m=1

                  思路： 有： y* = ,可令： ，代入原式；

        eg: 求 y'' -5y' +6y = x*e^(2x)  的通解；