迴歸問題是通過一系列的已知資料預測未來的值，這個待預測的值是一個連續值。我們使用20世紀70年代中期波士頓郊區房價的資料來進行迴歸問題的討論。

資料準備

同樣的，我們可以使用Keras的內嵌函式載入這批資料，如果網路不支援自動下載，你可以選擇事先下載好的資料。

from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) = 
boston_housing.load_data(path='/ABS_PATH/boston_housing.npz')
print(train_data.shape, test_data.shape)
print(train_data[0], train_targets[0])
 

(404, 13) (102, 13)

[ 1.23247 0. 8.14 0. 0.538 6.142 91.7 3.9769 4. 307. 21. 396.9 18.72 ] 15.2

可以看出這組資料有404個訓練樣本和102個測試樣本，每個樣本都有13個數值特徵，預測的目標是波士頓郊區房屋價格的中位數（單位是千美金）。這些數值特徵由於各自的單位不同，取值範圍與大小參差不齊，如果直接將這組資料輸入到神經網路，勢必增加模型學習的困難。所以，我們需要對每個特徵進行標準化操作，即對輸入資料的每個特徵，減去特徵的平均值，再除以標準差。

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std
print(train_data[0])
 

[-0.27224633 -0.48361547 -0.43576161 -0.25683275 -0.1652266 -0.1764426 0.81306188 0.1166983 -0.62624905 -0.59517003 1.14850044 0.44807713 0.8252202 ]

構建網路

我們已經有了電影評論極性分析的實踐經驗，可以很輕鬆地堆疊出一個網路模型出來，在這裡我們把網路的構建功能封裝成了一個函式，為了後面多次使用它。

from keras import models
from keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu', input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model
 

這個網路模型包含兩個中間層，每層都是64個隱藏單元的全連線層，對於第一層需要指定輸入資料的維度，我們選擇ReLU作為啟用函式（你會發現這種帶有ReLU啟用的Dense層的堆疊，是非常有用的結構，可以解決很多種問題）。這裡值得我們注意的是網路的最後一層只有一個單元，沒有啟用，它是一個線性層，這種設定是標量回歸的典型配置。對於迴歸問題，損失函式通常選擇均方誤差（MES, mean squared error）;訓練過程需要監控平均絕對誤差（MAE, mean absolute error）。

驗證方法

在分析資料時我們已經看到，這批資料的樣本量是很少的（只有幾百個），如果我們仍然把訓練集拆分為訓練和驗證集，勢必導致訓練資料不足，同時驗證資料太少引發驗證得分的波動。所以，在資料樣本量較少的情況下，我們建議使用K折交叉驗證，這種方法首先將資料集劃分為K個分割槽，例項化K個相同的模型，將每個模型在K-1個分割槽上訓練，並在剩下的一個分割槽上進行評估，把K次評估得分的平均值作為模型的驗證分數。

import numpy as np

k = 4
num_val_samples = len(train_data) // k
num_epochs = 500
all_mae_history = []

for i in range(k):
    print('processing fold #', i)
    #其中一份作為驗證資料
    val_data = train_data[i*num_val_samples: (i+1)*num_val_samples]
    val_targets = train_targets[i*num_val_samples: (i+1)*num_val_samples]
    
    #剩餘各份作為訓練資料
    partial_train_data = np.concatenate([train_data[:i*num_val_samples], 
                                        train_data[(i+1)*num_val_samples:]], axis=0)
    partial_train_targets = np.concatenate([train_targets[:i*num_val_samples], 
                                           train_targets[(i+1)*num_val_samples:]], axis=0)
    
    model = build_model()
    history = model.fit(partial_train_data, partial_train_targets, 
                        validation_data=(val_data, val_targets),
                        epochs=num_epochs, batch_size=1, verbose=0)
    
    #從hisotry中提取驗證結果
    mae_history = history.history['val_mean_absolute_error']
    all_mae_history.append(mae_history)

當然，除了從history中提取驗證結果，也可以手動獲取驗證得分，此時則不需要在fit函式裡指定驗證集。

#在驗證資料上評估模型
model.fit(partial_train_data, partial_train_targets, 
          epochs=num_epochs, batch_size=1, verbose=0)
val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0) 

我們計算出每個輪次中所有折MAE的平均值，並使用Matplotlib繪製出指標的變化曲線。

average_mae_history = [np.mean([x[i] for x in all_mae_history]) for i in range(num_epochs)]

import matplotlib.pyplot as plt

plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()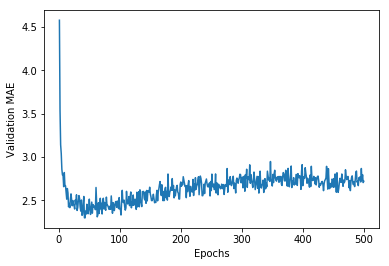

很遺憾，由於資料的方差都相對較大，圖片並沒有直觀地反映出指標的變化趨勢。我們需要採取一點小技巧重新繪製：

• 刪除前10個數據點，因為它們的取值範圍與曲線上的其他點不同
• 將每個資料點替換為前面資料點的指數移動平均值，以得到光滑的曲線

def smooth_curve(points, factor=0.9):
    smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous*factor+point*(1-factor))
        else:
            smoothed_points.append(point)
    return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:]) #剔除前10個點
plt.plot(range(1, len(smooth_mae_history)+1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()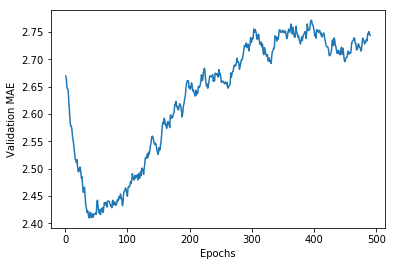

此時的曲線可以很直觀地看出，驗證MAE在60輪左右就不再顯著降低了，此後甚至出現了過擬合。我們用最好的引數（這裡只演示了調整輪數）訓練最終的生產模型，並觀察它在測試集上的效能。

model = build_model()
model.fit(train_data, train_targets, epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
print(test_mae_score)

2.7114876391840914

看來，我們預測的房價還是和實際價格相差了約2700美元。

總結

即便本節我們討論的是迴歸問題，但是與前一節的電影評論極性分類問題的建模方法論是一樣的，針對迴歸問題，我們可以總結如下：

• 迴歸問題使用的損失函式通常是均方誤差（MSE），評價指標為平均絕對誤差（MAE）
• 如果輸入的資料的特徵具有不同的取值範圍，應該先進性預處理，對每個特徵單獨進行縮放（通常減均值除方差是一種不錯的縮放手段）
• 如果資料的驗證表現受資料的分佈影響，沒有明顯的趨勢可見，可以採取一定的平滑處理以便直觀地分析趨勢
• 如果可用資料較少，K折交叉驗證是首選的驗證方法（同樣適用於分類問題）