Burnside引理和polay計數學習筆記
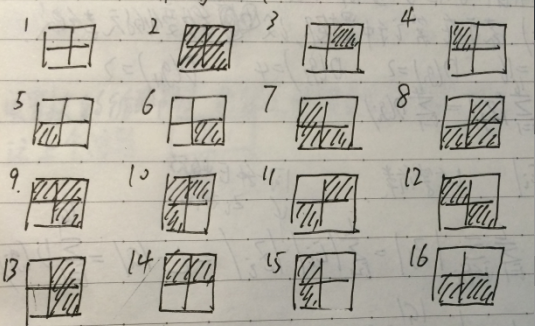
首先提出一個問題,在一個2*2的矩陣裡染色,旋轉後相同算作一種,問有多少種染色方法。
顯然窮舉有那麼多種,然後發現,(3,4,5,6)是同一種,(7,8,9,10)是一種,(11,12)是一種,(13,14,15,16),1是一種,2是一種。
發現,顏色少的時候,格子少的時候還是很容易列舉的,但是當問題規模大的時候,計算起來就會比較麻煩。
所以我們要來介紹一下Burnside定理和polay計數。
首先是Burnside定理,介紹之前,首先介紹幾個概念。
一。置換群G ,即所有的置換。以上面的為例子,置換一共有4種—旋轉0度,旋轉90度,旋轉180度,旋轉270度。所以|
二。第二個概念,Zk 對於每個元素K,這裡的K滿足1<=k<=16 ,G 中使得K保持不變的置換全體。
eg.Z1={g1,g2,g3,g4}
Z11={g1,g3}
三。第三個概念,Ek 對於每個元素k,在四種置換下依次得到G下的轉換的編號。
eg.E1={1} ,E2={3,4,5,6}
沒一個Ei 其實就是一個等價類。
根絕上述定義,很容易得到一個公式:|Ek|∗|Zk|=|G|
PS:|Ek| 是第k個元素,在四種變換下能形成的種數。
|Zk| k在|G|種置換下保持不變的個數。
G 表示置換種數
四。接著我們引出第四個概念。D 表示在第i種置換下,沒發生變換的元素個數
D(g1)=16,D(g2)=2,D(g3)=4,D(g4)=2
舉例說就是在第一種置換下,16個元素都不會發生變化,在第二種置換下,1和2元素不會發生變化。
顯然有個公式∑16j=1|Zj|=∑4i=1D(gi)
那麼我們下面來進行最後的公式推導。
n=∑Li=1|Ei| ps.L個等價類
∑nj=1|Zj|=∑Li=1∑j∈E|Zj|=∑Li=1|Ei|∗|Zi|=L∗|G|
又因為∑16j=1|Zj|=∑4i=1D(gi)
所以推出了我們著名的Burnside定理:
L=1|G|∗∑i
這就是著名的Burnside定理。 第一步求出所有的置換。第二步求出所有置換下,不變元素個數。所最開始的例子。ans=(16+2+4+2)/4=6.但是我們發現這個的第二部比較難求。所以我們接下來介紹polay計數法。
polay定理
首先先介紹一個概念—迴圈節。
觀看下一組置換(1,2,3,4,5)−>(3,5,1,4,2)
他的迴圈節是(13)(25)(4) ,所以迴圈節長度是3,兩個迴圈節是不想交的。
記上個問題按逆時針將四個格子放上1,2,3,4。
然後
相關推薦
Burnside引理和polay計數學習筆記
首先提出一個問題,在一個2*2的矩陣裡染色,旋轉後相同算作一種,問有多少種染色方法。
顯然窮舉有那麼多種,然後發現,(3,4,5,6)是同一種,(7,8,9,10)是一種,(11,12)是一種,(13,14,15,16),1是一種,2是一種。
發
Burnside引理和Polya定理
開始 多少 tails 沒有 -s 圖片 detail 最簡 方案 轉載自:https://blog.csdn.net/whereisherofrom/article/details/79631703
Burnside引理
筆者第一次看到Burnside引理那個公式的時
【數學專題】(二) Burnside引理和Polya定理
Burnside引理
筆者第一次看到Burnside引理那個公式的時候一頭霧水,找了本組合數學的書一看,全是概念。後來慢慢從Polya定理開始,做了一些題總算理解了。本文將從最簡單的例子出發,解釋Burnside引理和Polya定理。然後提供一些自己做過的和上述定理相關的
Burnside引理和Polya定理之間的聯絡
最近,研究了兩天的Burnside定理和Polya之間的聯絡,百思不得其解,然後直到遇到下面的問題:
對顏色限制的染色
例:對正五邊形的三個頂點著紅色,對其餘的兩個頂點著藍色,問有多少種非等價的著色?
其中置換的方法有旋轉 \(0^{\circ}, 72^{\circ}, 144^{\circ}, 21
等價類計數(Polya定理/Burnside引理)學習筆記
參考:劉汝佳《演算法競賽入門經典訓練指南》
感覺是非常遠古的東西了,幾乎從來沒有看到過需要用這個的題,還是學一發以防翻車。
置換:排列的一一對映。置換乘法相當於函式複合。滿足結合律,不滿足交換律。
置換的迴圈分解:即將置換看成一張有向圖,分解成若干迴圈。迴圈的數量稱為迴圈節。
以置
[學習筆記]置換群 置換群和Burnside引理,Polya定理
這是群論。
置換群是群論的一種:必須要知道的:
置換群和Burnside引理,Polya定理
理解一下;
這裡置換就是旋轉同構的表示,方案就是“染色方案”
m種置換,假如所有可能的方案,每種同構的方案都算了m次。(每種置換都有一次),那麼直接除以m即可。
但是有的方案並沒有被計
Burnside引理,Polya定理和一些計數問題(1)
變換 相同 不同的 觀察 本質 exist 關系 不變 陪集 Burnside引理
考慮一個$S$上的置換群$G$. 對於$u,v \in S$,定義它們“等價”當且僅當存在一個$G$中的置換,將$u$變為$v$.容易發現,這一關系是一個等價關系.設$E(k)$表示$k$所
置換群和Burnside引理,Polya定理
因子 不同的 mir details 構造 itl 置換群 模型 遇到 定義簡化版:
置換,就是一個1~n的排列,是一個1~n排列對1~n的映射
置換群,所有的置換的集合。
經常會遇到求本質不同的構造,如旋轉不同構,翻轉交換不同構等。
不動點:一個置換中,置換後和置換前沒有
burnside引理+polya計數法小結
WC上wwwwodddd講的整數和多項式相關裡面最後又burnside引理的一部分
被生成函式調戲瘋了的我突然斷線重連
坐在禮堂最後一排的沙發位上和老黃人瘋狂口糊
不過聽課的時候想的不是很細,重新整理了一發
大概就是
本質不同的方案數=1置換個
等價類計數:Burnside引理 & Polya定理
提示: 本文並非嚴謹的數學分析,有很多地方是自己瞎口胡的,僅供參考。有錯誤請不吝指出 :p
## 1. 群
### 1.1 群的概念
群 $(S,\circ)$ 是一個元素集合 $S$ 和一種二元運算 $ \circ $ 的合稱,其滿足以下性質。
##### 封閉性
>對於 $\forall a,b
網頁排版中的浮動和定位(學習筆記)
mage hidden alt images blog clear ul li -a www CSS中的浮動和定位
在了解CSS中的浮動和定位之前有必要先了解清楚標準流和脫離標準流的特性
雖然浮動和定位很重要,但是在以後的網頁寫作中,還是盡量少用,最好別亂用,不然後
【BZOJ1004】Cards(組合數學,Burnside引理)
getchar 多次 等價 要求 std tdi cst 多少 存在 【BZOJ1004】Cards(組合數學,Burnside引理)
題面
Description
小春現在很清閑,面對書桌上的N張牌,他決定給每張染色,目前小春只有3種顏色:紅色,藍色,綠色.他詢問Su
監聽器[用於監聽ServletRequest對象的產生和銷毀] 學習筆記
監聽器[用於監聽ServletRequeimport javax.servlet.ServletRequestEvent;
import javax.servlet.ServletRequestListener;
//監聽器[用於監聽ServletRequest對象的產生和銷毀]
public class
監聽HttpSesison產生和銷毀 學習筆記
監聽HttpSesison產生和銷毀
import java.util.Date;
import javax.servlet.http.HttpSession;
import javax.servlet.http.HttpSessionEvent;
import javax.servlet.http.Htt
springmvc 日期轉換器和編碼過濾器 學習筆記
springmvc 日期轉換器和編碼過濾springmvc不能將String類型轉成Date類型,必須自定義類型轉換器
<!-- 編碼過濾器 -->
<filter>
<filter-name>CharacterEncodingFilter</
【Git和GitHub】學習筆記
不存在 lin AR 兩種 暫存區 mit 當前 jpg splay 1. 書籍推薦:
先看一本比較簡單並且好的入門書籍
Git - Book https://git-scm.com/book/zh/v2
2. 書籍理解:
Git 有三種狀態,你的文
Burnside引理與Polya定理
本質 left sum bsp 之間 染色 polya begin 兩個 感覺這兩個東西好鬼畜= = ,考場上出了肯定不會qwq。不過還是學一下吧用來裝逼也是極好的
群的定義
與下文知識無關。。
給出一個集合$G = \{a, b, c, \dots \}$和集合上的
【BZOJ3202】項鏈(莫比烏斯反演,Burnside引理)
相同 可能 urn cst i+1 arp com 最大 要求 【BZOJ3202】項鏈(莫比烏斯反演,Burnside引理)
題面
BZOJ
洛谷
題解
首先讀完題目,很明顯的感覺就是,分成了兩個部分計算。
首先計算本質不同的珠子個數,再計算本質不同的項鏈個數。
前面一個
burnside引理&polya定理
連接 集合 置換群 產生 side 交換 進行 置換 polya burnside引理&polya定理
置換:
置換即是將n個元素的染色進行交換,產生一個新的染色方案。
群:
一個元素的集合G與一個二元運算(*)構成一個群。群滿足一下性質:
封閉性:\(\fo
ML-提升方法和決策樹學習筆記
整合學習
整合學習通過構建並結合多個學習器來完成學習任務,有時也被稱為多分類器系統,基於委員會的學習。
同質整合:只包含同種型別的個體學習器。
異質整合:包含不同型別的個體學習器。
根據個體學習器的生成方式,目前的整合學習方法大致可分為兩大類,即個體學習器間存在強依賴關係,必須序
相關推薦
Burnside引理和polay計數學習筆記
首先提出一個問題,在一個2*2的矩陣裡染色,旋轉後相同算作一種,問有多少種染色方法。 顯然窮舉有那麼多種,然後發現,(3,4,5,6)是同一種,(7,8,9,10)是一種,(11,12)是一種,(13,14,15,16),1是一種,2是一種。 發
Burnside引理和Polya定理
開始 多少 tails 沒有 -s 圖片 detail 最簡 方案 轉載自:https://blog.csdn.net/whereisherofrom/article/details/79631703 Burnside引理 筆者第一次看到Burnside引理那個公式的時
【數學專題】(二) Burnside引理和Polya定理
Burnside引理 筆者第一次看到Burnside引理那個公式的時候一頭霧水,找了本組合數學的書一看,全是概念。後來慢慢從Polya定理開始,做了一些題總算理解了。本文將從最簡單的例子出發,解釋Burnside引理和Polya定理。然後提供一些自己做過的和上述定理相關的
Burnside引理和Polya定理之間的聯絡
最近,研究了兩天的Burnside定理和Polya之間的聯絡,百思不得其解,然後直到遇到下面的問題: 對顏色限制的染色 例:對正五邊形的三個頂點著紅色,對其餘的兩個頂點著藍色,問有多少種非等價的著色? 其中置換的方法有旋轉 \(0^{\circ}, 72^{\circ}, 144^{\circ}, 21
等價類計數(Polya定理/Burnside引理)學習筆記
參考:劉汝佳《演算法競賽入門經典訓練指南》 感覺是非常遠古的東西了,幾乎從來沒有看到過需要用這個的題,還是學一發以防翻車。 置換:排列的一一對映。置換乘法相當於函式複合。滿足結合律,不滿足交換律。 置換的迴圈分解:即將置換看成一張有向圖,分解成若干迴圈。迴圈的數量稱為迴圈節。 以置
[學習筆記]置換群 置換群和Burnside引理,Polya定理
這是群論。 置換群是群論的一種:必須要知道的: 置換群和Burnside引理,Polya定理 理解一下; 這裡置換就是旋轉同構的表示,方案就是“染色方案” m種置換,假如所有可能的方案,每種同構的方案都算了m次。(每種置換都有一次),那麼直接除以m即可。 但是有的方案並沒有被計
Burnside引理,Polya定理和一些計數問題(1)
變換 相同 不同的 觀察 本質 exist 關系 不變 陪集 Burnside引理 考慮一個$S$上的置換群$G$. 對於$u,v \in S$,定義它們“等價”當且僅當存在一個$G$中的置換,將$u$變為$v$.容易發現,這一關系是一個等價關系.設$E(k)$表示$k$所
置換群和Burnside引理,Polya定理
因子 不同的 mir details 構造 itl 置換群 模型 遇到 定義簡化版: 置換,就是一個1~n的排列,是一個1~n排列對1~n的映射 置換群,所有的置換的集合。 經常會遇到求本質不同的構造,如旋轉不同構,翻轉交換不同構等。 不動點:一個置換中,置換後和置換前沒有
burnside引理+polya計數法小結
WC上wwwwodddd講的整數和多項式相關裡面最後又burnside引理的一部分 被生成函式調戲瘋了的我突然斷線重連 坐在禮堂最後一排的沙發位上和老黃人瘋狂口糊 不過聽課的時候想的不是很細,重新整理了一發 大概就是 本質不同的方案數=1置換個
等價類計數:Burnside引理 & Polya定理
提示: 本文並非嚴謹的數學分析,有很多地方是自己瞎口胡的,僅供參考。有錯誤請不吝指出 :p ## 1. 群 ### 1.1 群的概念 群 $(S,\circ)$ 是一個元素集合 $S$ 和一種二元運算 $ \circ $ 的合稱,其滿足以下性質。 ##### 封閉性 >對於 $\forall a,b
網頁排版中的浮動和定位(學習筆記)
mage hidden alt images blog clear ul li -a www CSS中的浮動和定位 在了解CSS中的浮動和定位之前有必要先了解清楚標準流和脫離標準流的特性 雖然浮動和定位很重要,但是在以後的網頁寫作中,還是盡量少用,最好別亂用,不然後
【BZOJ1004】Cards(組合數學,Burnside引理)
getchar 多次 等價 要求 std tdi cst 多少 存在 【BZOJ1004】Cards(組合數學,Burnside引理) 題面 Description 小春現在很清閑,面對書桌上的N張牌,他決定給每張染色,目前小春只有3種顏色:紅色,藍色,綠色.他詢問Su
監聽器[用於監聽ServletRequest對象的產生和銷毀] 學習筆記
監聽器[用於監聽ServletRequeimport javax.servlet.ServletRequestEvent; import javax.servlet.ServletRequestListener; //監聽器[用於監聽ServletRequest對象的產生和銷毀] public class
監聽HttpSesison產生和銷毀 學習筆記
監聽HttpSesison產生和銷毀 import java.util.Date; import javax.servlet.http.HttpSession; import javax.servlet.http.HttpSessionEvent; import javax.servlet.http.Htt
springmvc 日期轉換器和編碼過濾器 學習筆記
springmvc 日期轉換器和編碼過濾springmvc不能將String類型轉成Date類型,必須自定義類型轉換器 <!-- 編碼過濾器 --> <filter> <filter-name>CharacterEncodingFilter</
【Git和GitHub】學習筆記
不存在 lin AR 兩種 暫存區 mit 當前 jpg splay 1. 書籍推薦: 先看一本比較簡單並且好的入門書籍 Git - Book https://git-scm.com/book/zh/v2 2. 書籍理解: Git 有三種狀態,你的文
Burnside引理與Polya定理
本質 left sum bsp 之間 染色 polya begin 兩個 感覺這兩個東西好鬼畜= = ,考場上出了肯定不會qwq。不過還是學一下吧用來裝逼也是極好的 群的定義 與下文知識無關。。 給出一個集合$G = \{a, b, c, \dots \}$和集合上的
【BZOJ3202】項鏈(莫比烏斯反演,Burnside引理)
相同 可能 urn cst i+1 arp com 最大 要求 【BZOJ3202】項鏈(莫比烏斯反演,Burnside引理) 題面 BZOJ 洛谷 題解 首先讀完題目,很明顯的感覺就是,分成了兩個部分計算。 首先計算本質不同的珠子個數,再計算本質不同的項鏈個數。 前面一個
burnside引理&polya定理
連接 集合 置換群 產生 side 交換 進行 置換 polya burnside引理&polya定理 置換: 置換即是將n個元素的染色進行交換,產生一個新的染色方案。 群: 一個元素的集合G與一個二元運算(*)構成一個群。群滿足一下性質: 封閉性:\(\fo
ML-提升方法和決策樹學習筆記
整合學習 整合學習通過構建並結合多個學習器來完成學習任務,有時也被稱為多分類器系統,基於委員會的學習。 同質整合:只包含同種型別的個體學習器。 異質整合:包含不同型別的個體學習器。 根據個體學習器的生成方式,目前的整合學習方法大致可分為兩大類,即個體學習器間存在強依賴關係,必須序