Burnside引理和Polya定理
阿新 • • 發佈：2018-05-31
開始 多少 tails 沒有 -s 圖片 detail 最簡 方案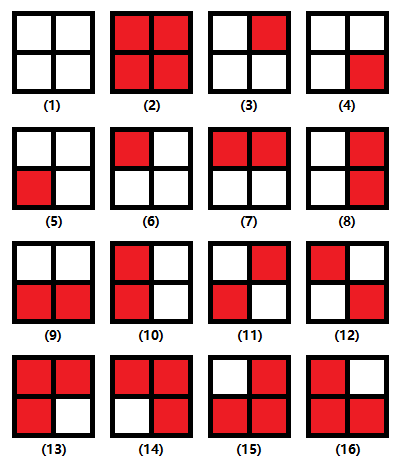 
圖1
將每種旋轉認為是一種"置換"，定義為gi，則上述問題總共有4種置換，分別描述為：
圖2
用D(gi)表示在gi這種"置換"的作用下沒有改變狀態的方案集合，則根據圖2易得：
圖3
用|D(gi)|代表集合D(gi)中元素的個數，則有Burnside引理表示如圖4所示：
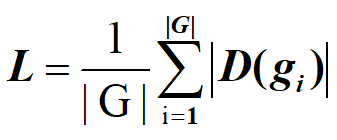圖4
L代表m種顏色給n個對象染色的總方案數，|G|代表置換個數，|D(gi)|代表在gi這種置換作用下沒有改變狀態的方案個數。
上文中的例子套用Burnside引理就是 L = (16+2+4+2)/4 = 6。
這道題幾乎是所有解釋Burnside引理的文章都會提到的一個例子，因為它看起來很直觀，然而當染色數或對象數逐漸增多時，方案數呈指數級增長，再來舉個例子。 
圖5
給每個格子編個號，每個格子有10種顏色，總共9個格子，總情況數10^9，已經沒辦法枚舉出來了。繼續從Burnside引理的定義出發，|D(gi)|代表在gi這種置換作用下沒有改變狀態的方案個數，置換總共四種，那麽我們將這四種置換都列出來：
1）旋轉0度：也就是我們將這個3×3的方格旋轉0度後，有多少種方案是沒有改變狀態的，答案很顯然，就是10^9。也就是說，無論你哪個格子染成什麽顏色都沒關系，旋轉0度前後狀態不變（這是顯然的）。
2）旋轉90度：①③⑦⑨循環變換、②④⑥⑧循環變換，⑤永遠不變。表示成置換群的乘積就是(1379)(2468)(5)。那麽我們發現，只要在同一個循環中的格子顏色一致，則在這種置換下狀態永遠不會改變。所以(1379)可以取10種顏色、(2468)可以取10種顏色、(5)可以取10種顏色，總方案數10^3。 
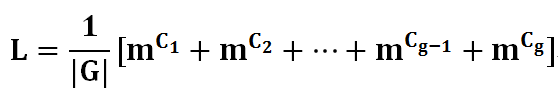圖6
m種顏色給n個對象染色的方案數如圖所示。G代表變換（置換）的種類，其中Ci代表每種置換下的循環節。
轉載自：https://blog.csdn.net/whereisherofrom/article/details/79631703
Burnside引理 筆者第一次看到Burnside引理那個公式的時候一頭霧水，找了本組合數學的書一看，全是概念。後來慢慢從Polya定理開始，做了一些題總算理解了。本文將從最簡單的例子出發，解釋Burnside引理和Polya定理。然後提供一些自己做過的和上述定理相關的題目和解題報告。 Burnside引理是為了解決m種顏色給n個對象染色的計數問題。 【例題1】如圖1所示，2×2方格中每個格子可以選擇染上2種顏色（紅色或白色）。那麽總共是2^4=16種情況。現在要問，如果旋轉0度、90度、180度、270度後狀態不變的方案算成同一種方案，問總共有多少種不同的方案。
圖1
將每種旋轉認為是一種"置換"，定義為gi，則上述問題總共有4種置換，分別描述為：
圖2
用D(gi)表示在gi這種"置換"的作用下沒有改變狀態的方案集合，則根據圖2易得：
圖3
用|D(gi)|代表集合D(gi)中元素的個數，則有Burnside引理表示如圖4所示：
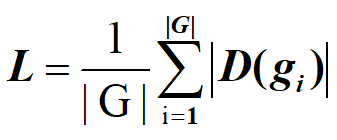圖4
L代表m種顏色給n個對象染色的總方案數，|G|代表置換個數，|D(gi)|代表在gi這種置換作用下沒有改變狀態的方案個數。
上文中的例子套用Burnside引理就是 L = (16+2+4+2)/4 = 6。
這道題幾乎是所有解釋Burnside引理的文章都會提到的一個例子，因為它看起來很直觀，然而當染色數或對象數逐漸增多時，方案數呈指數級增長，再來舉個例子。
圖5
給每個格子編個號，每個格子有10種顏色，總共9個格子，總情況數10^9，已經沒辦法枚舉出來了。繼續從Burnside引理的定義出發，|D(gi)|代表在gi這種置換作用下沒有改變狀態的方案個數，置換總共四種，那麽我們將這四種置換都列出來：
1）旋轉0度：也就是我們將這個3×3的方格旋轉0度後，有多少種方案是沒有改變狀態的，答案很顯然，就是10^9。也就是說，無論你哪個格子染成什麽顏色都沒關系，旋轉0度前後狀態不變（這是顯然的）。
2）旋轉90度：①③⑦⑨循環變換、②④⑥⑧循環變換，⑤永遠不變。表示成置換群的乘積就是(1379)(2468)(5)。那麽我們發現，只要在同一個循環中的格子顏色一致，則在這種置換下狀態永遠不會改變。所以(1379)可以取10種顏色、(2468)可以取10種顏色、(5)可以取10種顏色，總方案數10^3。
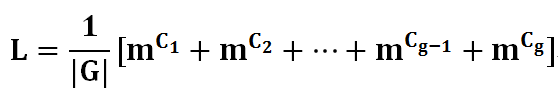圖6
m種顏色給n個對象染色的方案數如圖所示。G代表變換（置換）的種類，其中Ci代表每種置換下的循環節。Burnside引理和Polya定理