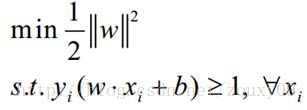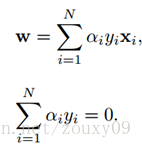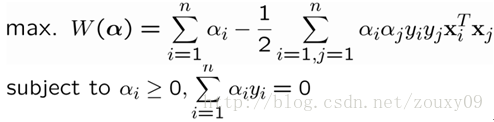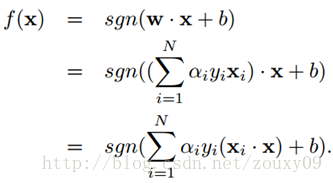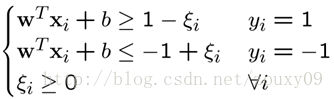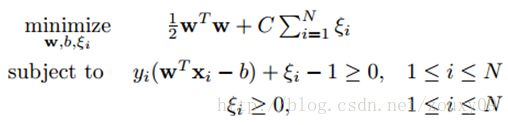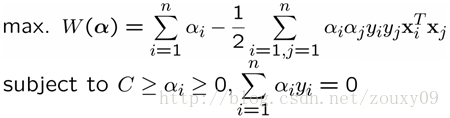許多地方得SVM講得都很晦澀，不容易理解，最近看到一篇不錯的博文寫得很好，同時加上自己的理解，重新梳理一下知識要點

http://blog.csdn.net/zouxy09/article/details/17291543

一、引入

SVM是個分類器。我們知道，分類的目的是學會一個分類函式或分類模型（或者叫做分類器），該模型能把資料庫中的資料項對映到給定類別中的某一個，從而可以用於預測未知類別。

對於用於分類的支援向量機，它是個二分類的分類模型。也就是說，給定一個包含正例和反例（正樣本點和負樣本點）的樣本集合，支援向量機的目的是尋找一個超平面來對樣本進行分割，把樣本中的正例和反例用超平面分開，但是不是簡單地分看，其原則是使正例和反例之間的間隔最大。學習的目標是在特徵空間中找到一個分類超平面wx+b=0，分類面由法向量w和截距b決定。分類超平面將特徵空間劃分兩部分，一部分是正類，一部分是負類。法向量指向的一側是正類，另一側為負類。這裡有兩點需要注意，類別為（+1，-1）而之前的邏輯迴歸演算法中多為（+1,0）這裡沒有什麼特別的原因，主要是計算的方便，還有超平面沒有限制多少維，只要比資料維度低一維就可以了。

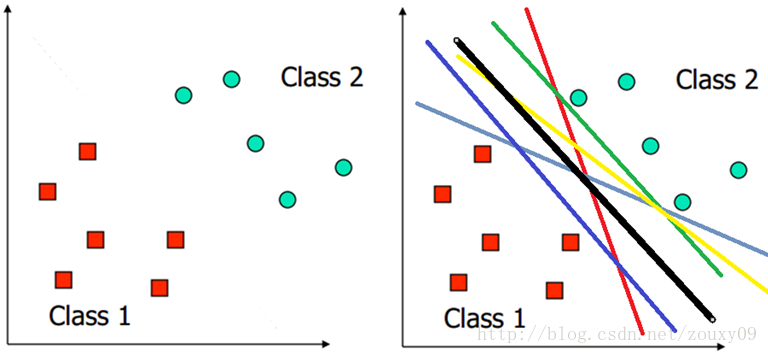
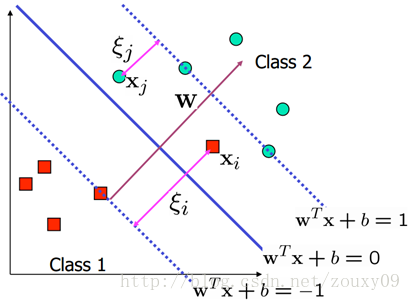
先給出一個簡單的例子：

二、線性可分SVM與硬間隔最大化

SVM試圖尋找一個超平面來對樣本進行分割，把樣本中的正例和反例用超平面分開，但是不是很敷衍地簡單的分開，而是盡最大的努力使正例和反例之間的間隔margin最大。這樣它的分類結果才更加可信，而且對於未知的新樣本才有很好的分類預測能力

  我們的目標是尋找一個超平面，使得離超平面比較近的點能有更大的間距。也就是我們不考慮所有的點都必須遠離超平面，我們關心求得的超平面能夠讓所有點中離它最近的點具有最大間距。而距離超平面最近的點就是支援向量

      假設我們有N個訓練樣本{(x

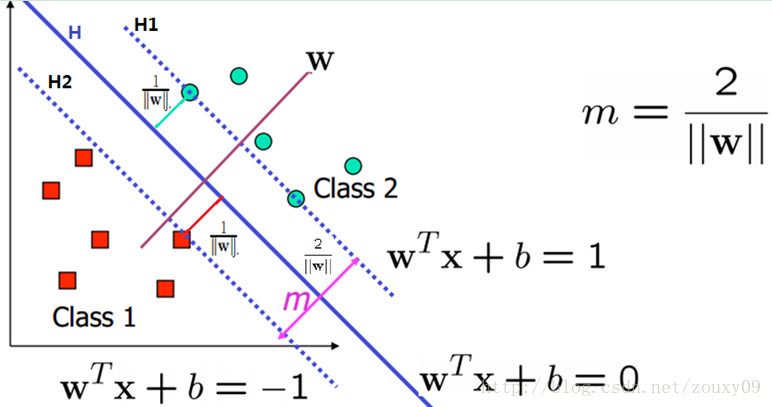
      這裡我們需要用這些樣本去訓練學習一個線性分類器（超平面）：f(x)=sgn(w^Tx + b)，也就是w^Tx + b大於0的時候，輸出+1，小於0的時候，輸出-1。sgn()表示取符號。而g(x) =w^Tx + b=0就是我們要尋找的分類超平面，如上圖所示。剛才說我們要怎麼做了？我們需要這個超平面最大的分隔這兩類。也就是這個分類面到這兩個類的最近的那個樣本的距離相同，而且最大。為了更好的說明，我們在上圖中找到兩個和這個超平面平行和距離相等的超平面：H₁

       好了，這時候我們就需要兩個條件：（1）沒有任何樣本在這兩個平面之間；（2）這兩個平面的距離需要最大。（對任何的H₁和H₂，我們都可以歸一化係數向量w，這樣就可以得到H₁和H₂表示式的右邊分別是+1和-1了）。

先來看條件（2）。我們需要最大化這個距離，所以就存在一些樣本處於這兩條線上，他們叫支援向量（後面會說到他們的重要性）。那麼它的距離是什麼呢，兩條平行線的距離的求法，例如ax+by=c1和ax+by=c2，那他們的距離是|c2-c1|/sqrt(x²+y²)（sqrt()表示開根號）。注意的是，這裡的x和y都表示二維座標。而用w來表示就是H₁:w₁x₁+w₂x₂=+1和H₂:w₁x₁+w₂x₂=-1，那H₁和H₂的距離就是|1+1|/ sqrt(w₁²+w₁²)=2/||w||。也就是w的模的倒數的兩倍。也就是說，我們需要最大化margin=2/||w||，為了最大化這個距離，我們應該最小化||w||，看起來好簡單哦。同時我們還需要滿足條件（1），也就是同時要滿足沒有資料點分佈在H₁和H₂之間：

      也就是，對於任何一個正樣本y_i=+1，它都要處於H₁的右邊，也就是要保證：y= w^Tx+ b>=+1。對於任何一個負樣本y_i=-1，它都要處於H₂的左邊，也就是要保證：y = w^Tx + b<=-1。這兩個約束，其實可以合併成同一個式子：y_i (w^Tx_i + b)>=1。（這裡解釋了為什麼樣本為+1，-1）

      所以我們的問題就變成：

兩個式子分別表示了，最大化支援向量與超平面的距離，在支援平面+1，-1區域內沒有樣本點

下面就進入帶約束條件的最優化問題了

這是個凸二次規劃問題。什麼叫凸？凸集是指有這麼一個點的集合，其中任取兩個點連一條直線，這條線上的點仍然在這個集合內部，因此說“凸”是很形象的。例如下圖，對於凸函式（在數學表示上，滿足約束條件是仿射函式，也就是線性的Ax+b的形式）來說，區域性最優就是全域性最優，但對非凸函式來說就不是了。二次表示目標函式是自變數的二次函式。

      好了，既然是凸二次規劃問題，就可以通過一些現成的 QP (Quadratic Programming) 的優化工具來得到最優解。所以，我們的問題到此為止就算全部解決了。雖然這個問題確實是一個標準的 QP 問題，但是它也有它的特殊結構，通過 Lagrange Duality 變換到對偶變數 (dual variable) 的優化問題之後，可以找到一種更加有效的方法來進行求解，而且通常情況下這種方法比直接使用通用的 QP 優化包進行優化要高效得多。也就說，除了用解決QP問題的常規方法之外，還可以應用拉格朗日對偶性，通過求解對偶問題得到最優解，這就是線性可分條件下支援向量機的對偶演算法，這樣做的優點在於：一是對偶問題往往更容易求解；二者可以自然的引入核函式，進而推廣到非線性分類問題。

先簡單地說核函式的一個作用就是可以將一個低維的非線性資料對映成為高維的線性資料

三、Dual優化問題

3.1、對偶問題

       在約束最優化問題中，常常利用拉格朗日對偶性將原始問題轉換為對偶問題，通過求解對偶問題而得到原始問題的解。至於這其中的原理和推導參考文獻[3]講得非常好。大家可以參考下。這裡只將對偶問題是怎麼操作的。假設我們的優化問題是：

min f(x)

s.t. h_i(x) = 0, i=1, 2, …,n

       這是個帶等式約束的優化問題。我們引入拉格朗日乘子，得到拉格朗日函式為：

L(x, α)=f(x)+α₁h₁(x)+ α₂h₂(x)+…+α_nh_n(x)  

（拉格朗日函式將約束條件融入到表示式中，方便之後的處理）

       然後我們將拉格朗日函式對x求極值，也就是對x求導，導數為0，就可以得到α關於x的函式，然後再代入拉格朗日函式就變成：

max W(α) = L(x(α), α)

       這時候，帶等式約束的優化問題就變成只有一個變數α（多個約束條件就是向量）的優化問題，這時候的求解就很簡單了。同樣是求導另其等於0，解出α即可。需要注意的是，我們把原始的問題叫做primal problem，轉換後的形式叫做dual problem。需要注意的是，原始問題是最小化，轉化為對偶問題後就變成了求最大值了。對於不等式約束，其實是同樣的操作。簡單地來說，通過給每一個約束條件加上一個 Lagrange multiplier（拉格朗日乘子），我們可以將約束條件融和到目標函式裡去，這樣求解優化問題就會更加容易。（這裡其實涉及到很多蠻有趣的東西的，大家可以參考更多的博文）

3.2、SVM優化的對偶問題

       對於SVM，前面提到，其primal problem是以下形式：

       同樣的方法引入拉格朗日乘子，我們就可以得到以下拉格朗日函式：

（這裡感覺應該是+b寫錯了）

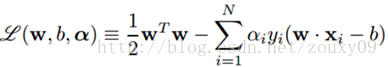
  然後對L(w, b, α)分別求w和b的極值。也就是L(w, b,α)對w和b的梯度為0：∂L/∂w=0和∂L/∂b=0，還需要滿足α>=0。求解這裡導數為0的式子可以得到：

       然後再代入拉格朗日函式後，就變成：

        這個就是dual problem（如果我們知道α，我們就知道了w。反過來，如果我們知道w，也可以知道α）。這時候我們就變成了求對α的極大，即是關於對偶變數α的優化問題（沒有了變數w，b，只有α）。當求解得到最優的α*後，就可以同樣代入到上面的公式，匯出w*和b*了，最終得出分離超平面和分類決策函式。也就是訓練好了SVM。那來一個新的樣本x後，就可以這樣分類了：

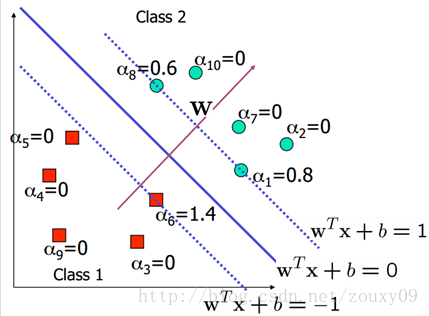
       在這裡，其實很多的α_i都是0，也就是說w只是一些少量樣本的線性加權值。這種“稀疏”的表示實際上看成是KNN的資料壓縮的版本。也就是說，以後新來的要分類的樣本首先根據w和b做一次線性運算，然後看求的結果是大於0還是小於0來判斷正例還是負例。現在有了α_i，我們不需要求出w，只需將新來的樣本和訓練資料中的所有樣本做內積和即可。那有人會說，與前面所有的樣本都做運算是不是太耗時了？其實不然，我們從KKT條件中得到，只有支援向量的α_i不為0，其他情況α_i都是0。因此，我們只需求新來的樣本和支援向量的內積，然後運算即可。這種寫法為下面要提到的核函式（kernel）做了很好的鋪墊。如下圖所示：

四、鬆弛向量與軟間隔最大化（Good）

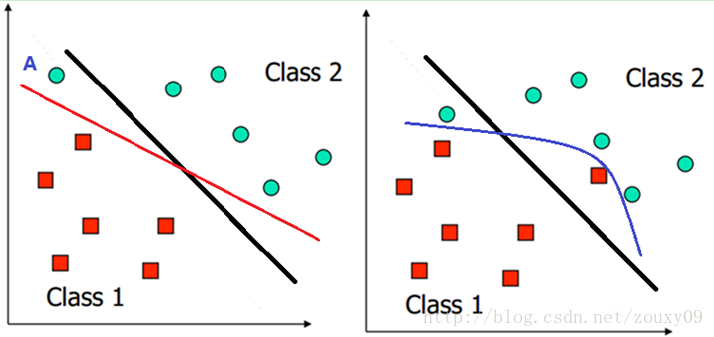
       我們之前討論的情況都是建立在樣本的分佈比較優雅和線性可分的假設上，在這種情況下可以找到近乎完美的超平面對兩類樣本進行分離。但如果遇到下面這兩種情況呢？左圖，負類的一個樣本點A不太合群，跑到正類這邊了，這時候如果按上面的確定分類面的方法，那麼就會得到左圖中紅色這條分類邊界，嗯，看起來不太爽，好像全世界都在將就A一樣。還有就是遇到右圖的這種情況。正類的一個點和負類的一個點都跑到了別人家門口，這時候就找不到一條直線來將他們分開了，那這時候怎麼辦呢？我們真的要對這些零丁的不太聽話的離群點屈服和將就嗎？就因為他們的不完美改變我們原來完美的分介面會不會得不償失呢？但又不得不考慮他們，那怎樣才能折中呢？

       對於上面說的這種偏離正常位置很遠的資料點，我們稱之為 outlier，它有可能是採集訓練樣本的時候的噪聲，也有可能是某個標資料的大叔打瞌睡標錯了，把正樣本標成負樣本了。那一般來說，如果我們直接忽略它，原來的分隔超平面還是挺好的，但是由於這個 outlier 的出現，導致分隔超平面不得不被擠歪了，同時 margin 也相應變小了。當然，更嚴重的情況是，如果出現右圖的這種outlier，我們將無法構造出能將資料線性分開的超平面來。

      為了處理這種情況，我們允許資料點在一定程度上偏離超平面。也就是允許一些點跑到H₁和H₂之間，也就是他們到分類面的間隔會小於1。如下圖：

ξ_{i : 引入的鬆弛因子，就是允許樣本點在超平面之間的一些相對偏移}

_{C：懲罰因子：如果有一定得偏移量，那麼將這個因子加到拉格朗日的式子當中，在求||w||最小值的計算當中增加懲罰}

       具體來說，原來的約束條件就變為：

        這時候，我們在目標函式裡面增加一個懲罰項，新的模型就變成（也稱軟間隔）：

       引入非負引數ξ_i後（稱為鬆弛變數），就允許某些樣本點的函式間隔小於1，即在最大間隔區間裡面，或者函式間隔是負數，即樣本點在對方的區域中。而放鬆限制條件後，我們需要重新調整目標函式，以對離群點進行處罰，目標函式後面加上的第二項就表示離群點越多，目標函式值越大，而我們要求的是儘可能小的目標函式值。這裡的C是離群點的權重，C越大表明離群點對目標函式影響越大，也就是越不希望看到離群點。這時候，間隔也會很小。我們看到，目標函式控制了離群點的數目和程度，使大部分樣本點仍然遵守限制條件。

        這時候，經過同樣的推導過程，我們的對偶優化問題變成：

       此時，我們發現沒有了引數ξ_i，與之前模型唯一不同在於α_i又多了α_i<=C的限制條件。需要提醒的是，b的求值公式也發生了改變，改變結果在SMO演算法裡面介紹。