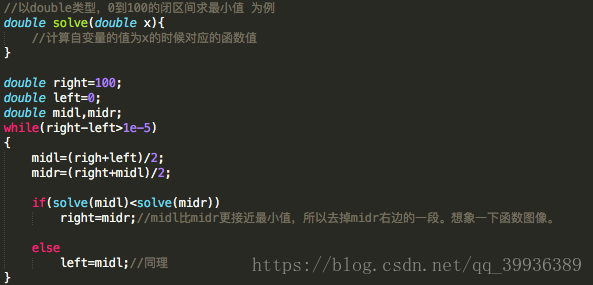
與二分查詢類似的三分搜尋
原理什麼的都是相同的,三分搜尋也是基於分治思想的查詢演算法。
但是我們仔細想想二分查詢,是不是隻適合單調函式。
而三分搜尋可以用於凸函式和凹函式。
三分搜尋同樣有left和right,但是中點不再是一個mid,而是兩個
midl=(left+right)/2; midr=(midl+right)/2;
因此可以判斷出兩個中點相對於函式極值的位置
懶得畫圖了,直接拿網上的一個圖來解釋一下。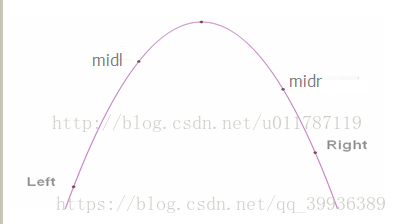
我的理解是當要求一個凸函式或者凹函式的極值時,可以使用三分搜尋。
下面是三分搜尋的模板
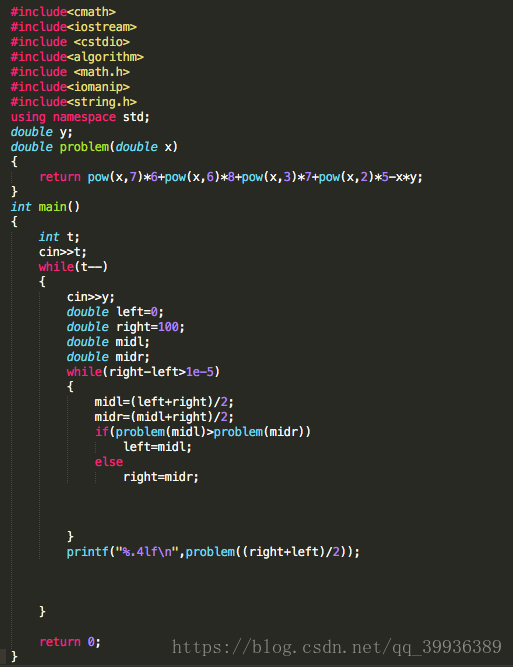
下面是一個三分的例題。
ac程式碼:
還是模板題
要掌握還是要多加練習,模板題只是入個門。
二分三分也經常是用來結合別的演算法一起解題。
//人一我十,人十我百。
相關推薦
與二分查詢類似的三分搜尋
原理什麼的都是相同的,三分搜尋也是基於分治思想的查詢演算法。 但是我們仔細想想二分查詢,是不是隻適合單調函式。 而三分搜尋可以用於凸函式和凹函式。 三分搜尋同樣有left和right,但是中點不再是一個mid,而是兩個 midl=(left+right)
查詢-二分查詢、三分查詢
二分查詢的查詢過程是: 每輪與有序區間的中間元素進行比較,若相等則返回當前元素位置。若被查詢元素大於中間元素,則到右側區間查詢,若查詢元素小於中間元素,則到左側區間查詢。 不斷重複前序查詢過程,或者待查詢區間失效。 輸入:表的長度,表中各個元素。要查詢的表元素。 輸出
三分搜尋 (演算法設計與分析課後習題)
三分搜尋演算法的做法是:它先將待查元素x與n/3處的元素比較,然後將x與2n/3處的元素進行比較。比較的結果或者找到x,或者將搜尋範圍縮小的原來的n/3 1)編寫C++程式實踐演算法 2)分析演算法的時間複雜度 1) #include <cstdio> in
codeforces D. Nature Reserve(三分搜尋+公式)最小圓覆蓋問題
轉載自https://blog.csdn.net/qq_38891827/article/details/82965187 題意 給你一些二維平面上的點,找一個與x軸相切的半徑最小的圓包含所有點。 做法 首先如果兩邊都有點的情況一定是找不到這樣的圓的,否則一定可以找到這樣的圓首先如果
STL之find與二分查詢
要使用find()函式需包含algorithm標頭檔案。 template <class InputIterator, class T> InputIterator find (InputIterator first, InputIterator last, const T&
三分搜尋
目錄 一、概念 二、演算法過程 三、程式碼 轉自:https://blog.csdn.net/u011787119/article/details/44598871 https://www.cnblogs.com/ECJTUACM-873284962/p/6536414.ht
遞迴函式與二分查詢演算法
一、遞迴函式 1.遞迴呼叫的定義 遞迴呼叫是函式巢狀呼叫的一種特殊形式,函式在呼叫時,直接或間接呼叫了自身,就是遞迴呼叫 def foo(n): print(n) n += 1 foo(n) foo(1) 2.遞迴最大深度 最大遞迴深度預設是
PTA|01-複雜度3 二分查詢 (20 分)二分查詢
本題要求實現二分查詢演算法。 函式介面定義: Position BinarySearch( List L, ElementType X ); 其中List結構定義如下: typedef int Position; typedef struct LNode *L
1-8 二分查詢 (20 分)
本題要求實現二分查詢演算法。 函式介面定義: Position BinarySearch( List L, ElementType X ); 其中List結構定義如下: typedef int Position; typedef struct LNode *List; struct
01-複雜度3 二分查詢 (20 分)
本題要求實現二分查詢演算法。 函式介面定義: Position BinarySearch( List L, ElementType X ); 其中List結構定義如下: typedef int
ACM-三分搜尋
類似於二分查詢,三分搜尋法也是比較常用的基於分治思想的高效查詢方法。但是和二分不同,二分只適用於單調函式,比如常用的對單調遞增或單調遞減的一個序列中的某一個元素進行查詢,三分卻突破了這種限制,可以用於左邊遞增右邊遞減或者相反的,這麼一類函式,也就是常說的凸函式和凹函式。但是
[搜尋演算法]三分搜尋初步
前言 對於單調函式,如果找到了其單調性,我們就可以使用二分的方法對其進行搜尋。所以二分搜尋的首要前提是具有單調性。當搜尋的函式不具有單調性時,二分搜尋就顯得相形見絀了。所以對於較為複雜的函式,我們可以採用三分搜尋和模擬退火的方法。這裡主要來分析一下三分搜
01-複雜度3 二分查詢(20 分)
本題要求實現二分查詢演算法。 函式介面定義: Position BinarySearch( List L, ElementType X ); 其中List結構定義如下: typedef int Position; typedef struct LNod
Python實現素數篩法與二分查詢(遞迴)
def prime(n): if n<=2: return [] result=[False,False]+[True]*(n-2) for i in range(len(result)): if result[
HBU月考 二分查詢(20分)
題目描述: 利用二分查詢找出所給出的數在陣列中的下標。 輸入格式: 第一行輸入n和m表示陣列有n個數據,m表示要對m個數進行查詢。 輸出格式: 所有輸出在一行完成,行末沒有多餘空格和多餘回車。 輸入樣例: 5 5 1 2 3 4 5 1 2 3 4 5 輸出樣例:
PTA 01-複雜度3 二分查詢 (20 分)
01-複雜度3 二分查詢 (20 分) 本題要求實現二分查詢演算法。 函式介面定義: Position BinarySearch( List L, ElementType X ); 其中List結構定義如下: typedef int Position; typedef
poj3737(三分搜尋)
題意:給出一個圓錐的表面積(側面積+底面積),求圓錐的最大體積。 解法:三分半徑。左邊界隨便取個極小的數,右邊界可以假定這個圓錐是平的,高是0.這是底面積的二倍是表面積。 程式碼: /*******************************************
三分搜尋——初見
三分搜尋把區間分成3段,用來查詢最值。 二分演算法需要原來的區間是順序排列的,三分搜尋需要區間是凸函式! 如:搜尋區間為l~r,則中間2個點為 l+(r-l)/3 = (2l+r)/3 和 r-(r-l)/3 = (2r+l)/3。將整個區間分為了3段。然後就進行對比。縮
python-線性查詢與二分查詢
線性查詢 線性查詢就是從頭到尾,直到符合條件了就返回。比如在一個list中找到一個等於5的元素並返回下標: number_list = [0,1,2,3,4,5,6,7] ''' enumerate()函式用於將一個可遍歷的資料物件(如列表、
三分搜尋總結
一、概念: 一看三分便知道和是由二分演變而來,二分一般求單調區間的情況,而三分適合求凹凸函式,通常用來確定最值,三分是在二分基礎上將右區間再分為兩個區間。 二、演算法步驟: (1)先取整個區間的中間值 mid = (x+y)/ 2 ; (2)再將右區間