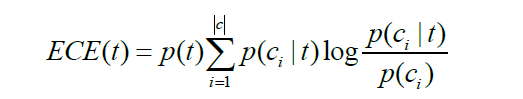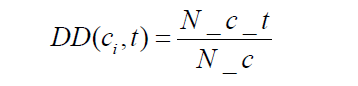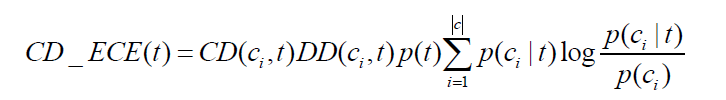本文轉自：http://blog.csdn.net/fighting_one_piece/article/details/38562183

期望交叉熵也稱為KL距離，反映的是文字類別的概率分佈和在出現了某個特徵的條件下文字類別的概率分佈之間的距離，具體公式表示如下

其中， P(t)表示特徵t在文字中出現的概率， P(ci)表示ci類文字在文字集中出現的概率， P(ci|t)表示文字包含特徵t時屬於類別c的概率，|c|表示類別總數。如果特徵t和類別強相關，即P(ci|t)大，並且相應的P(ci)又比較小，則說明特徵t對分類的影響大，相應的期望交叉熵值也較大，特徵在特徵子集中的排名就會比較靠前。

期望交叉熵在文字分類的特徵選擇中得到了廣泛的應用，並且取得了很好的效果，與資訊增益相比，期望交叉熵不再考慮特徵項不出現的情

特徵項在類內和類間分佈的均勻程度與它對分類的影響有以下兩方面的關係： 

1) 若存在某個特徵詞，該特徵詞如果集中地出現在某個類別中，而在其他類別中很少出現，那麼這個特徵詞就可以很好的將其所在的類別和其他類別區分，就可以很好的代表當前類別，對分類的貢獻也就越大。 
2) 若存在某個特徵詞，在其當前所在類別中，如果含有該特徵詞的文字數在該類別中所佔的比例越高，就越能代表當前類別，對分類的貢獻也就越大。 
為了描述以上兩方面的關係，本文引入了特徵項的類間集中度和類內分散度兩個概念。

類間集中度(Concentration Degree)：表示的是特徵項在各個類別中分佈的均勻程度，特徵項越集中分佈在某個類別中而不是均勻分佈在各個類中時，帶有的類別資訊就越多，表徵類別的能力就越強。計算公式如下：

其中，N_c_t表示ci類中出現特徵t的文字數，N_t表示訓練集中出現t的文字數。

類內分散度(Distribution Degree)：表示的是特徵項在某個類內部分佈的均勻程度，特徵 項在某個類中越多的文字中出現，越分散，就越能代表該類，對分類的貢獻越大。計算公式如下：

其中，N_c_t 表示ci類中出現特徵t的文字數，N_c 表示ci類中的總文字數。

特徵項的類間集中度和類內分散度是需要綜合考慮的，兩者缺一不可。如果只考慮二者其一，得到的特徵項就不能很好地提高分類效果，不僅不能提高期望交叉熵的特徵選擇效果，還會對特徵選擇造成干擾。例如：假設有三個類別，每個類別有100篇文字，若某個特徵詞只在其中一個類別中出現了1次，該特徵詞明顯是一個稀有特徵詞，不能很好地代表該類的資訊，是應該在特徵選擇中被淘汰的，但如果只考慮類間集中度，則該特徵項的類間集中度為100%，特徵選擇

由公式可見，在基於類間集中度和類內分散度的期望交叉熵中，特徵項在傳統期望交叉熵基礎上，若類間集中度越高，類內分散度越高，得到的特徵分數就越高，就越有可能被選入特徵子集。