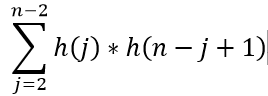卡特蘭數又稱卡塔蘭數，英文名Catalan number，是組合數學中一個常出現在各種計數問題中出現的數列。以比利時的數學家歐仁·查理·卡塔蘭 (1814–1894)的名字來命名。

最初，給卡塔蘭數建立的數學模型是：一個凸n邊形，通過不相交於n邊形內部的對角線，把n邊形拆分成若干三角形，不同的拆分數目用h_n表示，h_n即為Catalan數。例如五邊形有如下五種拆分方案(如圖)，故h₅=5。求對於一個任意的凸n邊形相應的h_n。

輸入一個正整數n，代表凸n邊形的邊數 (2≤n≤37)輸出一個正整數，凸n邊形劃分成若干三角形的不同劃分方式

樣例輸入

樣例輸入一：4
樣例輸入二：5

樣例輸出一：2
樣例輸出二：5

找出遞推式，三角形可認為是獨立的1種拆分方式

解題思路

    你可以百度一下什麼是卡特蘭數（據說卡特蘭是通過找到凸n邊形劃分成若干三角形的不同劃分方式的規律發現了卡特蘭數，忽略這句話），接下來我回來引導你找到這個遞推規律。

    首先，畫一個凸n邊形（我不可能真的給你畫一個n邊形吧？），如下圖所示

    如上圖所示，我畫了一個凸n邊形，我設凸n邊形的不同劃分方式為h(n)種。給凸n邊形的每一個角都編上號，從1到n。現在固定住1和n角，在其它頂點上任意選一個頂點j，連線1、j和n、j，發現把這個凸n邊形分成了三個形狀，第一個是一個j邊形，第二個是一個三角形，第三個是一個n-j+1邊形。我們知道j邊形有h(j)

#include<iostream>
using namespace std;
long long h[40];//要用long long型，要不然會爆
int main()
{
	int i,j,n;
	h[0]=1,h[1]=1;h[2]=1;//初始值設定好
	cin>>n;
	for(i=3;i<=n;i++)//
		for(j=2;j<=i-1;j++)//j從2到n
			h[i]+=h[j]*h[i-j+1];//遞推公式
	h[2]=0;//沒有2邊形，把h[2]置為0
	cout<<h[n];
	return 0;
}