拉格朗日乘子法與KKT條件
1. 一般約束優化問題
一般約束優化問題的形式為：
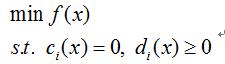定義拉格朗日函式為：
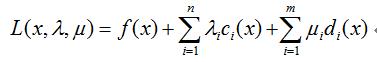則一般約束優化問題的最優性條件（KKT條件）：
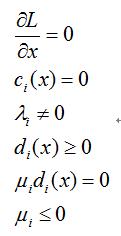2. 對偶問題
一個優化問題可以從兩個角度來考慮，一是被優化的原問題，其次是基於拉格朗日函式定義的對偶問題，也即極大極小問題：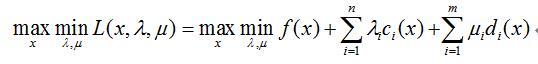
為什麼上式是對偶問題：
1. 一般約束優化問題，完全等價於下式：
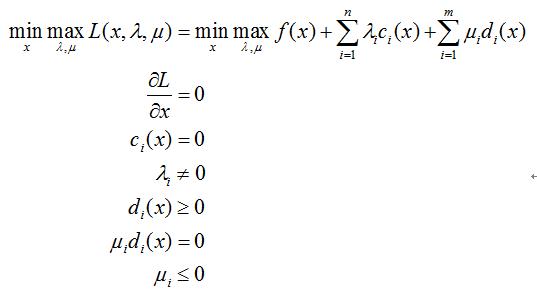2. 極小極大小於等於極大極小：
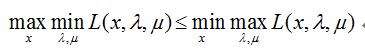3. 等號成立的條件（大概是這樣）1）原函式為凸函式， 為凸函式。
2）KKT條件成立
相關推薦
約束優化方法之拉格朗日乘子法與KKT條件
引言 本篇文章將詳解帶有約束條件的最優化問題，約束條件分為等式約束與不等式約束，對於等式約束的優化問題，可以直接應用拉格朗日乘子法去求取最優值；對於含有不等式約束的優化問題，可以轉化為在滿足 KKT 約束條件下應用拉格朗日乘子法求解。拉格朗日求得的並不一定是最優解，只有在凸
拉格朗日乘子法與KKT條件
1. 一般約束優化問題 一般約束優化問題的形式為： 定義拉格朗日函式為： 則一般約束優化問題的最優性條件（KKT條件）： 2. 對偶問題 一個優化問題可以從兩個角度來考慮，一是被優化的原
SVM演算法（深入理解拉格朗日乘子法與KKT條件的證明）
SVM應該是一個應用到數學知識很多的AI演算法，關於KKT的證明花了很長時間，裡面涉及到大量線性代數的知識。 對偶關係、方向導數與梯度的關係、梯度方向與構造的可取區域的關係、拉格朗日乘子引入的真實含義等等。 （一）間隔與支援向量 SVM（support vector
對拉格朗日乘子法與KKT的理解
在求解最優化問題中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）條件是兩種最常用的方法。在有等式約束時使用拉格朗日乘子法，在有不等約束時使用KKT條件。 我們這裡提到的最優化問題通常是指對於給定的某一函式，求其在指定作用域上的全域性
約束極值問題：拉格朗日乘子法、KKT條件與對偶理論
1 等式約束極值問題 考慮非線性規劃 minf(x)x∈Rns.t.φi(x)=0,i=1,⋯ ,m\begin{aligned} \min &\quad f(\bm{x}) \quad \bm{x}\in\R^
拉格朗日乘子法和KKT條件
數值 想象 radi 如果 ont inf 解決 tex spa 1. 拉格朗日乘子(Lagrange Multiplier)法 假設函數z=f(x,y)，求該函數的最小值，如果沒有約束條件，則可以表示為minf(x,y)，要求出minf(x,y)很簡單，根據Fermat
拉格朗日乘子法及KKT條件證明
一、簡介 在取有約束條件的優化問題時，拉格朗日乘子法（Lagrange Multiplier) 和KKT條件是非常重要的兩個求取方法，對於等式約束的優化問題，可以應用拉格朗日乘子法去求取最優值；如果含有不等式約束，可以應用KKT條件去求取。當然，這兩個方法求得的結果只是必要條件，只有
真正理解拉格朗日乘子法和KKT條件
這篇博文中直觀上講解了拉格朗日乘子法和 KKT 條件，對偶問題等內容。 首先從無約束的優化問題講起，一般就是要使一個表示式取到最小值： minf(x)minf(x) 如果問題是 maxf(x)maxf(x) 也可以通過取反轉化為求最小值min−f(x
解密SVM系列（一）：關於拉格朗日乘子法和KKT條件
寫在之前 支援向量機（SVM），一個神祕而眾知的名字，在其出來就受到了莫大的追捧，號稱最優秀的分類演算法之一，以其簡單的理論構造了複雜的演算法，又以其簡單的用法實現了複雜的問題，不得不說確實完美。 本系列旨在以基礎化的過程，例項化的形式一探S
【機器學習之數學】03 有約束的非線性優化問題——拉格朗日乘子法、KKT條件、投影法
目錄 將有約束問題轉化為無約束問題 拉格朗日法 KKT條件 拉格朗日法更新方程 凸優化問題下的拉格朗日法 罰函式法 對梯度演
機器學習 --- 拉格朗日乘子法和KTT條件
本篇文章主要為之後的支援向量機打下數學基礎 一、拉格朗日乘子法的目的 拉格朗日乘子法將原始的約束問題轉換成求解無約束優化問題。 對形如： 通過拉格朗日乘子法轉化成： 通俗地說就是轉換目標函式，把約束條件去掉。
拉格朗日乘子法的幾何解釋
font nbsp 幾何 lam 極值 而在 相交 排除 最大 問題：函數f(x,y,z)在 g(x,y,z)=0 的約束下取極值（最大或最小) f(x,y,z)=c c取定義域中的任意值時形成空間中一系列曲面 S_f，這些曲面互相平行（不允許相交--等位面|線
深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT條件
比較 log lan 條件 出了 net csdn art blank 這篇將拉格朗日函數比較全面，其中明確給出了拉格朗日函數，拉格朗日乘子的定義 深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT條件深入理解拉格朗日乘子法（Lagrange Mu
最優化問題求解之拉格朗日乘子法+KKT條件
因SVM-- 拉格朗日對偶（Lagrange duality）問題而學習 https://blog.csdn.net/u011067360/article/details/25215465 這篇博文不錯，整理了筆記，順便收藏在這 KKT條件：對一般的任意問題而言，是使一組解成為最優解
【機器學習筆記16】拉格朗日乘子法
【參考資料】 【1】《統計學習方法》 【2】《凸優化》 【3】小象學院 《凸優化》 凸集 直線和線段的表達 設x1≠x2x_1 \ne x_2x1̸=x2是RnR^nRn空間上的兩個點，具有存在下列定義的點： y=θx1+(1−θ)x2y = \thet
拉格朗日乘子法（有約束優化問題）
拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)條件是求解約束優化問題的重要方法，在有等式約束時使用拉格朗日乘子法，在有不等約束時使用KKT條件。前提是：只有當目標函式為凸函式時，使用這兩種方法才保證求得的是最優
數學基礎-拉格朗日乘子法學習資料
最近學習支援SVM，其中目標函式是一個有約束條件下的最優化問題。 這個問題要用拉格朗日乘子法進行推導。個人本來打算寫一篇文章來解釋這個。後來通過查詢，發現網上有很多資料，把這些讀了一遍，發現疑問都解決了。所以在這裡把資料彙總一下，與大家分享。 學習資料 數學掃盲----拉格朗日乘子法 拉
機器學習數學原理（5）——廣泛拉格朗日乘子法
機器學習數學原理（5）——廣泛拉格朗日乘子法 這一篇部落格針對的是有約束的凸優化問題，主要是為後面的最優間隔分類器以及其演化的SVM（支援向量機，Support Vector Machine）演算法作鋪墊。Andrew Ng在講解最優間隔分類器時運用了廣泛拉格朗日乘子法但並沒有講的十
最優化：拉格朗日乘子法
作者：桂。 時間：2017-03-27 20:26:17 宣告：歡迎被轉載，不過記得註明出處哦~ 【讀書筆記06】 前言 看到西蒙.赫金的《自適應濾波器原理》第四版第四章：最速下降演算法。最速下降法、擬牛頓法等都是求解準則函式（即無約束優化問題）的演算法，這就需要有一個前提：怎樣得
基礎數學知識（一）——拉格朗日乘子法
這幾天一直在看支援向量機，然後就是大量大量的數學公式，一直迷迷糊糊的，然後一直遇到拉格朗日，拉格朗日，原來數學基礎也不好，沒怎麼學過，於是下定決心要把拉格朗日乘子法搞懂，花了幾天，看了一些文章，算是對拉格朗日乘子法有了簡單的瞭解，下面就和大家簡單的分享分享啦