計算幾何問題彙總--圓與矩形

阿新 • • 發佈：2019-02-03

我在上一篇部落格中（詳見：計算幾何問題彙總–點與線的位置關係）談到了計算幾何最基本的問題：解決點與線（線段or直線）的位置關係判斷。那麼，更進一步，還需要探討複雜一點的情況：比如面與線，面與面之間的關係。本文中，我就先說說最常見的兩種幾何圖形：圓與矩形。我將就矩形與圓的碰撞判斷問題、線與矩形、線與圓之間的碰撞問題作出分析，以及給出這些解決問題的演算法、程式碼。

在此之前，我預設所有對本文內容感興趣的讀者，都瞭解基本的計算幾何概念，並且對我的上一篇部落格：計算幾何問題彙總–點與線的位置關係所講的內容基本熟悉。因為本文涉及的演算法，幾乎全部都用到了上一篇部落格中所定義的類和函式。

簡單將上一篇部落格的內容陳列如下，方便讀者閱讀後面本文的演算法：

模組名：PointLine

class Point: 點類，兩個屬性，分別是橫縱座標x, y

class Segment: 線段類，兩個屬性，分別是兩個端點p1, p2

class Line: 直線類，兩個屬性，分別是直線上任意兩點p1, p2

class Vector: 向量類，以向量的起點和終點為引數，建立一個由橫縱座標為兩個屬性的類

func: pointDistance(p1, p2): 計算兩點之間距離的函式。返回一個浮點型的值

func: pointToLine(C, AB): 計算點C到直線AB的距離。返回一個浮點型的值

func: pointInLine(C 
, AB): 判斷點C是否在直線AB上。在，返回True；不在，返回False

func: pointInSegment(C, AB): 判斷點C是否線上段AB上。在，返回True；不在，返回False

func: linesAreParallel(l1, l2): 判斷兩條直線l1, l2是否平行。平行，返回True；不平行，返回False

func: crossProduct(v1, v2): 計算兩個向量叉積

func: segmentsIntersect(s1, s2): 判斷兩個線段是否相交

func: segmentIntersectsLine(segment, line 
): 判斷一條線段和一條直線是否相交

好了，以上是我在上一篇部落格中定義的類和函式，我把他們的基本功能，引數設定等等簡要列在了上面，以便理解本文後面將要給出的程式碼。至於具體的演算法及分析，請翻看我的上一篇部落格。

需要注意的是，我在本文中，把上一篇部落格的工作全部封裝成了一個模組：PointLine.py，方便本文的程式碼呼叫。

接下來，就進入本文的主題吧。

圓

1. 圓與點的位置關係

簡單來分，二維空間內，圓與點的位置關係，只有兩種：

(1)點在圓上（包括在圓周上以及在圓內）；
(2)點在圓外

而判斷的方法很直接，計算點到圓心的距離，再用這個距離和圓的半徑比較即可。

先定義一個圓類：兩個屬性，圓心及半徑。

class Circle(object):
    """Circle has 2 attributes: center and radius"""

    def __init__(self, center, radius):
        self.center = center
        self.radius = radius

然後寫出判斷點與圓關係的完整程式碼如下：

from PointLine import *


class Circle(object):
    """Circle has 2 attributes: center and radius"""

    def __init__(self, center, radius):
        self.center = center
        self.radius = radius


def pointInCircle(point, circle):
    """determine whether a point in a circle"""

    return (pointDistance(point, circle.center) - circle.radius) < 1e-9

其中，pointDistance() 函式在模組 PointLine 已經存在。

最後的距離判斷還是要滿足浮點值比較的原則，上一篇部落格中詳細說過，不再贅述。

2. 圓與線的位置關係

(1) 圓與直線的位置關係

簡單劃分，還是兩種：相交（包括相切）；不相交

判斷的依據是根據圓心到直線的距離與圓半徑相比較。判別函式如下：

def lineIntersectsCircle(line, circle):
    """determine whether a line intersects a circle"""

    dis = pointToLine(circle.center, line)
    return dis - circle.radius < 1e-9

其中，pointToLine() 在模組PointLine中已經存在。

(2) 圓與線段的位置關係

線段由於其位置上的限制，導致我們在判斷線段和圓的關係的時候會麻煩一點。判斷思路如下：

判斷線段s所在的直線l與圓心的距離dis和圓的半徑r之間的關係。若dis<=r 則進行2、3步的判斷；若dis>r ，直接返回False.（也就是說肯定與圓不相交）
計算出圓心到直線l的垂線與直線l的交點（也就是垂足），記為點D. 此處的計算方法參考我在上一篇部落格中計算點到直線距離時，所使用的向量法。（詳見：計算幾何問題彙總–點與線的位置關係）
判斷點D是否線上段s上，判斷方法是 PointLine 模組中的函式PointInSegment()。這裡直接呼叫就行。

程式碼如下：

def segmentIntersectsCircle(AB, circle):
    """determine whether a segment intersects a circle"""

    if not lineIntersectsCircle(Line(AB.p1, AB.p2), circle):
        return False

    if pointInCircle(AB.p1, circle) or pointInCircle(AB.p2, circle):
        return True

    vector_AB = Vector(AB.p1, AB.p2)
    vector_AO = Vector(AB.p1, circle.center)

    # two ndarray object
    tAB = np.array([vector_AB.x, vector_AB.y])
    tAO = np.array([vector_AO.x, vector_AO.y])

    # vector AD, type: ndarray
    tAD = ((tAB @ tAO) / (tAB @ tAB)) * tAB

    # get point D
    Dx, Dy = tAD[0] + AB.p1.x, tAD[1] + AB.p1.y
    D = Point(Dx, Dy)

    return pointInCircle(D, circle) and pointInSegment(D, AB)

執行此函式的前提是還是匯入模組PointLine以及庫numpy

把上面的所有函式寫在一起，方便有需要的讀者使用：

from PointLine import *


class Circle(object):
    """Circle has 2 attributes: center and radius"""

    def __init__(self, center, radius):
        self.center = center
        self.radius = radius


def pointInCircle(point, circle):
    """determine whether a point in a circle"""

    return (pointDistance(point, circle.center) - circle.radius) < 1e-9


def lineIntersectsCircle(line, circle):
    """determine whether a line intersects a circle"""

    dis = pointToLine(circle.center, line)
    return dis - circle.radius < 1e-9


def segmentIntersectsCircle(AB, circle):
    """determine whether a segment intersects a circle"""

    if not lineIntersectsCircle(Line(AB.p1, AB.p2), circle):
        return False

    if pointInCircle(AB.p1, circle) or pointInCircle(AB.p2, circle):
        return True

    vector_AB = Vector(AB.p1, AB.p2)
    vector_AO = Vector(AB.p1, circle.center)

    # two ndarray object
    tAB = np.array([vector_AB.x, vector_AB.y])
    tAO = np.array([vector_AO.x, vector_AO.y])

    # vector AD, type: ndarray
    tAD = ((tAB @ tAO) / (tAB @ tAB)) * tAB

    # get point D
    Dx, Dy = tAD[0] + AB.p1.x, tAD[1] + AB.p1.y
    D = Point(Dx, Dy)

    return pointInCircle(D, circle) and pointInSegment(D, AB)

這就可以構成一個關於圓的相關問題的計算模組了。其中，引入的模組 PointLine 詳見我的上一篇部落格，連結前面已經給出了。

矩形

瞭解了圓的問題之後，我們看看矩形。這裡，我將圓與矩形的位置關係，也放在矩形中講解。

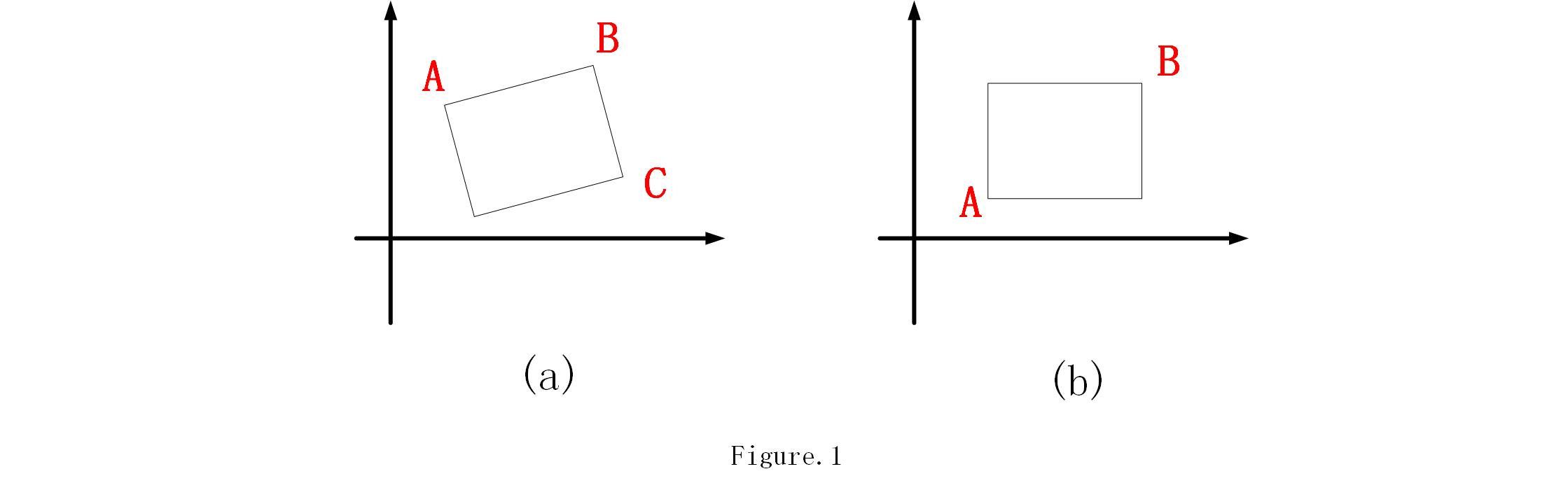
在二維平面空間中，若要定義矩形，則至少需要知道矩形的三個頂點，如Fig.1(a)所示。若是有矩形的邊一定和座標軸平行或垂直的條件，則只需要知道兩個頂點就行，如Fig.1(b)所示。為使演算法具有普遍性，我們研究Fig.1(a)所示的情況：

這裡寫圖片描述

先給出矩形類：

class Rectangle(object):
    """four points are defined by clockwise order from upper left corner"""

    def __init__(self, p1, p2, p3, p4):
        self.p1, self.p2, self.p3, self.p4 = p1, p2, p3, p4

    def getCenter(self):

        return Point((self.p2.x + self.p4.x) / 2, (self.p2.y + self.p4.y) / 2)

    def getXline(self):

        rectangle_center = self.getCenter()
        x_center = Point((self.p2.x + self.p3.x) / 2, (self.p2.y + self.p3.y) / 2)
        return Line(x_center, rectangle_center)

    def getYline(self):

        rectangle_center = self.getCenter()
        y_center = Point((self.p1.x + self.p2.x) / 2, (self.p1.y + self.p2.y) / 2)
        return Line(y_center, rectangle_center)

建構函式中，用矩形的四個頂點構造了一個矩形物件，其實，三個頂點就夠了，但在這裡，4個還是3個影響不大。

此外，除了初始化物件的建構函式，我還給出了三個矩形類的方法：

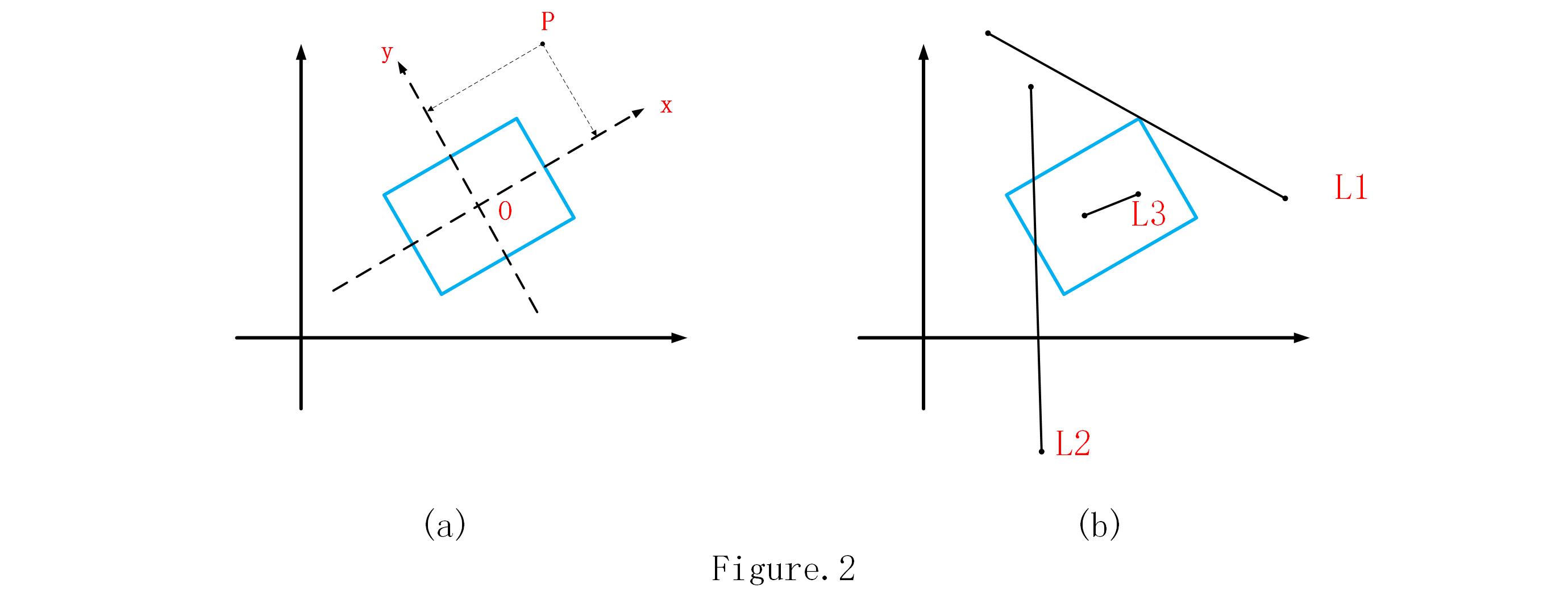
getCenter：用來返回矩形的中心點，也就是Fig.2(a)中的點O；
getXline：用來返回經過矩形的中心點O，且平行於矩形一邊的軸線，作為針對某個矩形的新的X軸。如Fig.2(a)所示；
getYline：與矩形新的X軸的構造同理，構造一個針對某個矩形的Y軸

顯而易見，如果對一個矩形物件執行以上三種方法，我們就可以得到一個以矩形中心點為座標原點，分別平行於矩形的高和寬的新的座標系。

1. 點和矩形的位置關係

明確了這一點，再看問題。首先解決點是否在矩形中的問題（這裡說的在矩形中，包括在矩形邊線上的情況）：

這裡寫圖片描述

想要一個點，比如Fig.2(a)中的點P，在矩形中，那麼這個點與上面所說的新建的座標系一定要同時滿足以下兩個條件：

點P到新的X軸的距離小於等於矩形高度的1/2
點P到新的Y軸的距離小於等於矩形寬度的1/2

由此，可以寫出程式碼：

from PointLine import *


def pointInRectangle(point, rectangle):
    """determine whether a point in a rectangle"""

    x_line = rectangle.getXline()
    y_line = rectangle.getYline()
    d1 = pointToLine(point, y_line) - pointToLine(rectangle.p2, y_line)
    d2 = pointToLine(point, x_line) - pointToLine(rectangle.p2, x_line)

    return d1 < 1e-9 and d2 < 1e-9

函式 PointToLine() 在模組PointLine中給出了。

2. 線和矩形的位置關係

藉助點和矩形位置關係的判斷方法，我們可以判斷線段和矩形的位置關係。若一條線段和矩形相交（包括線段和矩形的邊相交以及線段在矩形內的情況），那麼線段必須滿足以下兩個條件之一：

線段的兩個端點全部在矩形內
線段和至少一條矩形的邊相交

如圖Fig.2(b)所示，線段和矩形相交的情況都可以被以上的兩個條件涵蓋。因此，根據這個思路寫出程式碼即可。

def segmentIntersectsRectangle(s, rectangle):
    """determine whether a segment intersects a rectangle"""

    s1 = Segment(rectangle.p1, rectangle.p2)
    s2 = Segment(rectangle.p2, rectangle.p3)
    s3 = Segment(rectangle.p3, rectangle.p4)
    s4 = Segment(rectangle.p4, rectangle.p1)

    segmentsList = [s1, s2, s3, s4]

    if pointInRectangle(s.p1, rectangle) and pointInRectangle(s.p2, rectangle):
        return True

    for segment in segmentsList:
        if segmentsIntersect(segment, s):
            return True
    return False

s1−s4是矩形的四條邊，都是線段。

同理，可以寫出直線與矩形位置關係的判別函式。與線段不同的是，直線與矩形任意邊相交
是直線與矩形相交的充要條件。給出程式碼，如下：

def lineIntersectsRectangle(l, rectangle):
    """determine whether a line intersects a rectangle"""

    s1 = Segment(rectangle.p1, rectangle.p2)
    s2 = Segment(rectangle.p2, rectangle.p3)
    s3 = Segment(rectangle.p3, rectangle.p4)
    s4 = Segment(rectangle.p4, rectangle.p1)

    segmentsList = [s1, s2, s3, s4]

    for segment in segmentsList:
        if segmentIntersectsLine(segment, l):
            return True
    return False

3. 圓與矩形的碰撞檢測

現在，已經解決了圓和矩形的基本計算問題，那麼如何確定圓跟矩形的位置關係呢，換句話說，如何設計一個檢測圓與矩形是否碰撞的演算法？

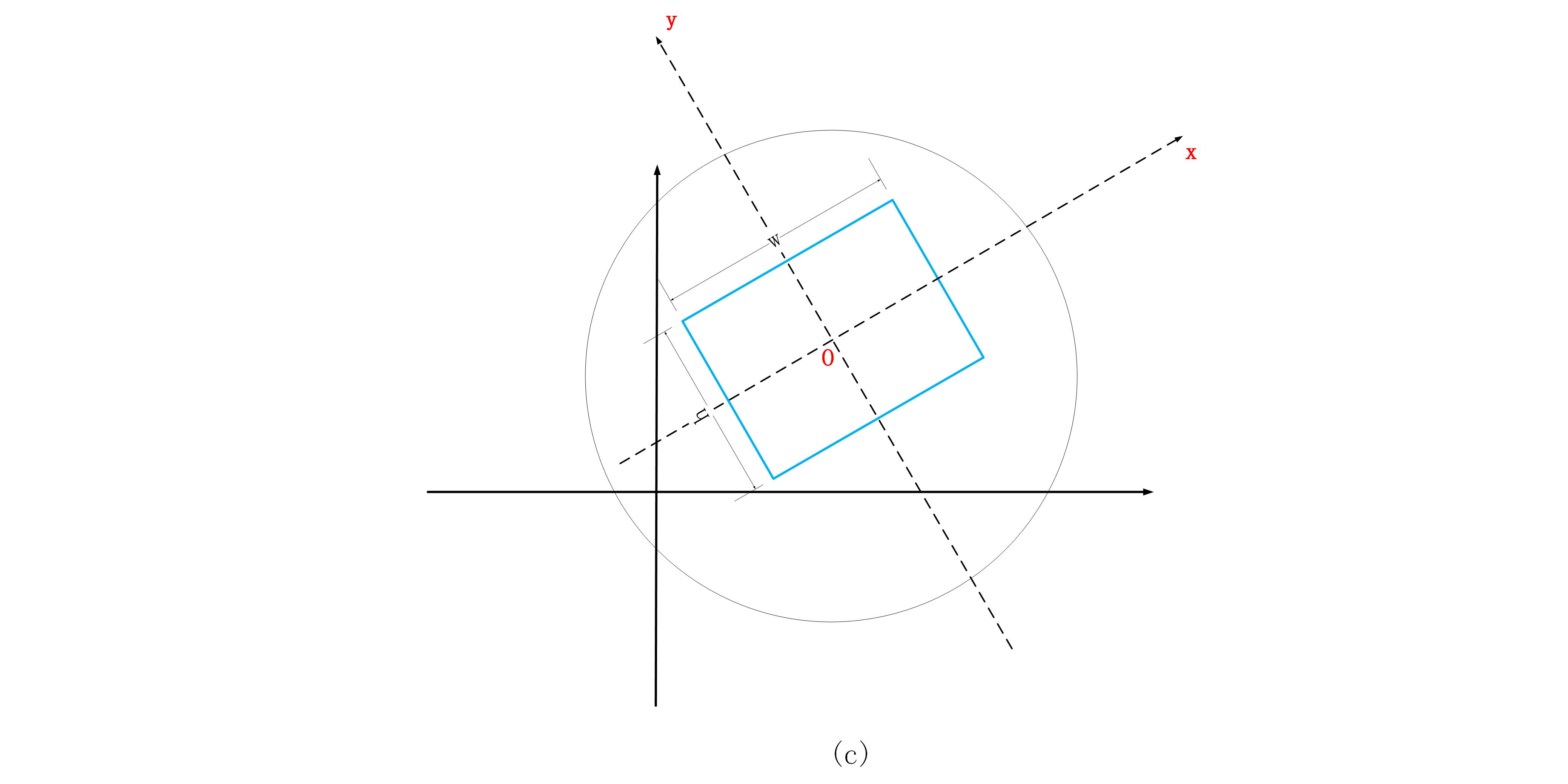
和判斷線與矩形，點與矩形的辦法一樣，還是需要先根據矩形，建立新的座標系，如圖Fig.3所示，然後計算圓心到這個新座標系X軸和Y軸的距離，根據這個距離與圓的半徑、矩形邊長的關係可以檢測碰撞。

先想一想圓和矩形碰撞的碰撞（相交）的情況，其實一共就三種：

圓只與矩形的一條邊相交，並不和矩形的頂點相交。如圖Fig.3(a)所示
圓與矩形的一個或多個頂點相交，也包含了矩形完全在圓內的情況。如圖Fig.3(b)所示
圓在矩形內。如圖Fig.3(c)所示

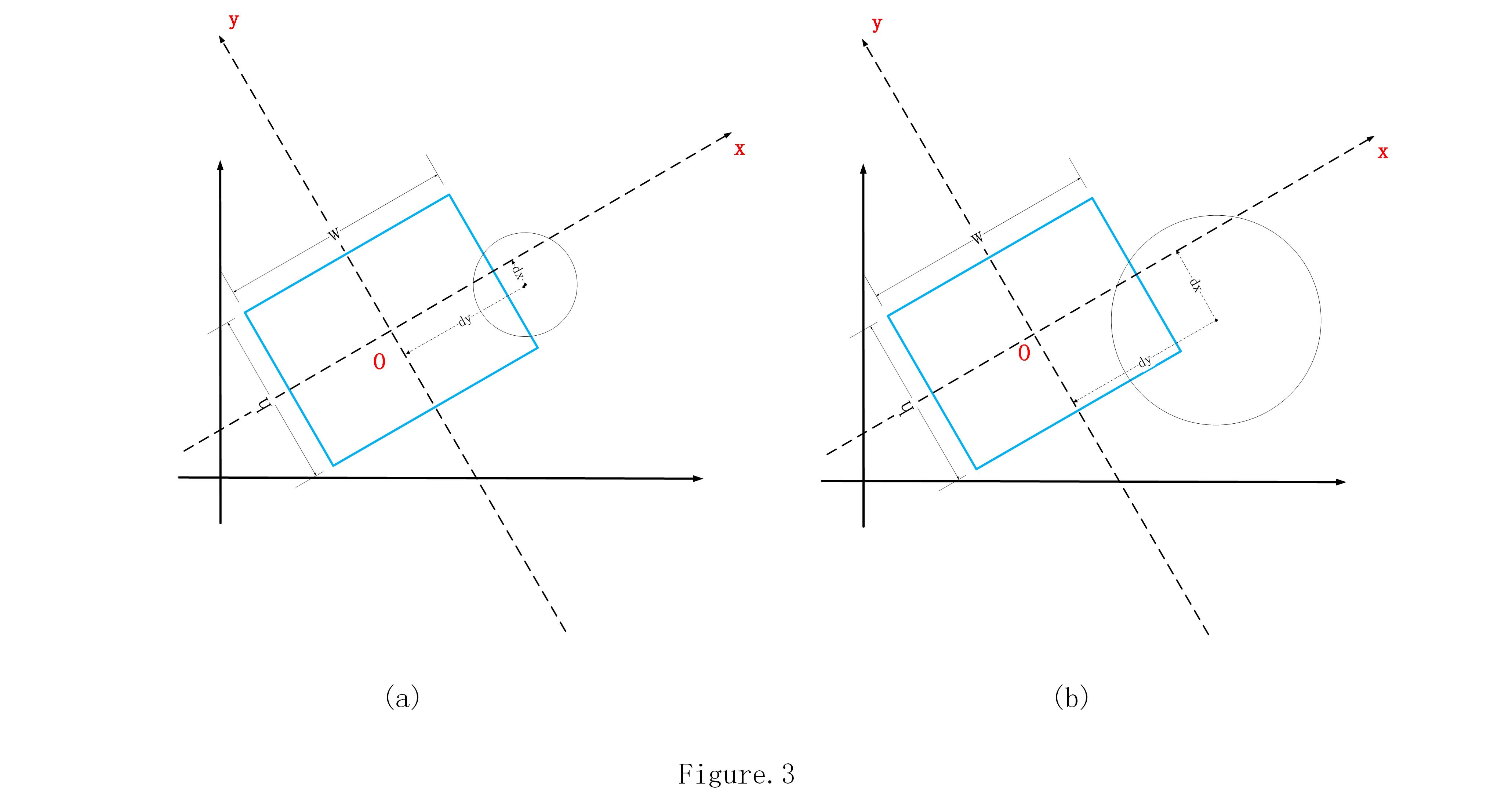
這裡寫圖片描述

現在，設dx為圓心到新座標系X軸的距離，而dy為圓心到新座標系Y軸的距離，w為矩形的寬度，h為矩形的高度。就像Fig.3中所標出的那樣。

可以按如下思路討論：

判斷矩形的四個頂點是否在圓中，只要有一個在，那麼矩形與圓碰撞。也就是上面說的情況2；
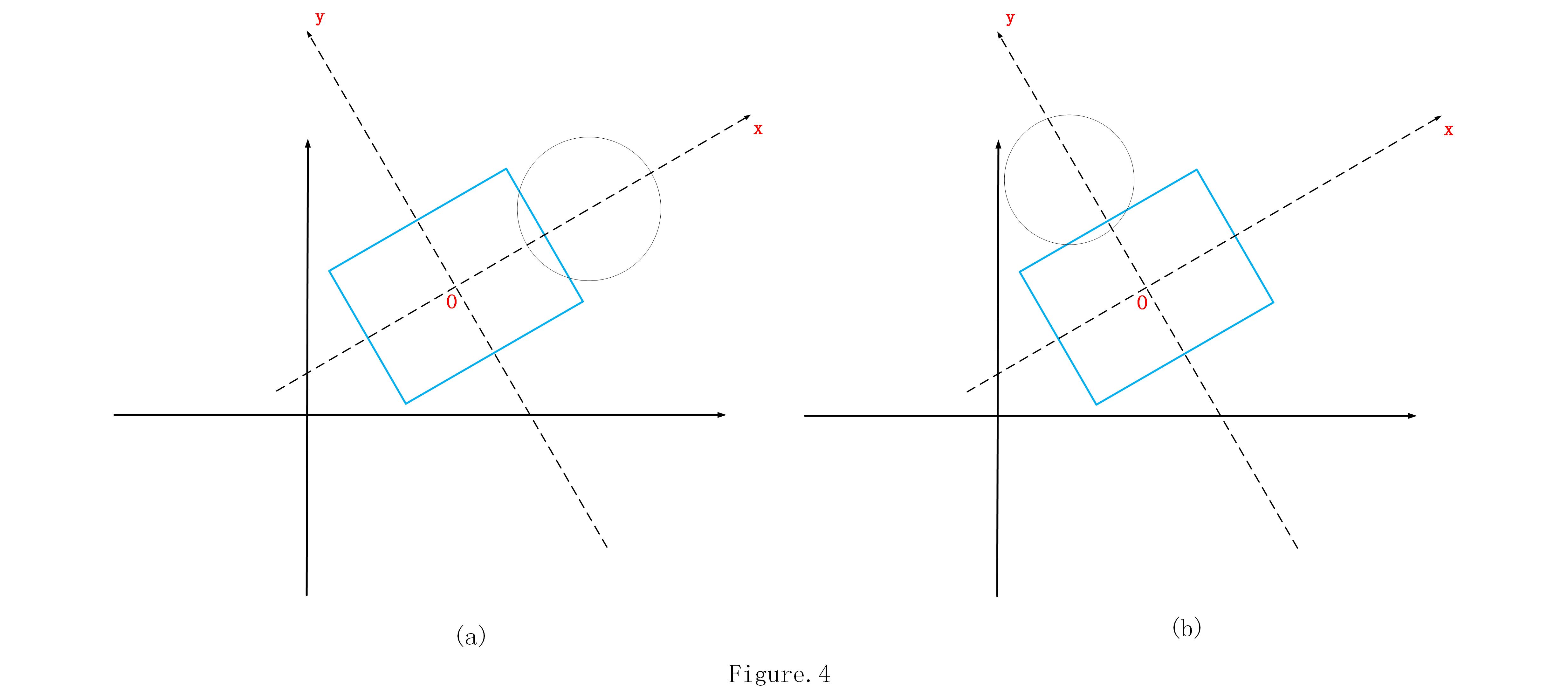
判斷dx<=h2 且 dy<=r+w2是否成立，若成立，則圓一定與矩形的一條高相交，如圖Fig.4(a)所示；
判斷dy<=w2 且 dy<=r+h2是否成立，若成立，則圓一定與矩形的一條寬相交，如圖Fig.4(b)所示；
最後需要說明的是，對於圓在矩形內的情況，2、3步就可以判斷了，無需再寫程式碼；

這裡寫圖片描述

程式碼如下：

def circleIntersectsRectangle(circle, rectangle):
    """determine whether a circle intersects a rectangle"""

    if pointInCircle(rectangle.p1, circle) or pointInCircle(rectangle.p1, circle) or\
            pointInCircle(rectangle.p1, circle) or pointInCircle(rectangle.p1, circle):
        return True

    x_line = rectangle.getXline()
    y_line = rectangle.getYline()

    dx, dy = pointToLine(circle.center, x_line), pointToLine(circle.center, y_line)
    h, w = pointDistance(rectangle.p1, rectangle.p2), pointDistance(rectangle.p2, rectangle.p3)

    if dx - h / 2 < 1e-9 and dy - (circle.radius + w / 2) < 1e-9:
        return True

    if dy - w / 2 < 1e-9 and dx - (circle.radius + h / 2) < 1e-9:
        return True

    return False

關於矩形的相關計算的完整程式碼我放在這裡，方便參考：


from Circle import *
from PointLine import *


class Rectangle(object):
    """four points are defined by clockwise order from upper left corner"""

    def __init__(self, p1, p2, p3, p4):
        self.p1, self.p2, self.p3, self.p4 = p1, p2, p3, p4

    def getCenter(self):

        return Point((self.p2.x + self.p4.x) / 2, (self.p2.y + self.p4.y) / 2)

    def getXline(self):

        rectangle_center = self.getCenter()
        x_center = Point((self.p2.x + self.p3.x) / 2, (self.p2.y + self.p3.y) / 2)
        return Line(x_center, rectangle_center)

    def getYline(self):

        rectangle_center = self.getCenter()
        y_center = Point((self.p1.x + self.p2.x) / 2, (self.p1.y + self.p2.y) / 2)
        return Line(y_center, rectangle_center)


def pointInRectangle(point, rectangle):
    """determine whether a point in a rectangle"""

    x_line = rectangle.getXline()
    y_line = rectangle.getYline()
    d1 = pointToLine(point, y_line) - pointToLine(rectangle.p2, y_line)
    d2 = pointToLine(point, x_line) - pointToLine(rectangle.p2, x_line)

    return d1 < 1e-9 and d2 < 1e-9


def segmentIntersectsRectangle(s, rectangle):
    """determine whether a segment intersects a rectangle"""

    s1 = Segment(rectangle.p1, rectangle.p2)
    s2 = Segment(rectangle.p2, rectangle.p3)
    s3 = Segment(rectangle.p3, rectangle.p4)
    s4 = Segment(rectangle.p4, rectangle.p1)

    segmentsList = [s1, s2, s3, s4]

    if pointInRectangle(s.p1, rectangle) and pointInRectangle(s.p2, rectangle):
        return True

    for segment in segmentsList:
        if segmentsIntersect(segment, s):
            return True
    return False


def lineIntersectsRectangle(l, rectangle):
    """determine whether a line intersects a rectangle"""

    s1 = Segment(rectangle.p1, rectangle.p2)
    s2 = Segment(rectangle.p2, rectangle.p3)
    s3 = Segment(rectangle.p3, rectangle.p4)
    s4 = Segment(rectangle.p4, rectangle.p1)

    segmentsList = [s1, s2, s3, s4]

    for segment in segmentsList:
        if segmentIntersectsLine(segment, l):
            return True
    return False


def circleIntersectsRectangle(circle, rectangle):
    """determine whether a circle intersects a rectangle"""

    if pointInCircle(rectangle.p1, circle) or pointInCircle(rectangle.p1, circle) or\
            pointInCircle(rectangle.p1, circle) or pointInCircle(rectangle.p1, circle):
        return True

    x_line = rectangle.getXline()
    y_line = rectangle.getYline()

    dx, dy = pointToLine(circle.center, x_line), pointToLine(circle.center, y_line)
    h, w = pointDistance(rectangle.p1, rectangle.p2), pointDistance(rectangle.p2, rectangle.p3)

    if dx - h / 2 < 1e-9 and dy - (circle.radius + w / 2) < 1e-9:
        return True

    if dy - w / 2 < 1e-9 and dx - (circle.radius + h / 2) < 1e-9:
        return True

    return False

有關於計算幾何問題的完整專案我放在了github主頁上，並持續更新：Computational-Geometry. 歡迎訪問。

計算幾何問題彙總--圓與矩形

圓

1. 圓與點的位置關係

2. 圓與線的位置關係

矩形

1. 點和矩形的位置關係

2. 線和矩形的位置關係

3. 圓與矩形的碰撞檢測

計算幾何問題彙總--圓與矩形

計算幾何：直線與圓的交點三角形的內切圓和外接圓(5252: Triangle to Hexagon)

1015 - 計算幾何之點與多邊形的關係 - Points Within（ZOJ1081）

1015 - 計算幾何之直線與直線的關係 - Intersecting Lines（POJ1269）

1016 - 計算幾何之點與直線的關係 - TOYS（POJ 2318）

1016 - 計算幾何之直線與線段的交 - Segments（POJ 3304）

UVa12304（計算幾何中圓的基本操作）

計算機與數學 —— 檢測圓與矩形相交的快速判定演算法

OpenCV-圓與矩形識別

hdu5858Hard problem+計算幾何（圓的面積交）

51 Nod 1298 圓與三角形（計算幾何）

[計算幾何] 圓與圓的交點座標

[計算幾何] (二維)圓與直線的交點

51Nod 1298 圓與三角形（計算幾何）

計算幾何問題彙總--點與線的位置關係

【bzoj1043】[HAOI2008]下落的圓盤計算幾何

【計算幾何】【圓反演】hdu6158 The Designer

HDU 6206 Apple ( 高精度 && 計算幾何 && 三點構圓求圓心半徑 )

JZYZOJ1502 [haoi2008]下落的圓盤計算幾何貪心

bzoj1043[HAOI2008]下落的圓盤計算幾何

計算幾何問題彙總--圓與矩形

圓

1. 圓與點的位置關係

2. 圓與線的位置關係

矩形

1. 點和矩形的位置關係

2. 線和矩形的位置關係

3. 圓與矩形的碰撞檢測

相關推薦