編輯距離

編輯距離（Edit Distance），又稱Levenshtein距離，是指兩個字串之間，由一個轉成另一個所需的最少編輯操作次數。許可的編輯操作包括將一個字元替換成另一個字元，插入一個字元，刪除一個字元。一般來說，編輯距離越小，兩個串的相似度越大。度娘

動態規劃解法

記 S1 的字串長 n1，S2的字串長 n2，用 S(i) 來表示字串中的 i 個字元。dis[n1,n2] 表示 S1 的前 i個字串的子串與 S2 的前 j 個字元構成的子串之間的編輯距離。

對於S1 、S2 有一個是空串，另一個的 dis[i,0]=i 或者 dis[0，j]=j

演算法步驟：

（哎。。。CSDN 的Markdown 真是無力吐槽。。。）

來來來 上程式碼 申請的空間記得釋放

#include <iostream>
using namespace std;

int editableDistance(string strFrom,string
 
 strDest);
void initialArray2D(int** arrayTemp,int m,int n);
void free2DArray(int** arrayTemp,int m,int n);
void displayArray2D(int** arrayTemp,int m,int n);
int minNumber(int num1,int num2,int num3);

int main()
{
    string strOne="I LOVE READING";
    string strTwo="I LOVE EATING";
    cout<<"Please Enter Two Strings:\n"
 
;
    //cin>>strOne>>strTwo;
    int result = editableDistance(strOne,strTwo);
    cout<<"\nThe distance between "<<strOne<<" and "<<strTwo<<"is "<<result<<endl;

    return 0;
}

int editableDistance(string strFrom,string strDest){
    int lenFrom = strFrom.length();
    int lenDest = strDest.length();
    int distace = 0;
    //宣告並初始化二維陣列
    int** arrayDis = new int*[lenFrom+1];//2D array
    for(int i=0;i<=lenFrom;++i){
        arrayDis[i]= new int[lenDest+1];
    }
    initialArray2D(arrayDis,lenFrom,lenDest);

    //初始化距離陣列
    for(int j=1;j<=lenDest;++j){   //dis[0,j]<-j
        arrayDis[0][j]=j;
    }
    for(int i=1; i<=lenFrom; ++i)
    {
        arrayDis[i][0]=i;//dis[i,0]<-i
        for(int j=1; j<=lenDest; ++j)
        {
            if(strFrom[i-1]==strDest[j-1]){
                arrayDis[i][j]=arrayDis[i-1][j-1];
            }else{
                arrayDis[i][j]=minNumber(arrayDis[i-1][j],arrayDis[i-1][j-1],arrayDis[i][j-1])+1;
            }
        }
    }
    //輸出距離矩陣
    displayArray2D(arrayDis,lenFrom,lenDest);
    distace = arrayDis[lenFrom-1][lenDest-1];
    free2DArray(arrayDis,lenFrom,lenDest);
    return distace;
}
//初始化二維陣列
void initialArray2D(int** arrayTemp,int m,int n){
    for(int i=0;i<=m;++i){
        for(int j=0;j<=n;++j){
            arrayTemp[i][j]=0;
            //cout<<arrayTemp[i][j];
        }
    }
}
//動態陣列的刪除操作
void free2DArray(int** arrayTemp,int m,int n){
    for(int i=m;i>=0;--i){
        delete[] arrayTemp[i];
        arrayTemp[i] = NULL;
    }
    arrayTemp=NULL;
}
//輸出二維陣列
void displayArray2D(int** arrayTemp,int m,int n){
     for(int i=0;i<=m;++i){
            cout<<endl;
        for(int j=0;j<=n;++j){
            cout<<arrayTemp[i][j]<<"\t";
        }
    }
}
//求三個數的最大值
int minNumber(int num1,int num2,int num3){
    return min(min(num1,num2),num3);
}

此外，對於每次進行第 i 行的判斷。。。其前面 i−1 行的資訊已經沒有用了，因此可以將動態二維陣列減少為兩個陣列，分別來標記當前行和前一行的值。

廢話不說上程式碼。。。

#include <iostream>

using namespace std;

int editableDistance(string strFrom,string strDest);
int minNumber(int num1,int num2,int num3);

int main()
{

    string strOne="TJU";
    string strTwo="NKU";
    cout<<"Please Enter Two Strings:\n";
    //cin>>strOne>>strTwo;
    int result = editableDistance(strOne,strTwo);
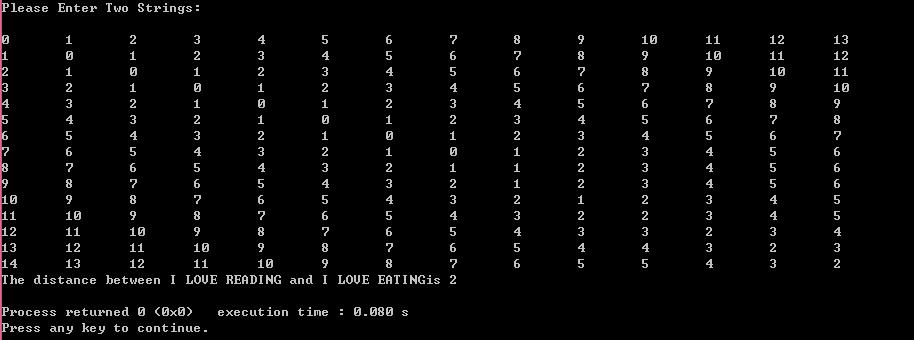
    cout<<"\nThe distance between "<<strOne<<" and "<<strTwo<<"is "<<result<<endl;

    return 0;
}

int editableDistance(string strFrom,string strDest){
    int lenFrom = strFrom.length();
    int lenDest = strDest.length();
    int arrayLen = max(lenFrom,lenDest);
    int distance = 0;//記錄距離
    //宣告並初始化二維陣列
    int* arrayOld = new int[arrayLen+1];
    int* arrayNew = new int[arrayLen+1];
    int* tempPointer = NULL;
    //初始化距離陣列
    for(int j=0;j<=lenDest;++j){   //d[0,j]<-j
        arrayOld[j]=j;
    }
    for(int i=1; i<=lenFrom; ++i)
    {
        arrayNew[0]=i;//d[i,0]<-i
        for(int j=1; j<=lenDest; ++j)
        {
            if(strFrom[i-1]==strDest[j-1]){
                arrayNew[j]=arrayOld[j-1];
            }else{
                arrayNew[j]=minNumber(arrayNew[j-1],arrayOld[j-1],arrayOld[j])+1;
            }
        }
        //交換
        tempPointer=arrayOld;
        arrayOld = arrayNew;
        arrayNew = tempPointer;
    }
    distance = arrayOld[arrayLen];
    delete[] arrayNew;arrayNew=NULL;
    delete[] arrayOld;arrayOld=NULL;
    tempPointer = NULL;
    return distance;//因為與arrayNew交換了，所以old是最新的結果
}

//求三個數的最大值
int minNumber(int num1,int num2,int num3){
    return min(min(num1,num2),num3);
}

哎。。。友情贈送演算法虛擬碼的 LATEX原始碼。。。不要太感動。。。吼吼吼

\documentclass[11pt]{article}
\usepackage{CJK}
\usepackage[top=2cm, bottom=2cm, left=2cm, right=2cm]{geometry}
\usepackage{algorithm}
\usepackage{algorithmicx}
\usepackage{algpseudocode}
\usepackage{amsmath}
\begin{CJK*}{UTF8}{gkai}
    \begin{algorithm}
        \caption{編輯距離的動態規劃演算法}
        \begin{algorithmic}[1] %每行顯示行號   
        \For{$j \in \{1,2,...,n_2\}$} \do\\
        \State  $dis[0,j] \gets j$
        \EndFor
        \For{$i \in \{1,2,...,n_1\}$} \do\\
        \State  $dis[i,0] \gets i$
             \For{$j \in \{1,2,...,n_2\}$} \do\\
                \If{$S_1(i) == S_2(j) then$ } 
                \State $dis[i,j] \gets dis[i-1,j-1]$
                \Else
                \State $dis[i,j] \gets min \{dis[i,j-1],dis[i-1,j],dis[i-1,j-1]\}+1$
                \EndIf
             \EndFor
        \EndFor             

        \end{algorithmic}
    \end{algorithm}
\end{CJK*}
\end{document}

閱讀書目

1. 刁瑞, 謝妍. 演算法筆記[M]. 電子工業出版社, 2016.