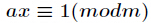2. 程式人生 > >NOIP數學複習

NOIP數學複習

阿新 • • 發佈：2019-02-08

NOIP中的數學相關知識

素數及其相關

a.判斷素數 複雜度O(根號n)

bool prime(int x) {
    if(x == 0 || x == 1) return false;
    for(int i = 2; i * i <= x; i++) {
        if(x % i == 0) return false;
    }
    return true;

b.篩素數

埃氏篩法 複雜度O(n loglog n)

對於每個數p，會劃掉p/n個數

#include<iostream>
#include<cstdio>
 

using namespace std;
const int SIZE=1e7;

int prime[SIZE];// 第i個素數
bool is_prime[SIZE];//true表示i是素數

int slove(int n)
{
    int p = 0;
    for(int i = 0; i <= n; i++)
        is_prime[i] = true;//初始化
    is_prime[0] = is_prime[1] = false;//0,1不是素數
    for(int i = 2; i <= n; i++)
    {
        if(is_prime[i])//zkzk
 

        {
            prime[p++] = i;//計算素數的個數,也記錄下了素數
            for(int j = 2 * i; j <= n; j += i)// 除掉了i的倍數的數字
                is_prime[j] = false;
        }
    }
    return p;
}

int main()
{
    int n;
    while(cin >> n)
    {
        int res = slove(n);
        cout << res << endl;//素數個數 
 

        for(int i = 0; i < res; i++)//列出素數 
            cout << prime[i] << endl;
    }
}
//zk:初始最小素數是2，將資料內2的所有倍數扔掉。此時3不能被更小的數整出，即為素數依次類推；

尤拉篩法 複雜度O（n）

luogu 線篩模板：

#include <cstdio>
using namespace std;
const int maxn=10000000;
int n,m;
int prime[maxn],flag[maxn];
int tot;
void get_prime(int n){
    flag[0]=flag[1]=1;//不是素數 
    for (int i=2; i<=n; ++i)
    {
        if (!flag[i]) prime[++tot]=i;
        for (int j=1; j<=tot&&i*prime[j]<=n; ++j)
        {
            flag[i*prime[j]]=1;
            if (i%prime[j]==0) break;//prime[j]必定是prime[j]*i的最小因子；i中有因子prime[j]，已被篩到一次 就退出找下一個i 
        }
    }
}
int main(){
    scanf("%d%d", &n, &m);
    get_prime(n);
    int t;
    for (int i=1; i<=m; ++i)
    {
        scanf("%d", &t);
        if (!flag[t]) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

2.區間篩素數

（poj2689）
篩[a，b）中的素數
因為b以內合數的最小質因數一定不超過sqrt(b),先分別做好[2,sqrt(b))的表和[a,b)的表，然後從[2,sqrt(b))的表中篩得素數的同時，也將其倍數從[a,b)的表中劃去，最後剩下的就是區間[a,b)內的素數。
用埃氏篩的原理：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const ll maxn=1e6+10;
bool is_prime[maxn],is_p[maxn];//is_prime[]表示le~ri中下邊位移後的素數判定（a位移1）,is_p[]表示1~根號n中的素數判定 
ll prime[maxn],sum;
void get_prime(ll le,ll ri){
    for(ll i=2;i*i<ri;i++) is_p[i]=true;//對[2,sqrt(b))的初始化全為質數,i要從2開始， 1不是素數 
    for(ll i=1;i<=ri-le;i++)    is_prime[i]=true;//對下標偏移後的[a,b)進行初始化，i要從1開始 
    for(ll i=2;i*i<=ri;i++){
        if(is_p[i])for(ll j=2*i;j*j<=ri;j+=i) is_p[j]=false;//篩選素數i的倍數 
        for(ll j=max(2LL,(le+i-1)/i) * i;j<=ri;j+=i) is_prime[j-le]=false;//(a+i-1)/i得到最接近a的i的倍數，最低是i的2倍，然後篩選
    }
    for(ll i=1;i<ri-le;i++) if(is_prime[i]) prime[++sum]=i+le;
}
int main(){
    ll l,r;
    while(scanf("%lld%lld",&l,&r)){
        sum=0;  memset(prime,0,sizeof(prime));
        get_prime(l,r);
        printf("%lld\n",sum);
    }
    return 0;
}

3.分解質因數

基於唯一分解定理
n = P1^a1 * P2^a2 * …………* Pn^an(P1 < P2 < ……Pn)，Pi為質數;
樸素法（可以先求出素數來優化一下）

void fj(int x) {
    for(int i = 2; i * i <= x && x > 1; i++) {
        while(x % i == 0) {
            if(!check[i]) zhi[++cnt] = i;//check判斷有沒有出現過
            check[i]++;
            x /= i;
            if(x == 1) break;
        }
    }
}

快速冪

// a ^ b % mod
int ksm(int a,int b,int mod) {
    int ans=1;
    a%=mod
    while(b){
        if(b&1)ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod
    }
    return ans;
}

排列組合

這裡寫圖片描述
這裡寫圖片描述

組合

void init(){
    f[0][0]=1;
    for(int i = 1; i <= inf; ++i){
        f[i][0]=1;
        for(int j = 1;j <= i; ++j){
            f[i][j] = f[i-1][j] + f[i-1][j-1];
        }
    }
}
next_permutation(a +１，ａ＋１＋ｎ)； STL全排列

同餘

同餘的性質

這裡寫圖片描述

0.0

這裡寫圖片描述
同餘方程

歐幾里得演算法

好久之前的筆記——關於gcd，exgcd，cal

/*設兩數為a、b(a>b)，求a和b最大公約數(a，b)的步驟如下:
用a除以b，得a÷b=q……r1(0≤r1)。
若r1=0，則(a，b)=b;若r1≠0，則再用b除以r1，得b÷r1=q……r2 (0≤r2).
若r2=0，則(a，b)=r1，若r2≠0，則繼續用r1除以r2，……
如此下去，直到能整除為止。其最後一個非零除數即為(a，b)。*/
//—————————————————————————————————-

#include<stdio.h>
#define ll long long 
ll gcd(ll a,ll b){
    return b==0?a:gcd(b,a%b);
}

int main(){
    ll a,b;
    while(scanf("%lld%lld",&a,&b)!=EOF)
    {
        printf("%lld\n",gcd(a,b));//事實上如果 a 小於 b，那第一次就會先交換 a 與 b。
    }
    return 0;
}
//--------------------------------------------------------
void exgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){d=a;x=1;y=0;}
    else {exgcd(b,a%b,d,y,x);y-=x*(a/b);}
}

//逆元

ll cal(ll a,ll m)
{
    ll d,x,y;
    exgcd(a,m,d,x,y);
    return (x%m+m)%m;
} 

int main(){
    ll a,b,d,x,y;
    while(scanf("%lld%lld",&a,&b)!=EOF){
        exgcd(a,b,d,x,y);
        printf("%lld*%lld+%lld*%lld=%lld\n",a,x,b,y,d);
    }
    return 0;
}

/*
同餘方程
先講一下擴充套件歐幾里德定律：

對於不完全為0的非負整數a，b，gcd(a, b)表示a, b的最大公約數，必定存在整數對x，y，滿足a*x+b*y==gcd(a, b)。

證明：（轉）

a*x1+b*y1=gcd(a, b);

b*x2+(a%b)*y2=gcd(b, a%b);

因為由歐幾里德定理知：gcd(a, b)==gcd(b, a%b)

所以a*x1+b*y1=b*x2+(a%b)*y2; 因為r=a%b, r =a-k*b所以==>

a*x1+b*y1=b*x2+(a-k*b)*y2; 因為k=a/b;所以==>

a*x1+b*y1=b*x2+(a-(a/b)*b)*y2; 展開得到==>

a*x1+b*y1=b*x2+a*y2-b*(a/b)*y2;轉換得到 ==>

a*x1+b*y1=a*y2+b*(x2-(a/b)*y2);

觀察上式可知 x1=y2, y1=x2-a/b*y2;

由此可知x1，y1是由x2，y2得出來的，由此類推x2，y2是由x3，y3得出來的，

那什麼時候是終止呢？也就是遞迴gcd(a, b)中b=0時；也就是說此時a的值就是要求得最大公約數

即gcd(a, 0)此時由擴充套件歐幾里得定律a*x+b*y==gcd(a, b)

知 a*x+b*y=a;

解出x=1, y=0;

此時就是遞迴終止的地方：

——————–分界線————————

那麼問題來了，這破東西有啥用呢

問的好，它可以用來求一個同餘方程的解，也就是逆元

ax ≡ 1 (mod b)，現在找x能夠使這個式子成立

這個式子等價於ax+by=1

這不就是拓展歐幾里得的表示式嗎，從這裡我們可以看出如果gcd(a,b)!=1那麼這個方程就不會有解

所以說呢

形如a*x + b*y = c這樣的式子，若c%gcd(a,b)==1，那麼這個方程就會有解

PS：題目保證有解，所以不用判斷了

但是一般題目裡會讓你求一個最小的x，當你用拓歐求出一個解時，一般會讓你去找一個最小解，我們只需要對這個數取模b就行了（如果求正數，你只需要先加一個b，再取模行了，應該都知道吧）

程式碼如下

#include <cstdio>
using namespace std;
typedef ll ll;
ll a,b,x,y;
ll e_gcd(ll a,ll b,ll &x,ll &y)
{
    if(!b)
    {
        x=1;
        y=0;
        return a;
    }
    ll ans=e_gcd(b,a%b,x,y);
    ll tmp=x;
    x=y;
    y=tmp-(a/b)*y;
    return ans;
} 
int main()
{
    scanf("%lld%lld",&a,&b);
    e_gcd(a,b,x,y);
    printf("%lld",(x+b)%b);
    return 0;
}

1.最大公因數

int gcd(int a,int b) {
    if(!b) return a;
    else return gcd(b, a % b);
}

2.最小公倍數

gcd(a,b) * lcm(a,b) = a * b; 
lcm（a，b） = a * b / gcd(a,b)；
int lcm(int a,int b) {
    return a * b / gcd(a,b);
}

霍dalao的醜字：
這裡寫圖片描述

擴充套件歐幾里得演算法

void exgcd(int a, int b, int &d, int &x, int &y) {
    if(!b) {d = a, x = 1, y = 0, return;}
    exgcd(b, a % b, d , y, x); 
    y -= x * (a / b);
}

擴歐求解不定方程：
這裡寫圖片描述

逆元

1.擴歐

這裡寫圖片描述

int inv(int a, int n) {
    int d,x,y;
    exgcd(a,n,d,x,y);
    return (x % n + n) % n;
}

2.費馬小定理

a^(p-1) ≡1 (mod p)

int inv(int a, int n) {
    return ksm(a,n-2,n)
}

遞推規律

1.Catalan數

這裡寫圖片描述

h(n)=(4n-2)/(n+1)*h(n-1)(n>1) h(0)=1 
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2) 
h(n)=C(2n,n)/(n+1)

2.錯排公式

十本不同的書放在書架上。現重新擺放，使每本書都不在原來放的位置。有幾種擺法？
f[1] = 0, f[2] = 1
f[i]=(i-1)*(f[n-1]+f[n-2])

3.斐波那契數列

f[1] = 1, f[2] = 1;
f[i] = f[i - 1] + f[i - 2]

5.除數函式

設 d(n)為 n 的所有因數的個數，由乘法原理可知，
d(n)＝(a1 +1)(a2 +1)…(ak +1)。

4.秦九韶演算法

這裡寫圖片描述

int qing(int x){
    int ans=a[n];
    for(int i=n-1;i>=1;i--)
        ans=ans*x+a[i];
    return ans;
}

相關推薦

NOIP數學複習

NOIP中的數學相關知識 素數及其相關 a.判斷素數 複雜度O(根號n) bool prime(int x) { if(x == 0 || x == 1) return false; for(int i = 2; i * i &

NOIp 數學知識點總結

cat 相交 per 一行 noi oid pan for play 推薦閱讀 NOIp 基礎數論知識點總結: https://www.cnblogs.com/greyqz/p/9473370.html 排列組合 常用公式 排列：\[\displaystyle A_n^

NOIP複賽複習（十五）動態規劃鞏固與提高

經典例題：數字金字塔（Luogu 1216）  寫一個程式來查詢從最高點到底部任意處結束的路徑，使路徑經過數字的和最大。每一步可以走到左下方的點也可以到達右下方的點。 我們現在這裡討論搜尋如何實現：  狀態：目前在第x行第y列 

NOIP複賽複習（十四）字串演算法鞏固與提高

一、Trie樹   1.定義： 通過字串建成一棵樹，這棵樹的節點個數一定是最少的。例如：4個字串"ab","abc","bd","dda"對應的trie樹如下： 其中紅色節點表示存在一個字串是以這個點結尾的。  一個性質：在樹上，兩個點u,

NOIP複賽複習（十三）圖論演算法鞏固與提高

一、圖的儲存   1、鄰接矩陣   假設有n個節點，建立一個n×n的矩陣，第i號節點能到達第j號節點就將[i][j]標記為1（有權值標記為權值），  樣例如下圖：   /*無向圖，無權值*/ i

NOIP複賽複習（十二）數論演算法鞏固與提高

一、數論    1.數   整數、自然數（大於等於0的整數）、正整數（大於0的整數）、負整數、非負整數、非正整數、非零整數、奇數偶數。   2.整除性   設a,b∈Z，如果存在c∈Z並且a=bc，則

NOIP複賽複習（十一）基礎演算法鞏固與提高

一、倍增演算法：   定義：用f[i][j]表示從i位置出發的2j個位置的資訊綜合（狀態） 一個小小的問題：為什麼是2j而不是3j,5j,…？因為，假設為kj，整個演算法的時間複雜度為(k-1)logk，當k=2時，時間複雜度最小。 這個演算法的三個應用：

NOIP複賽複習（十）怎樣才能拿到高分？

摘要 考場策略和程式測試是資訊學競賽中非常重要的環節，很多優秀的選手在很多比賽中總是會在這兩個環節上犯下這樣和那樣的錯誤，導致得到的分數和實力不成正比，最後留下了無盡的遺憾。本文將探討一些這兩個環節上值得注意的地方，提出一些可行的方法，分享一些經驗，以此希望幫助選手們在比賽中發揮水平，減少失

NOIP複賽複習（九）如何設計測試資料？

有些同學參加一次資訊學比賽之後，自我感覺非常不錯，但是測評結果成績卻並不理想。造成這種情況的原因有多方面，但是我認為其中不可忽視的一大原因就是在寫完程式之後，他們並不知道如何保證程式的正確性。在這裡，我就這個問題提出一點自己的看法。 先從考試的時間分配問題講起。很多同學覺得考試時間很充分，N

NOIP複賽複習（八）STL演算法與樹結構模板

STL演算法 STL 演算法是一些模板函式，提供了相當多的有用演算法和操作，從簡單如for_each（遍歷）到複雜如stable_sort（穩定排序），標頭檔案是：#include <algorithm>。常用STL 演算法庫包括：sort快速排序演算法、二分

NOIP複賽複習（七）STL容器與字串模板

STL容器 STL 容器是一些模板類，提供了多種組織資料的常用方法。常用的STL容器包括pair（組合）、list（列表，類似於連結串列）、vector（向量，類似於陣列）、priority_queue（優先佇列）、set（集合）、map（對映）、stack（棧）等，通過模板的引數

NOIP複賽複習（六）演算法分析與排序模板

演算法分析 演算法分析的目的是預測演算法所需的資源，如計算時間（CPU 消耗）、記憶體空間（RAM 消耗）、通訊時間（頻寬消耗）等，以及預測演算法的執行時間，即在給定輸入規模時，所執行的基本運算元量，或者稱為演算法複雜度。 演算法的執行時間取決於輸入的資料特徵，輸入

NOIP複賽複習（五）程式對拍與圖論模板

程式對拍 所謂“對拍”，顧名思義，就是讓兩者相互比對。所謂“兩者”，一是你要測試的程式，二是一個答案在該程式在一定範圍（時間/空間）內結果必定正確的程式（一般是用暴力求解的程式）。對拍一般需要造資料程式（data.exe），保證正確性的暴力對拍程式（test.exe）與測試程式（以moo.e

NOIP複賽複習（四）讀寫外掛與高精度模板

讀入輸出掛 讀入輸出掛就是逐個字元地讀入資料，從而讓讀入更加快速。輸出掛的原理也是一樣的，都是通過將輸出數字變成輸出字元以加快速度。當然輸入輸出外掛一般用在大量輸入輸出的情況下，這樣價效比才高一些，否則得不償失。 void Rd(int &res){  &nbs

NOIP複賽複習（三）檔案讀寫與數論模板

檔案讀入讀出 假設題目名為“add”，那麼資料夾名為“add”，c++程式名為“add.cpp”，讀入檔名為“add.in”，輸出檔名為“add.out”。四個的拼寫均不可有誤，包括大小寫差異。千萬不要除錯後就忘記修改檔案讀入讀出了。  #include<cstdio&

NOIP複賽複習（二）競賽環境與注意事項

一、比賽不提供紙質試題，只提供電子版試題檔案。 該檔案壓縮包儲存在計算機桌面上。監考人公佈密碼後，選手自行解密試題。 試題解壓密碼會影響一個人的心情，一定要一次輸對，注意大小寫，不要邊輸入邊檢查，要對自己有自信。 二、江蘇複賽選手上機可自選windows或linux作業系統。

NOIP複賽複習（一）常見問題與常用策略

數學類問題 1. 精度處理（高精度、實數處理、各種浮點型別處理方法） 2. 組合數學問題（斐波那契數列、第二類數、卡特蘭數、Polya原理、排列組合計數、加法原理與乘法原理） 3. 進位制問題（特定二進位制串的統計、二分查詢、利用二進位制進行路徑、狀

noip 數學整理

// 質數判定 (1) 暴力 bool check(int x) { for (int i = 2; i * i <= x; ++i) if (x % i == 0) return 0; return 1; } (2)miller_rabin bool check(L

NOIp數學

NOIp 數學基礎 目錄 素數判斷 gcd/exgcd 逆元 crt（中國剩餘定理） 線性代數 -快速冪 矩陣相關 高斯消元 組合數學 卡特蘭數 排列組合 Luca

離散數學複習--第二章：一階邏輯

2.1 一階邏輯基本概念 如果沒有事先給出一個個體域，都以全總個體域為個體域。於是，引入一個新的謂詞 M (