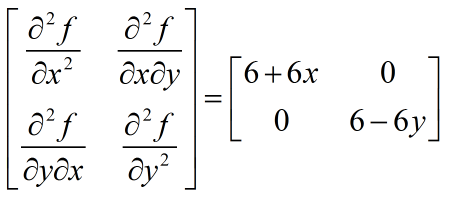Hessian矩陣判定極值之MATLAB實現符號解
阿新 • • 發佈:2019-02-12
By WC 1.9 .2015
1.Hessian矩陣
其定義如下:
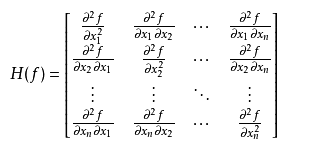
如果函式f在D區域內二階連續可導,那麼黑塞矩陣H(f) 在 D 內為對稱矩陣。原因是:如果函式f連續,則二階偏導數的求導順序沒有區別,即
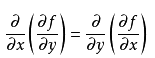
如果該函式的駐點處Hessian陣為正定陣,則在該點取為極小值;如果該函式的駐點處Hessian陣為負定陣,則在該點取為極大值;如果該函式的駐點處Hessian陣為不定陣,則在該點不是極值點。
附錄:
駐點:使下式成立的點
正定陣的判定:
判定定理1:對稱陣A為正定的充分必要條件是:A的特徵值全為正。
特徵值: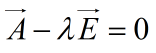
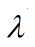
判定定理2:對稱陣A為正定的充分必要條件是:A的各階順序主子式都為正。
順序主子式:對一個三階(3x3)矩陣
a b c
d e f
g h i
一階順序主子式
a
二階順序主子式
a b
d e
三階順序主子式
a b c
d e f
g h i
其他階的與此3階類似
判定定理3:任意陣A為正定的充分必要條件是:A合同於單位陣E
2.Matlab實現
eg:求多元函式f(x,y) = x^3 - y^3 + 3x^2 + 3y^2 - 9x
求得駐點為:(1,0),(1,2),(-3,0),(-3,2)
在求Hessian陣
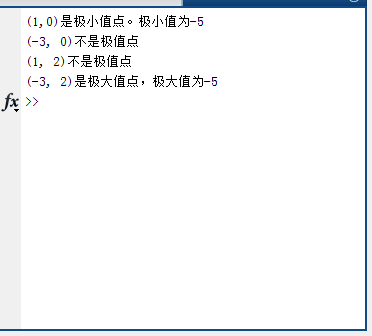
(1) (1,0)使Hessian陣為正定陣(判定定理3),故(1,0)為極小值點,極小值為f(1,0)=-5
(2) (1,2),(-3,0)使Hessian陣為不定陣(判定定理3),非極值點。
(1) (-3,2)使Hessian陣為負定陣(證明請百度),故(-3,2)為極大值點,極大值為f(-3,2)=31。
其圖形為:
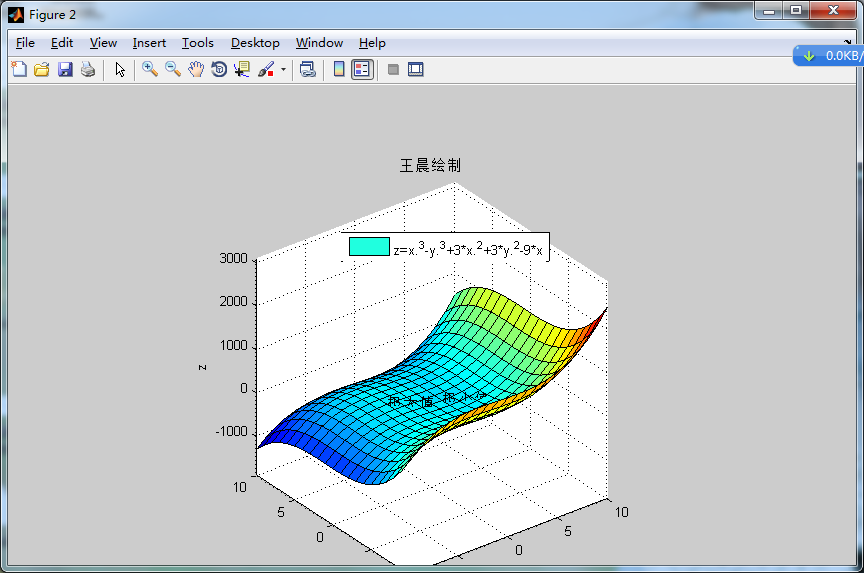
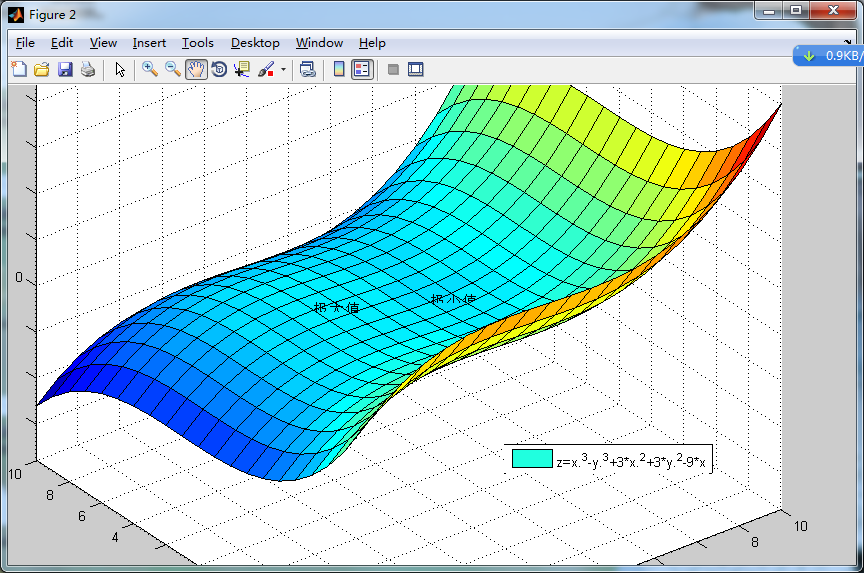
MATLAB程式見如下所示:
clear,clc;close all;
t=-10:1:10;
[x,y]=meshgrid(t,t);
z=x.^3-y.^3+3*x.^2+3*y.^2-9*x;
surf(x,y,z)
%set(gcf,'unit','normalized' 2.MATLAB實現該問題(無約束極值問題)
clc,clear
syms x y f %定義符號物件
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f);%求雅克比矩陣,即一階偏導數
d2f=jacobian(df);%求Hessian矩陣
[xx,yy]=solve(df); %求駐點
xx=int8(xx);yy=int8(yy);%將符號物件轉化為數值型資料
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)}) ; %將xx(i),yy(i)置換x,y帶入d2f中
b=eig(a) ;%求矩陣的特徵值
f=subs(f,{x,y},{xx(i),yy(i)}) ;%求駐點處的極值
f=int8(f);
if all(b>0)
fprintf('(%d,%d)是極小值點。極小值為%d \n',xx(i),yy(i),f);
elseif all(b<0)
fprintf('(%d, %d)是極大值點,極大值為%d \n',xx(i),yy(i),f);
else
fprintf('(%d, %d)不是極值點 \n',xx(i),yy(i));
end
end