最近鄰查詢演算法kd-tree
海量資料最近鄰查詢的kd-tree簡介
利用Octree,為封閉的3D空間建立一個資料結構來管理空間中的每個元素。如此我們可以在 O(log N) 的時間內對這3D空間進行搜尋。
3D空間可以用Octree,2D空間可以用Quadtree(四元樹,概念跟Octree一樣)。那麼4D空間呢?5D空間呢? .... 遇到多維度的空間時,要怎麼去建立一個資料結構來有效管理呢?K-d tree 可以解決這個問題,這是由 Bentley [1] 在 1975年所提出的概念並發表在ACM (Association for Computing Machinery)上。
若有一筆資料 f(x) 佈於 k 維度的空間內,其中 x代表 k 維度的向量,也就是該空間的位置。
本文的主要目的是講一下如何建立k-d tree對特徵點集合進行資料組織和使用k-d tree來進行最近鄰搜尋。
k-d樹(k-dimensional),是一種分割k維資料空間的資料結構(對資料點在k維空間中劃分的一種資料結構),是一種高維索引樹形資料結構。K-D樹是二進位制空間分割樹的特殊的情況。其實,Kd-樹是一種平衡二叉樹。
K-d tree 是一個二元樹(binary tree),在此樹中除了樹葉外,每一節點皆代表此k維度空間中的某一點,且能平分某一維度的某個子平面空間。
K-d tree 也具有平衡的特質(balanced),即任兩樹葉的高度差皆不超過1。
主要應用於多維空間關鍵資料的搜尋(如:範圍搜尋和最近鄰搜尋)。常用於在大規模的高維資料空間進行最近鄰查詢(Nearest Neighbor)和近似最近鄰查詢(Approximate Nearest Neighbor),例如影象檢索和識別中的高維影象特徵向量的K近鄰查詢與匹配。
Kd-Tree與一維二叉查詢樹之間的區別
二叉查詢樹:資料存放在樹中的每個結點(根結點、中間結點、葉子結點)中;
Kd-Tree:資料只存放在葉子結點,而根結點和中間結點存放一些空間劃分資訊(例如劃分維度、劃分值);{Note: 後面的示例從示例1起,對應的kdtree都將資料寫在了劃分結點上,其實只是示意,實際並未如此儲存!}
應用背景
SIFT演算法中做特徵點匹配的時候就會利用到k-d樹。而特徵點匹配實際上就是一個通過距離函式在高維向量之間進行相似性檢索的問題。針對如何快速而準確地找到查詢點的近鄰,現在提出了很多高維空間索引結構和近似查詢的演算法,k-d樹就是其中一種。
索引結構中相似性查詢有兩種基本的方式:一種是範圍查詢(range searches),另一種是K近鄰查詢(K-neighbor searches)。範圍查詢就是給定查詢點和查詢距離的閾值,從資料集中找出所有與查詢點距離小於閾值的資料;K近鄰查詢是給定查詢點及正整數K,從資料集中找到距離查詢點最近的K個數據,當K=1時,就是最近鄰查詢(nearest neighbor searches)。
特徵匹配運算元大致可以分為兩類。一類是線性掃描法,即將資料集中的點與查詢點逐一進行距離比較,也就是窮舉,缺點很明顯,就是沒有利用資料集本身蘊含的任何結構資訊,搜尋效率較低,第二類是建立資料索引,然後再進行快速匹配。因為實際資料一般都會呈現出簇狀的聚類形態,通過設計有效的索引結構可以大大加快檢索的速度。索引樹屬於第二類,其基本思想就是對搜尋空間進行層次劃分。根據劃分的空間是否有混疊可以分為Clipping和Overlapping兩種。前者劃分空間沒有重疊,其代表就是k-d樹;後者劃分空間相互有交疊,其代表為R樹。(這裡只介紹k-d樹)
為了更好的引出k-d tree,先講一講最近鄰搜尋。
最近鄰搜尋
最近鄰的數學形式的定義
給定一個多維空間![]() ,把
,把![]() 中的一個向量成為一個樣本點或資料點。
中的一個向量成為一個樣本點或資料點。![]() 中樣本點的有限集合稱為樣本集。給定樣本集E,和一個樣本點d,d的最近鄰就是任何樣本點d’∈E滿足None-nearer(E,d,d’)。
中樣本點的有限集合稱為樣本集。給定樣本集E,和一個樣本點d,d的最近鄰就是任何樣本點d’∈E滿足None-nearer(E,d,d’)。
None-nearer如下定義:
![]()
上面的公式中距離度量是歐式距離,當然也可以是任何其他Lp-norm。
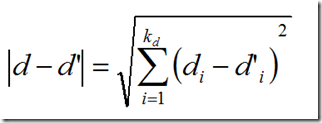
其中di是向量d的第i個分量。
樸素最近鄰搜尋
現在再來說最近鄰搜尋,如何找到一個這樣的d’,它離d的距離在E中是最近的。
很容易想到的一個方法就是線性掃描,也稱為窮舉搜尋,依次計算樣本集E中每個樣本點到d的距離,然後取最小距離的那個點。這個方法又稱為樸素最近鄰搜尋。當樣本集E較大時(在物體識別的問題中,可能有數千個甚至數萬個SIFT特徵點),顯然這種策略是非常耗時的。
k-d tree的簡介及表示
表示
因為實際資料一般都會呈現簇狀的聚類形態,因此我們想到建立資料索引,然後再進行快速匹配。索引樹是一種樹結構索引方法,其基本思想是對搜尋空間進行層次劃分。k-d tree是索引樹中的一種典型的方法。
k-d tree是英文K-dimension tree的縮寫,是對資料點在k維空間中劃分的一種資料結構。k-d tree實際上是一種二叉樹。每個結點的內容如下:
| 域名 | 型別 | 描述 |
| dom_elt | kd維的向量 | kd維空間中的一個樣本點 |
| split | 整數 | 分裂維的序號,也是垂直於分割超面的方向軸序號 |
| left | kd-tree | 由位於該結點分割超面左子空間內所有資料點構成的kd-tree |
| right | kd-tree | 由位於該結點分割超面右子空間內所有資料點構成的kd-tree |
樣本集E由k-d tree的結點的集合表示,每個結點表示一個樣本點,dom_elt就是表示該樣本點的向量。該樣本點根據結點的分割超平面將樣本空間分為兩個子空間。左子空間中的樣本點集合由左子樹left表示,右子空間中的樣本點集合由右子樹right表示。分割超平面是一個通過點dom_elt並且垂直於split所指示的方向軸的平面。
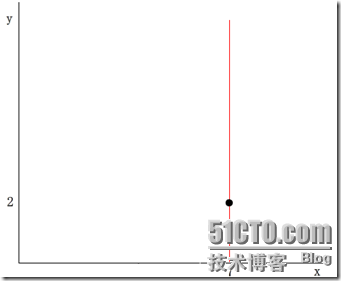
舉個簡單的例子,在二維的情況下,一個樣本點可以由二維向量(x,y)表示,其中令x維的序號為0,y維的序號為1。假設一個結點的dom_elt為(7,2) ,split的取值為0,那麼分割超面就是x=dom_elt(0)=7,它垂直與x軸且過點(7,2),如下圖所示:
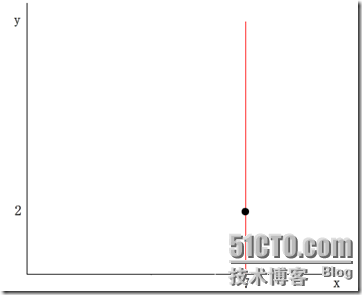
(紅線代表分割超平面)
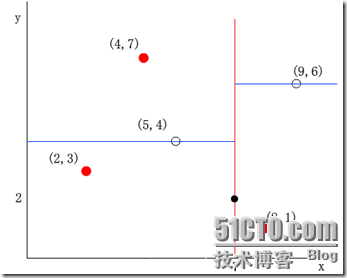
於是其他資料點的x維(第split=0維)如果小於7,則被分配到左子空間;若大於7,則被分配到右子空間。例如,(5,4)被分配到左子空間,(9,6)被分配到右子空間。如下圖所示:
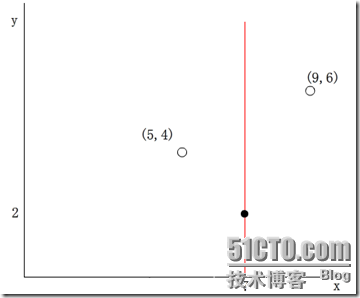
從上面的表也可以看出k-d tree本質上是一種二叉樹,因此k-d tree的構建是一個逐級展開的遞迴過程。
並且從這個過程中可知,內部節點都在分割面上,而葉子節點都在某個分割區域中。
kdtree的構建 過程
怎樣構造一棵Kd-tree?
對於Kd-tree這樣一棵二叉樹,我們首先需要確定怎樣劃分左子樹和右子樹,即一個K維資料是依據什麼被劃分到左子樹或右子樹的。
在構造1維BST樹時,一個1維資料根據其與樹的根結點和中間結點進行大小比較的結果來決定是劃分到左子樹還是右子樹,同理,我們也可以按照這樣的方式,將一個K維資料與Kd-tree的根結點和中間結點進行比較,只不過不是對K維資料進行整體的比較,而是選擇某一個維度Di,然後比較兩個K維數在該維度Di上的大小關係,即每次選擇一個維度Di來對K維資料進行劃分,相當於用一個垂直於該維度Di的超平面將K維資料空間一分為二,平面一邊的所有K維資料在Di維度上的值小於平面另一邊的所有K維資料對應維度上的值。也就是說,我們每選擇一個維度進行如上的劃分,就會將K維資料空間劃分為兩個部分,如果我們繼續分別對這兩個子K維空間進行如上的劃分,又會得到新的子空間,對新的子空間又繼續劃分,重複以上過程直到每個子空間都不能再劃分為止。
Kd-Tree的構建演算法
(1) 在K維資料集合中選擇具有最大方差的維度k,然後在該維度上選擇中值m為pivot對該資料集合進行劃分,得到兩個子集合;同時建立一個樹結點node,用於儲存<k, m>;
(2)對兩個子集合重複(1)步驟的過程,直至所有子集合都不能再劃分為止;如果某個子集合不能再劃分時,則將該子集合中的資料儲存到葉子結點(leaf node)。
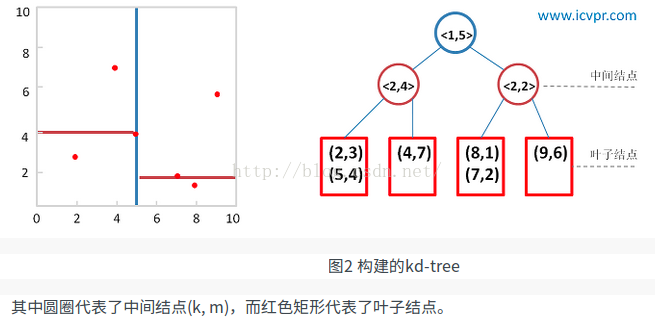
給定二維資料集合:(2,3), (5,4), (9,6), (4,7), (8,1), (7,2),利用上述演算法構建一棵Kd-tree。左圖是Kd-tree對應二維資料集合的一個空間劃分,右圖是構建的一棵Kd-tree。
1)k-d tree[5]
把n維特徵的觀測例項放到n維空間中,k-d tree每次通過某種演算法選擇一個特徵(座標軸),以它的某一個值作為分界做超平面,把當前所有觀測點分為兩部分,然後對每一個部分使用同樣的方法,直到達到某個條件為止。
上面的表述中,有幾個地方下面將會詳細說明:(1)選擇特徵(座標軸)的方法 (2)以該特徵的哪一個為界 (3)達到什麼條件演算法結束。
(1)選擇特徵的方法
計算當前觀測點集合中每個特徵的方差,選擇方差最大的一個特徵,然後畫一個垂直於這個特徵的超平面將所有觀測點分為兩個集合。
(2)以該特徵的哪一個值為界 即垂直選擇座標軸的超平面的具體位置。
第一種是以各個點的方差的中值(median)為界。這樣會使建好的樹非常地平衡,會均勻地分開一個集合。這樣做的問題是,如果點的分佈非常不好地偏斜的,選擇中值會造成連續相同方向的分割,形成細長的超矩形(hyperrectangles)。
替代的方法是計算這些點該座標軸的平均值,選擇距離這個平均值最近的點作為超平面與這個座標軸的交點。這樣這個樹不會完美地平衡,但區域會傾向於正方地被劃分,連續的分割更有可能在不同方向上發生。
(3)達到什麼條件演算法結束
實際中,不用指導葉子結點只包含兩個點時才結束演算法。你可以設定一個預先設定的最小值,當這個最小值達到時結束演算法。

圖 6 一個k-d tree劃分二維空間
圖6中,星號標註的是目標點,我們在k-d tree中找到這個點所處的區域後,依次計算此區域包含的點的距離,找出最近的一個點(黑色點),如果在其他region中還包含更近的點則一定在以這兩個點為半徑的圓中。假設這個圓如圖中所示包含其他區域。先看這個區域兄弟結點對應區域,與圓不重疊;再看其雙親結點的兄弟結點對應區域。從它的子結點對應區域中尋找(圖中確實與這個雙親結點的兄弟結點的子結點對應區域重疊了)。在其中找是否有更近的結點。
k-d tree的優勢是可以遞增更新。新的觀測點可以不斷地加入進來。找到新觀測點應該在的區域,如果它是空的,就把它新增進去,否則,沿著最長的邊分割這個區域來保持接近正方形的性質。這樣會破壞樹的平衡性,同時讓區域不利於找最近鄰。我們可以當樹的深度到達一定值時重建這棵樹。
分裂結點選擇程式
分裂結點的選擇通常有多種方法,最常用的是一種方法是:對於所有的樣本點,統計它們在每個維上的方差,挑選出方差中的最大值,對應的維就是split域的值。資料方差最大表明沿該維度資料點分散得比較開,這個方向上進行資料分割可以獲得最好的解析度;然後再將所有樣本點按其第split維的值進行排序,位於正中間的那個資料點選為分裂結點的dom_elt域。
每次對子空間的劃分時,怎樣確定在哪個維度上進行劃分?
最簡單的方法就是輪著來,即如果這次選擇了在第i維上進行資料劃分,那下一次就在第j(j≠i)維上進行劃分,例如:j = (i mod k) + 1。想象一下我們切豆腐時,先是豎著切一刀,切成兩半後,再橫著來一刀,就得到了很小的方塊豆腐。可是“輪著來”的方法是否可以很好地解決問題呢?再次想象一下,我們現在要切的是一根木條,按照“輪著來”的方法先是豎著切一刀,木條一分為二,乾淨利落,接下來就是再橫著切一刀,這個時候就有點考驗刀法了,如果木條的直徑(橫截面)較大,還可以下手,如果直徑較小,就沒法往下切了。因此,如果K維資料的分佈像上面的豆腐一樣,“輪著來”的切分方法是可以奏效,但是如果K維度上資料的分佈像木條一樣,“輪著來”就不好用了。因此,還需要想想其他的切法。
如果一個K維資料集合的分佈像木條一樣,那就是說明這K維資料在木條較長方向代表的維度上,這些資料的分佈散得比較開,數學上來說,就是這些資料在該維度上的方差(invariance)比較大,換句話說,正因為這些資料在該維度上分散的比較開,我們就更容易在這個維度上將它們劃分開,因此,這就引出了我們選擇維度的另一種方法:最大方差法(max invarince),即每次我們選擇維度進行劃分時,都選擇具有最大方差維度。
在某個維度上進行劃分時,怎樣確保在這一維度上的劃分得到的兩個子集合的數量儘量相等,即左子樹和右子樹中的結點個數儘量相等?
假設當前我們按照最大方差法選擇了在維度i上進行K維資料集S的劃分,此時我們需要在維度i上將K維資料集合S劃分為兩個子集合A和B,子集合A中的資料在維度i上的值都小於子集合B中。首先考慮最簡單的劃分法,即選擇第一個數作為比較物件(即劃分軸,pivot),S中剩餘的其他所有K維資料都跟該pivot在維度i上進行比較,如果小於pivot則劃A集合,大於則劃入B集合。把A集合和B集合分別看做是左子樹和右子樹,那麼我們在構造一個二叉樹的時候,當然是希望它是一棵儘量平衡的樹,即左右子樹中的結點個數相差不大。而A集合和B集合中資料的個數顯然跟pivot值有關,因為它們是跟pivot比較後才被劃分到相應的集合中去的。好了,現在的問題就是確定pivot了。給定一個數組,怎樣才能得到兩個子陣列,這兩個陣列包含的元素個數差不多且其中一個子陣列中的元素值都小於另一個子陣列呢?方法很簡單,找到陣列中的中值(即中位數,median),然後將陣列中所有元素與中值進行比較,就可以得到上述兩個子陣列。同樣,在維度i上進行劃分時,pivot就選擇該維度i上所有資料的中值,這樣得到的兩個子集合資料個數就基本相同了。
kdtree最近鄰查詢的演算法過程
構建好一棵Kd-Tree後,下面給出利用Kd-Tree進行最近鄰查詢的演算法:
(1)將查詢資料Q從根結點開始,按照Q與各個結點的比較結果向下訪問Kd-Tree,直至達到葉子結點。
其中Q與結點的比較指的是將Q對應於結點中的k維度上的值與m進行比較,若Q(k) < m,則訪問左子樹,否則訪問右子樹。達到葉子結點時,計算Q與葉子結點上儲存的資料之間的距離,記錄下最小距離對應的資料點,記為當前“最近鄰點”Pcur和最小距離Dcur。
(2)進行回溯(Backtracking)操作,該操作是為了找到離Q更近的“最近鄰點”。即判斷未被訪問過的分支裡是否還有離Q更近的點,它們之間的距離小於Dcur。
如果Q與其父結點下的未被訪問過的分支之間的距離小於Dcur,則認為該分支中存在離P更近的資料,進入該結點,進行(1)步驟一樣的查詢過程,如果找到更近的資料點,則更新為當前的“最近鄰點”Pcur,並更新Dcur。如果Q與其父結點下的未被訪問過的分支之間的距離大於Dcur,則說明該分支內不存在與Q更近的點。
回溯的判斷過程是從下往上進行的,直到回溯到根結點時已經不存在與P更近的分支為止。
怎樣判斷未被訪問過的樹分支Branch裡是否還有離Q更近的點?
從幾何空間上來看,就是判斷以Q為中心center和以Dcur為半徑Radius的超球面(Hypersphere)與樹分支Branch代表的超矩形(Hyperrectangle)之間是否相交。
在實現中,我們可以有兩種方式來求Q與樹分支Branch之間的距離。第一種是在構造樹的過程中,就記錄下每個子樹中包含的所有資料在該子樹對應的維度k上的邊界引數[min, max];第二種是在構造樹的過程中,記錄下每個子樹所在的分割維度k和分割值m,(k, m),Q與子樹的距離則為|Q(k) - m|。
kdtree演算法實現
構建kd-tree演算法的虛擬碼
1
構建k-d樹的偽碼
| 演算法:構建k-d樹(createKDTree) |
| 輸入:資料點集Data-set和其所在的空間Range |
| 輸出:Kd,型別為k-d tree |
| 1.If Data-set為空,則返回空的k-d tree |
| 2.呼叫節點生成程式:(1)確定split域:對於所有描述子資料(特徵向量),統計它們在每個維上的資料方差。以SURF特徵為例,描述子為64維,可計算64個方差。挑選出最大值,對應的維就是split域的值。資料方差大表明沿該座標軸方向上的資料分散得比較開,在這個方向上進行資料分割有較好的解析度;(2)確定Node-data域:資料點集Data-set按其第split域的值排序。位於正中間的那個資料點被選為Node-data。此時新的Data-set' = Data-set\Node-data(除去其中Node-data這一點)。 |
| 3.dataleft = {d屬於Data-set' && d[split] ≤ Node-data[split]}Left_Range = {Range && dataleft} dataright = {d屬於Data-set' && d[split] > Node-data[split]}Right_Range = {Range && dataright} |
| 4.left = 由(dataleft,Left_Range)建立的k-d tree,即遞迴呼叫createKDTree(dataleft,Left_Range)。 並設定left的parent域為Kd;right = 由(dataright,Right_Range)建立的k-d tree,即呼叫createKDTree(dataright,Right_Range)。 並設定right的parent域為Kd。 |
演算法:createKDTree 構建一棵k-d tree
輸入:exm_set 樣本集
輸出 : Kd, 型別為kd-tree
1. 如果exm_set是空的,則返回空的kd-tree
2.呼叫分裂結點選擇程式(輸入是exm_set),返回兩個值
dom_elt:= exm_set中的一個樣本點
split := 分裂維的序號
3.exm_set_left = {exm∈exm_set – dom_elt && exm[split] <= dom_elt[split]}
exm_set_right = {exm∈exm_set – dom_elt && exm[split] > dom_elt[split]}
4.left = createKDTree(exm_set_left)
right = createKDTree(exm_set_right)
k-d tree的最近鄰搜尋演算法
如前所述,在k-d tree樹中進行資料的k近鄰搜尋是特徵匹配的重要環節,其目的是檢索在k-d tree中與待查詢點距離最近的k個數據點。
最近鄰搜尋是k近鄰的特例,也就是1近鄰。將1近鄰改擴充套件到k近鄰非常容易。下面介紹最簡單的k-d tree最近鄰搜尋演算法。
基本的思路很簡單:首先通過二叉樹搜尋(比較待查詢節點和分裂節點的分裂維的值,小於等於就進入左子樹分支,等於就進入右子樹分支直到葉子結點),順著“搜尋路徑”很快能找到最近鄰的近似點,也就是與待查詢點處於同一個子空間的葉子結點;然後再回溯搜尋路徑,並判斷搜尋路徑上的結點的其他子結點空間中是否可能有距離查詢點更近的資料點,如果有可能,則需要跳到其他子結點空間中去搜索(將其他子結點加入到搜尋路徑)。重複這個過程直到搜尋路徑為空。下面給出k-d tree最近鄰搜尋的虛擬碼:
演算法:kdtreeFindNearest /* k-d tree的最近鄰搜尋 */
輸入:Kd /* k-d tree型別*/
target /* 待查詢資料點 */
輸出 : nearest /* 最近鄰資料結點 */
dist /* 最近鄰和查詢點的距離 */
1. 如果Kd是空的,則設dist為無窮大返回
2. 向下搜尋直到葉子結點
pSearch = &Kd
while(pSearch != NULL) {
pSearch加入到search_path中;
if(target[pSearch->split] <= pSearch->dom_elt[pSearch->split]) /* 如果小於就進入左子樹 */
{
pSearch = pSearch->left;
}
else {
pSearch = pSearch->right;
}
}
取出search_path最後一個賦給nearest
dist = Distance(nearest, target);
3. 回溯搜尋路徑
while(search_path不為空) {
取出search_path最後一個結點賦給pBack
if(pBack->left為空 && pBack->right為空) /* 如果pBack為葉子結點 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) ) {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
}
else {
s = pBack->split;
if( abs(pBack->dom_elt[s] - target[s]) < dist) /* 如果以target為中心的圓(球或超球),半徑為dist的圓與分割超平面相交, 那麼就要跳到另一邊的子空間去搜索 */
{
if( Distance(nearest, target) > Distance(pBack->dom_elt, target) ) {
nearest = pBack->dom_elt;
dist = Distance(pBack->dom_elt, target);
}
if(target[s] <= pBack->dom_elt[s]) /* 如果target位於pBack的左子空間,那麼就要跳到右子空間去搜索 */
pSearch = pBack->right;
else
pSearch = pBack->left; /* 如果target位於pBack的右子空間,那麼就要跳到左子空間去搜索 */
if(pSearch != NULL)
pSearch加入到search_path中
}
}
}
k-d tree的構建過程及搜尋例項
示例1
假設樣本集為:{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}。構建過程如下:
(1)確定split域,6個數據點在x,y維度上的資料方差分別為39, 28.63。在x軸上方差最大,所以split域值為0(x維的序號為0)
(2)確定分裂節點,根據x維上的值將資料排序,則6個數據點再排序後位於中間的那個資料點為(7,2),該結點就是分割超平面就是通過(7,2)並垂直於split=0(x)軸的直線x=7
(3)左子空間和右子空間,分割超面x=7將整個空間氛圍兩部分,x<=7的部分為左子空間,包含3個數據點{(2,3), (5,4), (4,7)};另一部分為右子空間,包含2個數據點{(9,6), (8,1)}。如下圖所示
(4)分別對左子空間中的資料點和右子空間中的資料點重複上面的步驟構建左子樹和右子樹直到經過劃分的子樣本集為空。下面的圖從左至右從上至下顯示了構建這棵二叉樹的所有步驟:


示例2
假設有六個二維資料點 = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},資料點位於二維空間中。為了能有效的找到最近鄰,Kd-樹採用分而治之的思想,即將整個空間劃分為幾個小部分。六個二維資料點生成的Kd-樹的圖為:

示例3
假設我們的k-d tree就是上面通過樣本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}建立的。將上面的圖轉化為樹形圖的樣子如下:
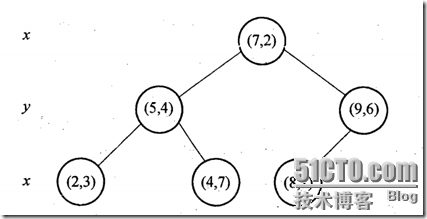
我們來查詢點(2.1,3.1),在(7,2)點測試到達(5,4),在(5,4)點測試到達(2,3),然後search_path中的結點為<(7,2), (5,4), (2,3)>,從search_path中取出(2,3)作為當前最佳結點nearest, dist為0.141;
然後回溯至(5,4),以(2.1,3.1)為圓心,以dist=0.141為半徑畫一個圓,並不和超平面y=4相交,如下圖,所以不必跳到結點(5,4)的右子空間去搜索,因為右子空間中不可能有更近樣本點了。
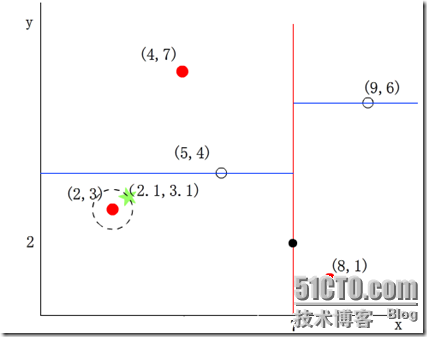
於是在回溯至(7,2),同理,以(2.1,3.1)為圓心,以dist=0.141為半徑畫一個圓並不和超平面x=7相交,所以也不用跳到結點(7,2)的右子空間去搜索。
至此,search_path為空,結束整個搜尋,返回nearest(2,3)作為(2.1,3.1)的最近鄰點,最近距離為0.141。
示例4
再舉一個稍微複雜的例子,我們來查詢點(2,4.5),在(7,2)處測試到達(5,4),在(5,4)處測試到達(4,7),然後search_path中的結點為<(7,2), (5,4), (4,7)>,從search_path中取出(4,7)作為當前最佳結點nearest, dist為3.202;
然後回溯至(5,4),以(2,4.5)為圓心,以dist=3.202為半徑畫一個圓與超平面y=4相交,如下圖,所以需要跳到(5,4)的左子空間去搜索。所以要將(2,3)加入到search_path中,現在search_path中的結點為<(7,2), (2, 3)>;另外,(5,4)與(2,4.5)的距離為3.04 < dist = 3.202,所以將(5,4)賦給nearest,並且dist=3.04。
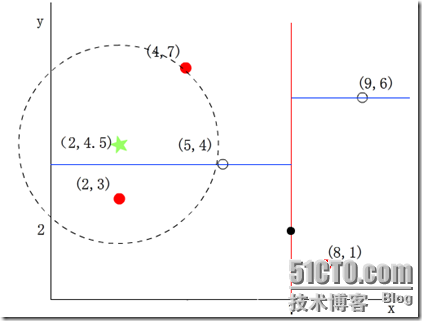
回溯至(2,3),(2,3)是葉子節點,直接平判斷(2,3)是否離(2,4.5)更近,計算得到距離為1.5,所以nearest更新為(2,3),dist更新為(1.5)
回溯至(7,2),同理,以(2,4.5)為圓心,以dist=1.5為半徑畫一個圓並不和超平面x=7相交, 所以不用跳到結點(7,2)的右子空間去搜索。
至此,search_path為空,結束整個搜尋,返回nearest(2,3)作為(2,4.5)的最近鄰點,最近距離為1.5。
兩次搜尋的返回的最近鄰點雖然是一樣的,但是搜尋(2, 4.5)的過程要複雜一些,因為(2, 4.5)更接近超平面。研究表明,當查詢點的鄰域與分割超平面兩側的空間都產生交集時,回溯的次數大大增加。最壞的情況下搜尋N個結點的k維kd-tree所花費的時間為:
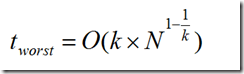
複雜度分析
對於擁有n個已知點的kD-Tree,其複雜度如下:
構建:O(log2n)
插入:O(log n)
刪除:O(log n)
查詢:O(n1-1/k+m) m---每次要搜尋的最近點個數
把最鄰近點演算法擴充套件成K-最鄰近點演算法
...
k-d tree的擴充套件
Kd-tree with BBF
由於大量回溯會導致kd-tree最近鄰搜尋的效能大大下降,因此研究人員也提出了改進的k-d tree近鄰搜尋。
其中一個比較著名的就是 Best-Bin-First,它通過設定優先順序佇列和執行超時限定來獲取近似的最近鄰,有效地減少回溯的次數。
Kd-tree在維度較小時(例如:K≤30),演算法的查詢效率很高,然而當Kd-tree用於對高維資料(例如:K≥100)進行索引和查詢時,就面臨著維數災難(curse of dimension)問題,查詢效率會隨著維度的增加而迅速下降。通常,實際應用中,我們常常處理的資料都具有高維的特點,例如在影象檢索和識別中,每張影象通常用一個幾百維的向量來表示,每個特徵點的區域性特徵用一個高維向量來表徵(例如:128維的SIFT特徵)。因此,為了能夠讓Kd-tree滿足對高維資料的索引,Jeffrey S. Beis和David G. Lowe提出了一種改進演算法——Kd-tree with BBF(Best Bin First),該演算法能夠實現近似K近鄰的快速搜尋,在保證一定查詢精度的前提下使得查詢速度較快。
在介紹BBF演算法前,我們先來看一下原始Kd-tree是為什麼在低維空間中有效而到了高維空間後查詢效率就會下降。在原始kd-tree的最近鄰查詢演算法中(第一節中介紹的演算法),為了能夠找到查詢點Q在資料集合中的最近鄰點,有一個重要的操作步驟:回溯,該步驟是在未被訪問過的且與Q的超球面相交的子樹分支中查詢可能存在的最近鄰點。隨著維度K的增大,與Q的超球面相交的超矩形(子樹分支所在的區域)就會增加,這就意味著需要回溯判斷的樹分支就會更多,從而演算法的查詢效率便會下降很大。
一個很自然的思路是:既然kd-tree演算法在高維空間中是由於過多的回溯次數導致演算法查詢效率下降的話,我們就可以限制查詢時進行回溯的次數上限,從而避免查詢效率下降。這樣做有兩個問題需要解決:1)最大回溯次數怎麼確定?2)怎樣保證在最大回溯次數內找到的最近鄰比較接近真實最近鄰,即查詢準確度不能下降太大。
K值的選擇
除了上述1.2節如何定義鄰居的問題之外,還有一個選擇多少個鄰居,即K值定義為多大的問題。不要小看了這個K值選擇問題,因為它對K近鄰演算法的結果會產生重大影響。如李航博士的一書「統計學習方法」上所說:
如果選擇較小的K值,就相當於用較小的領域中的訓練例項進行預測,“學習”近似誤差會減小,只有與輸入例項較近或相似的訓練例項才會對預測結果起作用,與此同時帶來的問題是“學習”的估計誤差會增大,換句話說,K值的減小就意味著整體模型變得複雜,容易發生過擬合;
如果選擇較大的K值,就相當於用較大領域中的訓練例項進行預測,其優點是可以減少學習的估計誤差,但缺點是學習的近似誤差會增大。這時候,與輸入例項較遠(不相似的)訓練例項也會對預測器作用,使預測發生錯誤,且K值的增大就意味著整體的模型變得簡單。
K=N,則完全不足取,因為此時無論輸入例項是什麼,都只是簡單的預測它屬於在訓練例項中最多的累,模型過於簡單,忽略了訓練例項中大量有用資訊。
在實際應用中,K值一般取一個比較小的數值,例如採用交叉驗證法(簡單來說,就是一部分樣本做訓練集,一部分做測試集)來選擇最優的K值。
k-d tree的實現庫
虛擬碼:
python:
c/c++:
[kdtree A simple C library for working with KD-Trees]
java:
Paper
[1] Multidimensional binary search trees used for associative searching*
[2] Shape indexing using approximate nearest-neighbour search in high-dimensional spaces
Tutorial
[1] [An intoductory tutorial on kd-trees Andrew W.Moore]
[2] Nearest-Neighbor Methods in Learning and Vision: Theory and Practice