本文介紹一種用於高維空間中的快速最近鄰和近似最近鄰查詢技術——Kd-Tree（Kd樹）。Kd-Tree，即K-dimensional tree，是一種高維索引樹形資料結構，常用於在大規模的高維資料空間進行最近鄰查詢(Nearest Neighbor)和近似最近鄰查詢(Approximate Nearest Neighbor)，例如影象檢索和識別中的高維影象特徵向量的K近鄰查詢與匹配。本文首先介紹Kd-Tree的基本原理，然後對基於BBF的近似查詢方法進行介紹，最後給出一些參考文獻和開源實現程式碼。

一、Kd-tree

 Kd-Tree，即K-dimensional tree，是一棵二叉樹，樹中儲存的是一些K維資料。在一個K維資料集合上構建一棵Kd-Tree代表了對該K維資料集合構成的K維空間的一個劃分，即樹中的每個結點就對應了一個K維的超矩形區域（Hyperrectangle）。

在介紹Kd-tree的相關演算法前，我們先回顧一下二叉查詢樹（Binary Search Tree）的相關概念和演算法。

二叉查詢樹（Binary Search Tree，BST），是具有如下性質的二叉樹（來自wiki）：

1）若它的左子樹不為空，則左子樹上所有結點的值均小於它的根結點的值；

2）若它的右子樹不為空，則右子樹上所有結點的值均大於它的根結點的值；

3）它的左、右子樹也分別為二叉排序樹；

例如，圖1中是一棵二叉查詢樹，其滿足BST的性質。

給定一個1維資料集合，怎樣構建一棵BST樹呢？根據BST的性質就可以建立，即將資料點一個一個插入到BST樹中，插入後的樹仍然是BST樹，即根結點的左子樹中所有結點的值均小於根結點的值，而根結點的右子樹中所有結點的值均大於根結點的值。

將一個1維資料集用一棵BST樹儲存後，當我們想要查詢某個資料是否位於該資料集合中時，只需要將查詢資料與結點值進行比較然後選擇對應的子樹繼續往下查詢即可，查詢的平均時間複雜度為：O(logN)，最壞的情況下是O(N)。

如果我們要處理的物件集合是一個K維空間中的資料集，那麼是否也可以構建一棵類似於1維空間中的二叉查詢樹呢？答案是肯定的，只不過推廣到K維空間後，建立二叉樹和查詢二叉樹的演算法會有一些相應的變化（後面會介紹到兩者的區別），這就是下面我們要介紹的Kd-tree演算法。

怎樣構造一棵Kd-tree？

建樹必須遵循兩個準則：

1.建立的樹應當儘量平衡，樹越平衡代表著分割得越平均，搜尋的時間也就是越少。

2.最大化鄰域搜尋的剪枝機會。

對於Kd-tree這樣一棵二叉樹，我們首先需要確定怎樣劃分左子樹和右子樹，即一個K維資料是依據什麼被劃分到左子樹或右子樹的。

在構造1維BST樹時，一個1維資料根據其與樹的根結點和中間結點進行大小比較的結果來決定是劃分到左子樹還是右子樹，同理，我們也可以按照這樣的方式，將一個K維資料與Kd-tree的根結點和中間結點進行比較，只不過不是對K維資料進行整體的比較，而是選擇某一個維度Di，然後比較兩個K維數在該維度Di上的大小關係，即每次選擇一個維度Di來對K維資料進行劃分，相當於用一個垂直於該維度Di的超平面將K維資料空間一分為二，平面一邊的所有K維資料在Di維度上的值小於平面另一邊的所有K維資料對應維度上的值。也就是說，我們每選擇一個維度進行如上的劃分，就會將K維資料空間劃分為兩個部分，如果我們繼續分別對這兩個子K維空間進行如上的劃分，又會得到新的子空間，對新的子空間又繼續劃分，重複以上過程直到每個子空間都不能再劃分為止。以上就是構造Kd-Tree的過程，上述過程中涉及到兩個重要的問題：1）每次對子空間的劃分時，怎樣確定在哪個維度上進行劃分；2）在某個維度上進行劃分時，怎樣確保在這一維度上的劃分得到的兩個子集合的數量儘量相等，即左子樹和右子樹中的結點個數儘量相等。

問題1： 每次對子空間的劃分時，怎樣確定在哪個維度上進行劃分？

答：最大方差法

最簡單的方法就是輪著來，即如果這次選擇了在第i維上進行資料劃分，那下一次就在第j(j≠i)維上進行劃分，例如：j = (i mod k) + 1。想象一下我們切豆腐時，先是豎著切一刀，切成兩半後，再橫著來一刀，就得到了很小的方塊豆腐。

可是“輪著來”的方法是否可以很好地解決問題呢？再次想象一下，我們現在要切的是一根木條，按照“輪著來”的方法先是豎著切一刀，木條一分為二，乾淨利落，接下來就是再橫著切一刀，這個時候就有點考驗刀法了，如果木條的直徑（橫截面）較大，還可以下手，如果直徑較小，就沒法往下切了。因此，如果K維資料的分佈像上面的豆腐一樣，“輪著來”的切分方法是可以奏效，但是如果K維度上資料的分佈像木條一樣，“輪著來”就不好用了。因此，還需要想想其他的切法。

如果一個K維資料集合的分佈像木條一樣，那就是說明這K維資料在木條較長方向代表的維度上，這些資料的分佈散得比較開，數學上來說，就是這些資料在該維度上的方差（invariance）比較大，換句話說，正因為這些資料在該維度上分散的比較開，我們就更容易在這個維度上將它們劃分開，因此，這就引出了我們選擇維度的另一種方法：最大方差法（max invarince），即每次我們選擇維度進行劃分時，都選擇具有最大方差維度。（最大方差法在本文最後有說明）

問題2：在某個維度上進行劃分時，怎樣確保在這一維度上的劃分得到的兩個子集合的數量儘量相等，即左子樹和右子樹中的結點個數儘量相等？

答：選擇pivot，即選擇該維度上所有點的中值

假設當前我們按照最大方差法選擇了在維度i上進行K維資料集S的劃分，此時我們需要在維度i上將K維資料集合S劃分為兩個子集合A和B，子集合A中的資料在維度i上的值都小於子集合B中。首先考慮最簡單的劃分法，即選擇第一個數作為比較物件（即劃分軸，pivot），S中剩餘的其他所有K維資料都跟該pivot在維度i上進行比較，如果小於pivot則劃A集合，大於則劃入B集合。把A集合和B集合分別看做是左子樹和右子樹，那麼我們在構造一個二叉樹的時候，當然是希望它是一棵儘量平衡的樹，即左右子樹中的結點個數相差不大。而A集合和B集合中資料的個數顯然跟pivot值有關，因為它們是跟pivot比較後才被劃分到相應的集合中去的。好了，現在的問題就是確定pivot了。給定一個數組，怎樣才能得到兩個子陣列，這兩個陣列包含的元素個數差不多且其中一個子陣列中的元素值都小於另一個子陣列呢？方法很簡單，找到陣列中的中值（即中位數，median），然後將陣列中所有元素與中值進行比較，就可以得到上述兩個子陣列。同樣，在維度i上進行劃分時，pivot就選擇該維度i上所有資料的中值，這樣得到的兩個子集合資料個數就基本相同了。

 解決了上面兩個重要的問題後，就得到了Kd-Tree的構造演算法了。

Kd-Tree的構建演算法：

（1） 在K維資料集合中選擇具有最大方差的維度k，然後在該維度上選擇中值m為pivot對該資料集合進行劃分，得到兩個子集合；同時建立一個樹結點node，用於儲存；

（2）對兩個子集合重複（1）步驟的過程，直至所有子集合都不能再劃分為止；如果某個子集合不能再劃分時，則將該子集合中的資料儲存到葉子結點（leaf node）。

Kd-Tree與一維二叉查詢樹之間的區別：

二叉查詢樹：資料存放在樹中的每個結點（根結點、中間結點、葉子結點）中；

Kd-Tree：資料只存放在葉子結點，而根結點和中間結點存放一些空間劃分資訊（例如劃分維度、劃分值）；

構建好一棵Kd-Tree後，下面給出利用Kd-Tree進行最近鄰查詢的演算法：

（1）將查詢資料Q從根結點開始，按照Q與各個結點的比較結果向下訪問Kd-Tree，直至達到葉子結點。

其中Q與結點的比較指的是將Q對應於結點中的k維度上的值與m進行比較，若Q(k) < m，則訪問左子樹，否則訪問右子樹。達到葉子結點時，計算Q與葉子結點上儲存的資料之間的距離，記錄下最小距離對應的資料點，記為當前“最近鄰點”Pcur和最小距離Dcur。

（2）進行回溯（Backtracking）操作，該操作是為了找到離Q更近的“最近鄰點”。即判斷未被訪問過的分支裡是否還有離Q更近的點，它們之間的距離小於Dcur。

如果Q與其父結點下的未被訪問過的分支之間的距離小於Dcur，則認為該分支中存在離P更近的資料，進入該結點，進行（1）步驟一樣的查詢過程，如果找到更近的資料點，則更新為當前的“最近鄰點”Pcur，並更新Dcur。

如果Q與其父結點下的未被訪問過的分支之間的距離大於Dcur，則說明該分支內不存在與Q更近的點。

回溯的判斷過程是從下往上進行的，直到回溯到根結點時已經不存在與P更近的分支為止。

怎樣判斷未被訪問過的樹分支Branch裡是否還有離Q更近的點？ 

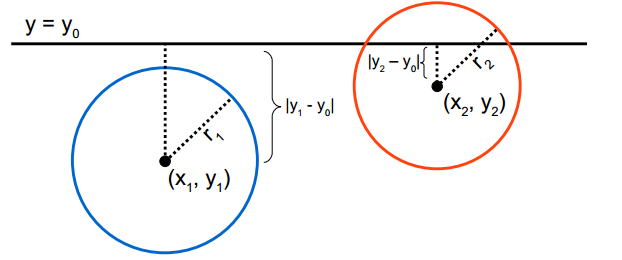
從幾何空間上來看，就是判斷以Q為中心center和以Dcur為半徑Radius的超球面（Hypersphere）與樹分支Branch代表的超矩形（Hyperrectangle）之間是否相交。

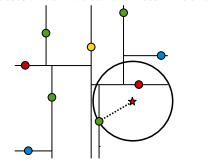
假設標記為星星的點是 test point， 綠色的點是找到的近似點，在回溯過程中，需要用到一個佇列，儲存需要回溯的點，在判斷其他子節點空間中是否有可能有距離查詢點更近的資料點時，做法是以查詢點為圓心，以當前的最近距離為半徑畫圓，這個圓稱為候選超球（candidate hypersphere），如果圓與回溯點的軸相交，則需要將軸另一邊的節點都放到回溯佇列裡面來。如果圓（二維情況就是圓）與回溯點的軸相交，則需要將軸另一邊的節點都放到回溯佇列裡面來。

判斷軸是否與候選超球相交的方法可以參考下圖：

在實現中，我們可以有兩種方式來求Q與樹分支Branch之間的距離。第一種是在構造樹的過程中，就記錄下每個子樹中包含的所有資料在該子樹對應的維度k上的邊界引數[min, max]；第二種是在構造樹的過程中，記錄下每個子樹所在的分割維度k和分割值m，（k, m），Q與子樹的距離則為|Q(k) - m|。

以上就是Kd-tree的構造過程和基於Kd-Tree的最近鄰查詢過程。

二、Kd-tree with BBF

 上一節介紹的Kd-tree在維度較小時（例如：K≤30），演算法的查詢效率很高，然而當Kd-tree用於對高維資料（例如：K≥100）進行索引和查詢時，就面臨著維數災難（curse of dimension）問題，查詢效率會隨著維度的增加而迅速下降。通常，實際應用中，我們常常處理的資料都具有高維的特點，例如在影象檢索和識別中，每張影象通常用一個幾百維的向量來表示，每個特徵點的區域性特徵用一個高維向量來表徵（例如：128維的SIFT特徵）。因此，為了能夠讓Kd-tree滿足對高維資料的索引，Jeffrey S. Beis和David G. Lowe提出了一種改進演算法——Kd-tree with BBF（Best Bin First），該演算法能夠實現近似K近鄰的快速搜尋，在保證一定查詢精度的前提下使得查詢速度較快。

在介紹BBF演算法前，我們先來看一下原始Kd-tree是為什麼在低維空間中有效而到了高維空間後查詢效率就會下降。在原始kd-tree的最近鄰查詢演算法中（第一節中介紹的演算法），為了能夠找到查詢點Q在資料集合中的最近鄰點，有一個重要的操作步驟：回溯，該步驟是在未被訪問過的且與Q的超球面相交的子樹分支中查詢可能存在的最近鄰點。隨著維度K的增大，與Q的超球面相交的超矩形（子樹分支所在的區域）就會增加，這就意味著需要回溯判斷的樹分支就會更多，從而演算法的查詢效率便會下降很大。

一個很自然的思路是：既然kd-tree演算法在高維空間中是由於過多的回溯次數導致演算法查詢效率下降的話，我們就可以限制查詢時進行回溯的次數上限，從而避免查詢效率下降。這樣做有兩個問題需要解決：1）最大回溯次數怎麼確定？2）怎樣保證在最大回溯次數內找到的最近鄰比較接近真實最近鄰，即查詢準確度不能下降太大。

問題1）：最大回溯次數怎麼確定？

最大回溯次數一般人為設定，通常根據在資料集上的實驗結果進行調整。

問題2）：怎樣保證在最大回溯次數內找到的最近鄰比較接近真實最近鄰，即查詢準確度不能下降太大？

限制回溯次數後，如果我們還是按照原來的回溯方法挨個地進行訪問的話，那很顯然最後的查詢結果的精度就很大程度上取決於資料的分佈和回溯次數了。挨個訪問的方法的問題在於認為每個待回溯的樹分支中存在最近鄰的概率是一樣的，所以它對所有的待回溯樹分支一視同仁。實際上，在這些待回溯樹分支中，有些樹分支存在最近鄰的可能性比其他樹分支要高，因為樹分支離Q點之間的距離或相交程度是不一樣的，離Q更近的樹分支存在Q的最近鄰的可能性更高。因此，我們需要區別對待每個待回溯的樹分支，即採用某種優先順序順序來訪問這些待回溯樹分支，使得在有限的回溯次數中找到Q的最近鄰的可能性很高。我們要介紹的BBF演算法正是基於這樣的解決思路，下面我們介紹BBF查詢演算法。

基於BBF的Kd-Tree近似最近鄰查詢演算法

已知：

Q：查詢資料；   KT：已建好的Kd-Tree；

1. 查詢Q的當前最近鄰點P

1）從KT的根結點開始，將Q與中間結點node(k,m)進行比較，根據比較結果選擇某個樹分支Branch（或稱為Bin）；並將未被選擇的另一個樹分支（Unexplored Branch）所在的樹中位置和它跟Q之間的距離一起儲存到一個優先順序佇列中Queue；

2）按照步驟1）的過程，對樹分支Branch進行如上比較和選擇，直至訪問到葉子結點，然後計算Q與葉子結點中儲存的資料之間的距離，並記錄下最小距離D以及對應的資料P。

注：

A、Q與中間結點node(k,m)的比較過程：如果Q(k) > m則選擇右子樹，否則選擇左子樹。

B、優先順序佇列：按照距離從小到大的順序排列。

C、葉子結點：每個葉子結點中儲存的資料的個數可能是一個或多個。

2. 基於BBF的回溯

已知：最大回溯次數BTmax

1）如果當前回溯的次數小於BTmax，且Queue不為空，則進行如下操作：

從Queue中取出最小距離對應的Branch，然後按照1.1步驟訪問該Branch直至達到葉子結點；計算Q與葉子結點中各個資料間距離，如果有比D更小的值，則將該值賦給D，該資料則被認為是Q的當前近似最近鄰點；

2）重複1）步驟，直到回溯次數大於BTmax或Queue為空時，查詢結束，此時得到的資料P和距離D就是Q的近似最近鄰點和它們之間的距離。

最大方差法：（參考：最大方差理論）

在訊號處理中認為訊號具有較大的方差，噪聲有較小的方差，信噪比就是訊號與噪聲的方差比，越大越好。如前面的圖，樣本在橫軸上的投影方差較大，在縱軸上的投影方差較小，那麼認為縱軸上的投影是由噪聲引起的。

因此我們認為，最好的k維特徵是將n維樣本點轉換為k維後，每一維上的樣本方差都很大。

     比如下圖有5個樣本點：（已經做過預處理，均值為0，特徵方差歸一）

下面將樣本投影到某一維上，這裡用一條過原點的直線表示（前處理的過程實質是將原點移到樣本點的中心點）。

     假設我們選擇兩條不同的直線做投影，那麼左右兩條中哪個好呢？根據我們之前的方差最大化理論，左邊的好，因為投影后的樣本點之間方差最大。

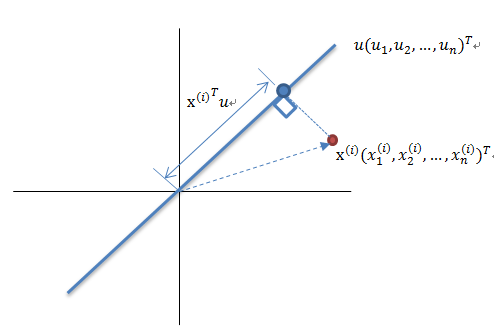
     這裡先解釋一下投影的概念：

     紅色點表示樣例，藍色點表示在u上的投影，u是直線的斜率也是直線的方向向量，而且是單位向量。藍色點是在u上的投影點，離原點的距離是（即或者）由於這些樣本點（樣例）的每一維特徵均值都為0，因此投影到u上的樣本點（只有一個到原點的距離值）的均值仍然是0。

     回到上面左右圖中的左圖，我們要求的是最佳的u，使得投影后的樣本點方差最大。

由於投影后均值為0，因此方差為：

     中間那部分很熟悉啊，不就是樣本特徵的協方差矩陣麼（的均值為0，一般協方差矩陣都除以m-1，這裡用m）。協方差矩陣的介紹在文章後面有講。

     用來表示，表示，那麼上式寫作

     由於u是單位向量，即，上式兩邊都左乘u得，

     即

     We got it！就是的特徵值，u是特徵向量。最佳的投影直線是特徵值最大時對應的特徵向量，其次是第二大對應的特徵向量，依次類推。

因此，我們只需要對協方差矩陣進行特徵值分解，得到的前k大特徵值對應的特徵向量就是最佳的k維新特徵，而且這k維新特徵是正交的。得到前k個u以後，樣例通過以下變換可以得到新的樣本。

     其中的第j維就是在上的投影。

     通過選取最大的k個u，使得方差較小的特徵（如噪聲）被丟棄。

  關於協方差矩陣運算看這裡 

今天看論文的時候又看到了協方差矩陣這個破東西，以前看模式分類的時候就特困擾，沒想到現在還是搞不清楚，索性開始查協方差矩陣的資料，惡補之後決定馬上記錄下來，嘿嘿~本文我將用自認為循序漸進的方式談談協方差矩陣。

統計學的基本概念

學過概率統計的孩子都知道，統計裡最基本的概念就是樣本的均值，方差，或者再加個標準差。首先我們給你一個含有n個樣本的集合，依次給出這些概念的公式描述，這些高中學過數學的孩子都應該知道吧，一帶而過。

均值：


標準差：


方差：
 

很 顯然，均值描述的是樣本集合的中間點，它告訴我們的資訊是很有限的，而標準差給我們描述的則是樣本集合的各個樣本點到均值的距離之平均。以這兩個集合為 例，[0，8，12，20]和[8，9，11，12]，兩個集合的均值都是10，但顯然兩個集合差別是很大的，計算兩者的標準差，前者是8.3，後者是 1.8，顯然後者較為集中，故其標準差小一些，標準差描述的就是這種“散佈度”。之所以除以n-1而不是除以n，是因為這樣能使我們以較小的樣本集更好的 逼近總體的標準差，即統計上所謂的“無偏估計”。而方差則僅僅是標準差的平方。

為什麼需要協方差？

上 面幾個統計量看似已經描述的差不多了，但我們應該注意到，標準差和方差一般是用來描述一維資料的，但現實生活我們常常遇到含有多維資料的資料集，最簡單的 大家上學時免不了要統計多個學科的考試成績。面對這樣的資料集，我們當然可以按照每一維獨立的計算其方差，但是通常我們還想了解更多，比如，一個男孩子的 猥瑣程度跟他受女孩子歡迎程度是否存在一些聯絡啊，嘿嘿~協方差就是這樣一種用來度量兩個隨機變數關係的統計量，我們可以仿照方差的定義：

來度量各個維度偏離其均值的程度，標準差可以這麼來定義：

協方差的結果有什麼意義呢？如果結果為正值，則說明兩者是正相關的(從協方差可以引出“相關係數”的定義)，也就是說一個人越猥瑣就越受女孩子歡迎，嘿嘿，那必須的~結果為負值就說明負相關的，越猥瑣女孩子越討厭，可能嗎？如果為0，也是就是統計上說的“相互獨立”。

從協方差的定義上我們也可以看出一些顯而易見的性質，如：

協方差多了就是協方差矩陣

上一節提到的猥瑣和受歡迎的問題是典型二維問題，而協方差也只能處理二維問題，那維數多了自然就需要計算

多個協方差，比如n維的資料集就需要計算個協方差，那自然而然的我們會想到使用矩陣來組織這些資料。給出協方差矩陣的定義：

這個定義還是很容易理解的，我們可以舉一個簡單的三維的例子，假設資料集有三個維度，則協方差矩陣為

可見，協方差矩陣是一個對稱的矩陣，而且對角線是各個維度上的方差。

總結

1

理解協方差矩陣的關鍵就在於牢記它計算的是不同維度之間的協方差，而不是不同樣本之間，拿到一個樣本矩陣，我們最先要明確的就是一行是一個樣本還是一個維度，心中明確這個整個計算過程就會順流而下，這麼一來就不會迷茫了~