SVM學習——求解二次規劃問題

阿新 • • 發佈：2019-02-13

上一篇最後提到要解決最優化問題： $min_{(w,b)}<w,w>$

$s.t. y_i(<w,x_i>+b) \geq 1$

稍微對它做一下改動，如下：

$min{ \limits_{(w,b)}}\frac{1}{2}||w||^2$

$s.t.$ $y_i(<w,x_i>+b) \geq 1$ $(i=1,2,...n)$

這是一個約束優化問題，更進一步說是一個二次規劃問題，複習一下約束優化問題：

定義1：約束非線性問題是，

其中和都是定義在上的實值連續函式，且至少有一個是非線性的(反之為線性約束優化問題)，m是一個正整數，叫做目標函式，

叫做約束函式，如果目標函式是二次函式則叫做二次規劃問題，由同時滿足所有約束方程的點組成的集合叫做可行域，這些點叫可行點。

定義2:Farkas引理，對於給定的n維向量 $a_i$ $(i=1,2,...m)$ 與b，對於任意滿足 $a_i^TP \geq 0$ $i=1,2...m$ 的向量P，必有 $P^Tb \geq 0$ 的充要條件是：b在向量 $a_i$ $(i=1,2,...m)$ 所形成的凸錐內，即成立： $b=\sum\limits_{i=1}^m{\lambda_ia_i}$ ， $\lambda \geq 0$ $(i=1,2,...m)$ 。

怎麼理解“某個向量在若干其它向量形成的凸錐內”這個描述呢？可以看下圖，

利用平行四邊形法則，可以看到向量b處於由 $a_i$ 形成的凸多邊形內，發揮一下想象力，在空間中這不就像是一個凸的錐狀體嘛。

定義3：對於約束問題，如果有一個可行點 $x^*$ ，存在且滿足

$_8_M`_`A)`B(12%{$%`W32A$

這裡 $c_i(x)$ 都是有效約束。

則 $x^*$ 叫做K-T點。

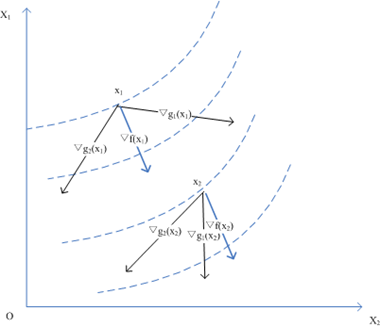
K-T點的幾何意義可以從下圖看出：

顯然x1是K-T點而x2則不是。在一般非線性規劃中，K-T條件是最優解的必要條件但不是它的充分條件，此時K-T點不一定是最優點，但對於凸規劃問題，K-T條件是最優解的充要條件；順便說下，凸規劃是個好同志，它的區域性最優解就是全域性最優解，所以它的K-T點就是全域性最優點。

定理1:設 $x^*$ 是約束問題的區域性極小點， $x^*$ 點處的線性化可行方向的集合等於其序列可行化方向的集合，則必存在 $\lambda^*_i$ $(i=1,2,...n)$ 使得：

這裡 $c_i(x)$ 都是有效約束。

“ $x^*$ 點處的線性化可行方向的集合等於其序列可行化方向的集合”這個條件怎麼滿足呢？只要所有有效約束都是線性函式即可，此時 $x^*$ 必是一個K-T點。

定理2:一階最優性條件：對於可行點 $x^*$ ，如果目標函式和所有有效約束在 $x^*$ 處可微，且任意、非零的，在 $x^*$ 處的序列可行化方向向量d滿足： $3F]U}OD)V8RK1AA4]_[{AKL$ ，則 $x^*$ 為嚴格區域性極小點。這意味著，當向某一點處的任意方向移動都將導致目標函式值上升，那麼這個點不就是一個區域性極小點嘛。

定理3:二階最優性條件：設 $x^*$ 為K-T點， $\lambda^*$ 是相應的拉格朗日乘子，如果，其中d為非零的、 $x^*$ 處的線性化零約束方向，則 $x^*$ 為嚴格的區域性極小點。

推論1：設 $x^*$ 為K-T點， $\lambda^*$ 是相應的拉格朗日乘子，如果對一切滿足的非零向量d都有，則 $x^*$ 為嚴格的區域性極小點。

對於前面的約束非線性規劃問題，如果 $f(x)$ 是二次函式且所有約束是線性函式的時候就變成了二次規劃問題，這一寫成以下形式：

定理4：如果 $x^*$ 是二次規劃問題的可行點，則 $x^*$ 是區域性極小點的充要條件是：當且僅當存在拉格朗日乘子 $\lambda^*$ ，使得：

$g+Hx^*=\sum\limits_{i=1}^{m}{\lambda_i^*a_i}$

$\lambda^*_i[a_i^Tx^*-b_i]=0,$ $i=m_e+1,...m$

$\lambda^*_i \geq 0$ ， $i=m_e+1,...m$

成立，（即 $x^*$ 是K-T點）且對於一切滿足

（其中E為等式的有效約束，I( $x^*$ )為不等式的有效約束）

的向量d都有： $d^THd>0$ 。

定理5:設H為半正定矩陣(所有特徵值大於等於0)，則 $x^*$ 二次規劃問題的全域性極小點當且僅當它是一個區域性極小點或者K-T點。

當H為半正定矩陣，目標函式為凸函式時，該二次規劃被叫做凸二次規劃，它的任何K-T點都是極小點。回想我們開篇要解決的那個問題，目標函式顯然是一個凸函式，所以它是一個凸二次規劃問題，所以一定存在全域性極小點(真好！)。

到此，我們就可以開始解決開篇的那個問題：

$min{ \limits_{(w,b)}}\frac{1}{2}||w||^2$

$s.t.$ $y_i(<w,x_i>+b) \geq 1$

已經確定它是一個凸二次規劃問題了，那麼可以利用其拉格朗日函式： $L(w,b,\alph)=\frac{1}{2}||w||^2-\sum\limits_{i=1}^n\alph_i(y_i(<w,x_i>+b)-1)$

通過對 $w$ 和 $b$ 求偏導數後得到：

$w=\sum\limits_{i=1}^{n}{\alph_iy_ix_i}$

$\sum\limits_{i=1}^{n}{\alph_iy_i}=0$

帶入原始拉格朗日函式，轉化為對偶問題：

$L(w,b,\alph)=\frac{1}{2}||w||^2-\sum\limits_{i=1}^n\alph_i(y_i(<w,x_i>+b)-1)$

$=\frac{1}{2}(\sum\limits_{i,j=1}^n{y_iy_j\alph_i\alph_j<x_i,x_j>})-(\sum\limits_{i,j=1}^n{y_iy_j\alph_i\alph_j<x_i,x_j>})+(\sum\limits_{i=1}^n{\alph_i})$

$=\sum\limits_{i=1}^n{\alph_i}-\frac{1}{2}(\sum\limits_{i,j=1}^n{y_iy_j\alph_i\alph_j<x_i,x_j>})$

這樣就把帶不等式約束的優化問題通過其對偶形式轉化為只帶等式約束的優化問題，即下面的最優化問題W：？？？？

$max \quad\quad\quad\quad W(\alph)=\sum\limits_{i=1}^{n}{\alph_i}-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alph_i\alph_j<x_i,x_j>}$

$s.t.\quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alph_iy_i}=0$

$\alph_i \geq 0 \quad\quad\quad\quad i=1...n$

求得 $\alph_i$ 後就得到了 $w^*=\sum\limits_{i=1}^{n}\alph_i^*y_ix_i$ ，它使得幾何間隔 $\gamma=\frac{1}{||w||}$ 取最大值，從而得到最優分類超平面。

K-T點要滿足的條件還有一個是： $\alph^*_i(y_i(<w^*_i,x_i>+b^*)-1) =0$ ，這個式子說明了什麼問題呢？

1、顯然，函式間隔不等於1的那些輸入點的拉格朗日系數必為0(這些點是非積極因素)，而函式間隔恰好為1的輸入點的拉格朗日系數則不為0(這些點是積極因素)，這說明確定最終分類超平面的就是這些函式間隔為1的邊界點，所以這些輸入點就是支援向量(Support Vector)。從這裡也能看出支援向量機的抗干擾能力比較強，對非積極因素的擾動對於最優化解沒有影響；

2、 $y_i(<w^*,x_i>+b^*)-1=0$ ，其中i為支援向量，因為： $y(<w^*,x_i>+b^*)=y(\sum\limits_{i \in support \quad vector}y_i\alph_i^*<x_i,x>+b^*)=1$

，我們的目標函式 $<w^*,w^*>=\sum\limits_{i,j \in support \quad vector}{y_iy_j\alph_i^*\alph_j^*<x_i,x_j>$

$=\sum\limits_{j \in support \quad vector}{\alph_j^*y_j}\sum\limits_{i \in support \quad vector}{y_i\alph_i^*<x_i,x_j>}$

$=\sum\limits_{j \in support \quad vector}{\alph_j^*y_j}(\frac {1} {y_j}-b^*)$

$=\sum\limits_{i \in support \quad vector}{\alph^*_i}$ (注意這裡 $b^*$ 為常數，且有約束條件 $s.t.\quad\quad\quad\quad \sum\limits_{i=1}^{n}{\alph_iy_i}=0$ ）

於是通過這樣的對偶轉化，我們得到了實現幾何間隔為 $\gamma=\frac{1}{||w^*||}={(\sum\limits_{i \in support \quad vector}\alph^*_i)}^{1/2}$ 的最大間隔超平面。

通過上面的推導也可以看出將二次規劃轉化為其對偶問題可以簡化約束條件，讓我們記住最優化問題W吧，這是一個很牛逼的轉化，這個式子還有個特點，就是“資料僅出現在內積中”。

前面的討論都是說輸入樣本是線性可分的時候怎麼找到最大間隔超平面來劃分兩類資料，那麼如果輸入樣本是線性不可分的，那可怎麼辦呀，前面的那些討論不就成徒勞的了麼？學習SVM後才知道它牛的地方，如果我們可以通過某種函式對映將輸入樣本對映到另外一個高維空間並使其線性可分的話，前面的討論結果不就都可以用到了麼，還記得“資料僅出現在內積中”吧，假設這個對映關係是： $\Phi:X->F$ ，這時候的內積 $<x_i,x_j>$ 就變成了 $<\Phi(x_i),\Phi(x_j)>$ ，如果有方法能夠將內積 $<\Phi(x_i),\Phi(x_j)>$ 直接算出，就將把輸入樣本“從低維空間向高維空間對映”和“求對映後的內積”這兩步合併成了一步，這樣直接計算的方法就是核函式方法，下篇學習核函式吧，SVM的理論部分還是很數學的啊！

SVM學習——求解二次規劃問題

SVM學習——求解二次規劃問題

python求解二次規劃問題

MatLab建模學習筆記9——二次規劃問題求解

二次規劃——學習筆記

matlab二次規劃求解

學習 MeteoInfo二次開發教程（一）

學習 MeteoInfo二次開發教程（三）

學習 MeteoInfo二次開發教程（四）

學習MeteoInfo二次開發教程（十二）

等式約束的二次規劃問題

用於復變動力二次規劃的復值張神經網路總結

無約束演算法-最速下降，牛頓法，擬牛頓，共軛梯度求解二次函式極小值

二次規劃（quadratic programming）

求解二次同餘式

Mtlab 二次規劃及其例子

[求解二次剩餘數論技巧隨機化] Ural 1132 Square Root

約束規劃問題與凸二次規劃

Matlab學習手記——二次多項式曲面擬合

[斐波那契數列求解二次剩餘&二次模方程 BSGS] COGS 2114 [CodeChef FN]斐波那契數

Java基礎知識二次學習--第八章流

SVM學習——求解二次規劃問題

相關推薦