座標旋轉變換公式的推導
翻譯自: http://www.metro-hs.ac.jp/rs/sinohara/zahyou_rot/zahyou_rotate.htm
翻譯: 湯 永康
出處: http://blog.csdn.NET/tangyongkang
轉貼請註明出處
1 圍繞原點的旋轉
如下圖, 在2維座標上,有一點p(x, y) , 直線opの長度為r, 直線op和x軸的正向的夾角為a。 直線op圍繞原點做逆時針方向b度的旋轉,到達p’ (s,t)
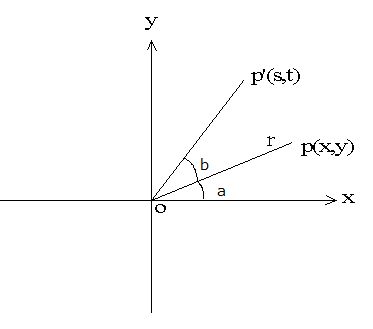
s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b) (1.1)
t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b) (1.2)
其中 x = r cos(a) , y = r sin(a)
代入(1.1), (1.2) ,
s = x cos(b) – y sin(b) (1.3)
t = x sin(b) + y cos(b) (1.4)
用行列式表達如下:
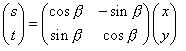
2.座標系的旋轉
在原座標系xoy中, 繞原點沿逆時針方向旋轉theta度, 變成座標系 sot。
設有某點p,在原座標系中的座標為 (x, y), 旋轉後的新座標為(s, t)。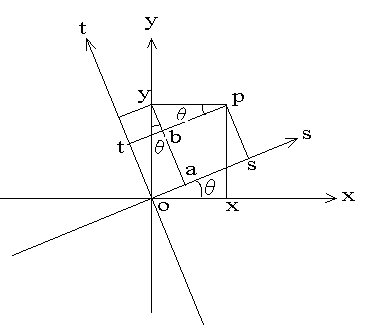
oa = y sin(theta) (2.1)
as = x cos(theta) (2.2)
綜合(2.1),(2.2) 2式
s = os = oa + as = x cos(theta) + y sin(theta)
t = ot = ay – ab = y cos(theta) – x sin(theta)
用行列式表達如下:
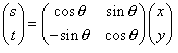
相關推薦
座標旋轉變換公式的推導
翻譯自: http://www.metro-hs.ac.jp/rs/sinohara/zahyou_rot/zahyou_rotate.htm 翻譯: 湯 永康 出處: http://blog.csdn.NET/tangyongkang 轉貼請註明出處 1 圍繞原點的旋轉 如下圖, 在2維座標上,有一點p
平面內直角座標系中座標旋轉變換公式
首先上公式: 逆時針(如下圖): x1=xcos(β)-ysin(β); y1=ycos(β)+xsin(β); 順時針(圖未給出): x1=xcos(β)+ysin(β); y1=
已知任意平面方程,推導座標旋轉變換的結論與方法(進階篇),願願原創。
作為本部落格《已知任意平面方程,推導座標旋轉變換的結論與方法,願願原創。》(連結:https://blog.csdn.net/tom_xuzg/article/details/83034006)的姊妹篇,本文將繼續探討,座標旋轉變換,不同之處,上一篇用了三次旋轉變換,這一篇要用兩次旋轉變換。上一篇結
已知任意平面方程,推導座標旋轉變換的結論與方法(終極篇),願願原創。
本文將繼續探討,座標旋轉變換,不同之處,上兩篇各用三次,兩次旋轉變換,這一篇要用一次旋轉變換。 如下圖: 如圖,還是任意的平面方程,o2-xy面,在該平面上,如棕色和草綠色箭頭所示,我們的目標是,經過一次選擇,達到我們的o2-x‘’y‘’z‘’與o2-xyz重合的目的(也就是,棕色軸與
座標旋轉變換的角度正方向。願願原創。
第一種方法: 判斷一個旋轉變換的角度是正還是負,首先,要確定該進行變換的座標系是左手系還是右手系。拇指對準x軸正方向,食指對
三維座標旋轉轉換公式(JavaScript)
此方法以右手座標系為準 function rotate_z(x, y, z, angle) { var atopi = angle / 180 * Math.PI; var xtoz = x * Math.cos(ato
影象旋轉變換的推導
前面我們提到了影象的縮放變換,可以用矩陣乘法的形式來表達變換後的畫素位置對映關係。 那麼,對於旋轉變換呢?我們可以同樣將其想象成二維平面上向量的旋轉。如下圖所示,向量[x1,y1]逆時針旋轉θθ度到了[x2,y2]。 設定向量的長度為s,根據座標系定義
旋轉矩陣公式推導
1.在二維平面中:如下圖所示,在xoy 平面中有一向量op⃗=(x,y) T ,旋轉ϕ 角後變為向量op⃗ ′ =(x ′ ,y ′ ) T 。 據圖可得:x=|op⃗|c
傅立葉變換概念及公式推導
傅立葉變換(FT) 傅立葉變換的目的是可將時域(即時間域)上的訊號轉變為頻域(即頻率域)上的訊號,隨著域的不同,對同一個事物的瞭解角度也就隨之改變,因此在時域中某些不好處理的地方,在頻域就可以較為簡單的處理。 傅立葉變換公式:
三角形重心座標公式推導
定理:已知三角形△A1A2A3的頂點座標Ai ( xi , yi ) ( i =1, 2, 3) 。則它的重心座標為: xg = (x1+x2+x3) / 3 ; yg = (y1+y2+y3) / 3 ; 設三點為A(x1.y1)B(x2
單應性(homography)變換的公式推導過程
原文地址:http://www.cnblogs.com/ml-cv/p/5871052.html 矩陣的一個重要作用是將空間中的點變換到另一個空間中。這個作用在國內的《線性代數》教學中基本沒有介紹。要能形像地理解這一作用,比較直觀的方法就是影象變換,影象變換
POJ 2140 Herd Sums 公式推導
cpp true typedef 因數 固定 ostream highlight ring sum 題意:給出n<=1e7 求有多少個連續數之和等於k x+x+1+....x+k=n (k+1)k/2+(k+1)x=n (k+1)k+(k+1)2x=2*n (k
vijos - P1543極值問題(斐波那契數列 + 公式推導 + python)
找到 span add gin python3 abi pri n) fill P1543極值問題 Accepted 標簽:[顯示標簽] 背景 小銘的數學之旅2。 描寫敘述 已知m、n為整數,且滿足下列兩個條件: ①
vijos - P1302連續自然數和 (公式推導 + python)
.net ble tags ucid stat down bsp z-index fontsize P1302連續自然數和 Accepted 標簽:[顯示標簽] 描寫敘述 對一個給定的自然數M,求出所有的連續的自然數段(連續個數大於1)
解釋一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推導過程(轉載)
線性不可分 itl 專註 out center forest 測試 重要 原因 KPCA,中文名稱”核主成分分析“,是對PCA算法的非線性擴展,言外之意,PCA是線性的,其對於非線性數據往往顯得無能為力,例如,不同人之間的人臉圖像,肯定存在非線性關系,自己做的基於ORL數據
繞任意軸旋轉的矩陣推導總結
format spl 基礎 imp 平行四邊形 mage 方法 關系 建立 前言 常用的幾何變換中旋轉是較為復雜的一種,最近看《Physically Based Rendering, Second Edition: From Theory To Implementation
SVM公式推導筆記
svm width org sin .org 參考資料 zhang www http 參考資料: 對偶函數-http://blog.pluskid.org/?p=702 KTT和拉格朗日乘子-http://www.cnblogs.com/zhangchaoyan
反向傳播算法(過程及公式推導)
不能 簡化 會有 geo 之前 代碼 求和 不同 eof 一、反向傳播的由來 在我們開始DL的研究之前,需要把ANN—人工神經元網絡以及bp算法做一個簡單解釋。關於ANN的結構,我不再多說,網上有大量的學習資料,主要就是搞清一些名詞:輸入層/輸入神經元,輸出層/輸出神經元,
機器學習之支持向量機(一):支持向量機的公式推導
根據 監督式 art 通用 利用 哪些 這就是 在線 方法 註:關於支持向量機系列文章是借鑒大神的神作,加以自己的理解寫成的;若對原作者有損請告知,我會及時處理。轉載請標明來源。 序: 我在支持向量機系列中主要講支持向量機的公式推導,第一部分講到推出拉格朗日對偶函數的對偶因
最速降線問題公式推導
關系 工作 第一個 int sub dash calc quad 證明 以前對物理特別感興趣的時候就專門研究過一段時間的變分法,記得當時閱讀了一本十分不錯的書籍,其作者名挺有趣的—老大中先生的《變分法基礎》(真的很不錯的一本講變分法的書,有興趣的同學可以去看
