以測量的角度:從中心極限定理到假設檢驗
阿新 • • 發佈:2019-05-14
近來讀一篇Paper,研究者利用假設檢驗來驗證兩個不同消費者是否一起逛商場。
同時最近在看 G.H.韋恩堡的《數理統計初級教程》,藉著這個機會,所以把假設檢驗梳理歸納了一下,從測量的角度。個人統計測量水平有限,錯漏之處,若有大神指點,不勝感激。
一切的基礎,高斯分佈
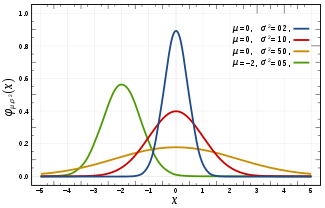
所有知道數理統計的人,恐怕沒有不知道高斯分佈(正態分佈)的,所以這裡直接引維基的介紹:
大部分的統計問題,測量問題,包括像最小二乘的平差,都是建立在正態分佈的基礎上。對於很多非高斯分佈, 也有通過某種轉化變成到高斯分佈來分析。
中心極限定理
維基的解釋為:
中心極限定理是概率論中的一組定理。中心極限定理說明,在適當的條件下,大量相互獨立隨機變數的均值經適當標準化後依分佈收斂於正態分佈。這組定理是數理統計學和誤差分析的理論基礎,指出了大量隨機變數之和近似服從正態分佈的條件。
但《數理統計初級教程》的說法恐怕更好懂:
假定等容量的隨機樣本都從同一無限總體取樣,則每一個樣本的和構成的新分佈漸進正態分佈。(而且!! 原總體分佈不一定要是正態分佈)
同理根據正態分佈的特性,把該定義拓展到對於每個樣本的均值構成的新分佈,也是漸進正態分佈的。 而且該新分佈的均值與原總體的均值相同,而該新分佈的標準差與原總體的標準差之比為根號N.
一個尺子測量的例子
問題的提出: 如果有一把尺子,用來測量一段距離,大部分人都知道,多測幾次取均值是可取的。如果有粗差知識(outlier),可能會進行粗差剔除後取均值。類似於裁判打分去掉最高分,去掉一個最低分。 那麼這個取均值的背後,事實上是基於觀測資料僅含有偶然誤差,也就是說尺子本身沒有系統誤差的情況下的最優估計。那麼如何判斷一把尺子到底有沒有系統誤差呢? 自然而然,我們會想到需要一個基準(或者說一個真實值已知的距離,這裡叫他基線)然後通過測量該值來對尺子進行檢驗。具體一點,假如有一根基線長為100cm, 利用一把尺子測量了該基線多次,結果為99,100,101, 101,測量均值u=100.3,那麼這個0.3到底是偶然誤差(也就說這個尺子可以認為沒系統誤差,可以拿去測量其他的東西),還是具有系統誤差(需要糾偏,比如說每個測量值都減去0.3)呢? 直觀上,0.3/100很小,尺子應該沒誤差吧。 但是,直覺對科學很重要,僅靠直覺不去量化驗證又是不科學的。 那麼統計學的做法是什麼呢? 首先,光靠100.3這個值我們其實很難保證說這個尺子就一定沒問題,因為你不能通過舉正例來證明你的觀點。但是話說回來,如果利用反證法,也就說我們假如能夠證明沒誤差的尺子測出來100.3的概率非常小,那麼這個尺子幾乎是一定有問題,需要再校正的。這其實就是假設檢驗最基礎的intuition. 而這個intuition放在正態分佈裡面,反例是什麼確定的呢? 反例就是那些只有極小概率才會發生的值,對應到正態分佈概率密度鍾型曲線靠近兩邊的那些取值。 也就是說,假如你告訴我說你這個x~N(100,1),然後我取一個觀測值x,結果這個x竟然是很小概率(p<5%)才會發生的值,那麼我就不得不懷疑你這個假設的正確性了。對應到尺子的例子,那就是這個正態分佈的準確性了(基線長度)或者就得懷疑這個觀測值x的取值方法(尺子有系統誤差)是不是正確了!!!也就是否認你這個x~N(100, 1)的假設了! 這是因為正態分佈的特徵主要由期望和方差決定: 1. 這個均值分佈的總體期望我們知道,假如方差也知道,那麼分佈就完全確定了 3. 所以在這個均值方差都知道的分佈裡,我們可以計算某個概率區間的上下限(比如說可以知道落在X1-X2的概率是95%)。 4. 那麼如果一個樣本在X1-X2中,那麼我們沒理由認為這個尺子有問題(雖然它還是可能有問題,但是我們無法判斷它 只能接受它沒問題)。而如果落在那5%的區間裡(x<X1或者x>X2),我們認為你在逗我吧這麼小的概率你也搞到,那肯定是你自己有問題(尺子有系統誤差),也就是拒絕接受尺子沒問題這個設定,你回去再校正吧。 再舉個例子:你假設你手上的硬幣是均勻的,然後你投擲了100次,結果發現90次都是正面,那你敢相信這個假設是對的嗎?所以這也牽涉出來,假設檢驗的目的,在於否定原假設,原假設否定不了我們才接受備選假設。注意是接受了假設,而不是證明了假設。什麼意思呢,比如100次投擲裡50次正面,符合我們的假設,但是依然沒人敢保證這個假設是嚴格正確的,只能說從統計資料來看沒辦法證明它是錯的,那就暫時認為它是對的吧。 在這個intuition明白之後,假設檢驗的流程也明白了: 1. 確定原假設H0(比如尺子沒問題,硬幣均勻), 和備選假設H1(尺子有問題,硬幣不均勻) 2. 確定我們在什麼時候會拒絕原假設,通常是0.05 也就是說假如統計資料竟然落在那5%裡面,我要拒絕原假設 3. 在原假設的基礎上去探尋該統計資料可能出現的概率,看齊是否小於5% 那麼這個intuition如何拓展開呢? 1. 假設可能不是直接針對於分佈本身 (統計量的選取,字樣的函式,其分佈應該已知比如t分佈) 2. 如果抽樣的資料本身不是正態分佈呢? ---> 中心極限定理 3. 如果主體的方差和期望並不已知的情況下如何判斷概率呢? 這個時候就是利用t-分佈這個統計量了:值得注意的是,當子樣容量n>=200 用樣本方差代替總體方差被認為是嚴密的,>30時候認為用樣本方差代替總體方差進行檢驗的結果可信(u檢驗和t檢驗一致)。 中心極限定理: 為什麼我們假設尺子沒問題的話多測測量的均值滿足正態分佈? 首先,這把尺子測量的4次結果,相當於統計中的從總體中(無數把尺子對該基線進行測量的資料總體)抽出來來的一個樣本,不難想象,假如總體樣本有無限把尺子進行測量,就算尺子本身有系統誤差也會有不同的系統誤差相互抵消,也就是說總體的期望值為100, 這就是中心極限定理:從大容量的同一總體中抽取等容量的樣本,則每一個樣本的均值構成的分佈趨近於正態分佈且期望為總體的期望。 寫到這裡突然覺得,還是先看《數理統計初級教程》第十,第十一章後,細看《誤差理論與測量平差基礎》第十一章來的清楚,作罷作罷。參考:
&n