論文標題：Support Vector Method for Novelty Detection

論文作者：Bernhard Scholkopf, Robert Williamson, Alex Smola .....

論文地址：http://papers.nips.cc/paper/1723-support-vector-method-for-novelty-detection.pdf

宣告：小編翻譯論文僅為學習，如有侵權請聯絡小編刪除博文，謝謝！

            小編是一個機器學習初學者，打算認真學習論文，但是英文水平有限，所以論文翻譯中用到了Google，並自己逐句檢查過，但還是會有顯得晦澀的地方，如有語法/專業名詞翻譯錯誤，還請見諒，並歡迎及時指出。

摘要

　　假設給你一個從基本概率分佈P中提取的資料集，你想估計一個輸入空間的“簡單”子集，這樣從 P中提取的測試點位於S 之外的概率等於和之間指定的某個先驗概率。我們提出了一種方法來解決這個問題，嘗試估計一個函式 f ，它在S上是正的，在補語上是負的。f的函式形式是根據訓練資料的一個潛在的小子集通過核展開給出的；它是通過控制相關特徵空間中權重向量的長度來正則化的。我們對演算法的統計效能進行了理論分析。該演算法是支援向量演算法對未標記資料的自然擴充套件。

1，介紹

　　近年來，一套新的監督學習核心技術被開發出來[8]。特別是用於模式識別，迴歸估計和反問題求解的支援向量（SV）演算法受到了廣泛的關注。有幾次嘗試將利用核函式計算特徵空間內積的思想轉移到無監督學習領域。然而，該領域中的問題沒有那麼明確。一般來說，他們可以被描述為資料的估計函式，這些函式告訴您關於底層分佈的一些有趣的資訊。例如，核主成分分析可以被描述為對訓練資料產生單位方差輸出而在特徵空間具有最小范數的計算函式[4]。另一種基於核的無監督學習技術，正則化主流形[6]，其計算函式可以對映到低維流行上，從而最大程度地減少了正則化量化誤差。聚類演算法是可以被核心化的無監督學習技術的進一步示例。

　　一個極端的觀點是，無監督學習是關於估計密度的，顯然，對於P的密度的瞭解將使我們能夠解決根據資料可以解決的任何問題，本工作解決了一個更簡單的問題：提出了一種演算法，該演算法計算一個二進位制函式，該函式應捕獲概率密度存在的輸入空間中的區域（它的支援），即使大多數資料都位於該區域中的函式 函式為非零[5]。這樣做，是符合瓦普尼克（Vapnik）的原則，永遠不解決比我們實際需要解決的問題更普遍的問題。此外，它也適用於資料分佈密度甚至沒有很好定義的情況，例如，如果存在奇異成分，本研究的主要動機是論文[1]，事實證明，之前的工作量很大。

2，演算法

　　我們首先介紹術語和符號慣例，我們考慮訓練資料 x1, x2....xl 屬於 X ，其中 l 屬於N 是觀測的數量，X是一些集合。為了簡單起見，我們將其設為 R^N 

的一個緊湊子集。設 Φ 是 X ->  F 的特性對映，即到點積空間F中的對映，使得Φ 的影象點積可以通過評估一些簡單的核來計算

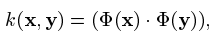
 　　例如高斯核：

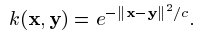
 　　索引 i 和 j 被認為在 i,....,j  的範圍內（簡寫為：i, j 屬於 [l]）粗體的希臘字母表示 l-維向量，其分量用普通字型標註。

　　在本節的其餘部分中，我們將開發一種演算法，該演算法返回一個函式F，該函式在捕獲大部分資料點的“小”區域中取值 +1，而在其他地方則取值 -1。我們的策略是將資料對映到與核心相對應的特徵空間中，並以最大的餘量將他們與原點分開。對於新點 x，值f(x) 是通過評估特徵空間上落在超平面的哪一側來確定。通過自由利用不同型別的核函式，此簡單的幾何影象對應於輸入空間中的各種非線性估計。

　　該問題的優化目標與二分類 SVM 略微不同，但依然很相似。

 　　為了將資料集與原點分離，我們求解一下二次規劃：

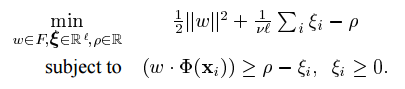
 　　此處，v屬於(0, 1) 是一個引數，其含義稍後將變得清楚。由於非零鬆弛變數 ξi 在目標函式中受到懲罰，我們可以預期，如果 w 和 p解決了這個問題，則對於訓練集中包含的大多數示例 xi ，決策函式 f(x) = sgn((w*Φ(x))-p) 將會為正，而SV型別正則項 W 仍然很小。這兩個目標之間的實際權衡由 v 控制的。匯出對偶問題，並使用（1），可以證明該解決方案具有 SV 展開。

　　注意，這裡的 v 類似於二分類 SVM 中的C，同時：

• 1， v 為異常值的分數設定了一個上限（訓練資料集裡面被認為是異常的）
• 2， v 是訓練資料集裡面做為支援向量的樣例數量的下屆 

　　因為這個引數的重要性，這種方法也被稱為  v-SVM 。採用 Lagrange技術並且採用 dotproduct calculation，確定函式如下：

 　　具有非零 i 的模式 Xi 稱為SV，其中找到係數作為對偶問題的解：

　　可以使用標註QP例程解決此問題。然而，它確實擁有一些特性，使其與一般 qp 不同，最顯著的時約束的簡單性。可以通過應用為此目的開發的 SMO 變體加以利用[3]。

　　偏移量p可以通過利用對於不在上限或下限的任何 αi 的對應模式 xi 滿足 ρ = (w*Φ(x))=。。。

　　注意，如果 v 接近，Lagrange 乘子的上界區域無窮大，即（6）中的第二個不等式約束變為無效。從原始目標函式（3）可以看出，由於錯誤的懲罰變得無限，因此，這個問題類似於相應的硬邊界演算法，可以證明如果資料集與原點可分離，則該演算法將找到具有唯一屬性的支援超平面，並且在所有此類超平面中，距原點的距離最大[3]。另一方面，如果 v 接近1，則僅約束允許一個解，即所有 i 都在上限 1/(vl) 處。在這種情況下，對於具有整數1 的核心，例如（2）的規範化版本，決策函式對應於閾值 Parzen 視窗估計器。

　　作為本節的總結，我們注意到，人們還可以使用球來描述特徵空間的資料，其實質與【2】的演算法（具有硬邊界）和【7】的演算法（具有軟邊界）密切相關。對於某些類的核，例如高斯RBF核，可以顯示出相應的演算法與上面的演算法是等價的【3】。

3，理論

　　在這一節中，我們證明了引數表徵了SVs和離群值的分數（命題1）。然後，我們給出了軟邊值（命題2）和誤差界（命題5）的魯棒性結果。進一步的結果和證明已在本論文中的全文中報告【3】。我們將使用斜體字母表示輸入空間中對應模式的特徵空間圖形，即 xi: = Φ(Xi)。

命題1 假設（4）的解滿足 p!=0，以下陳述成立：

（1）是離群值部分的上限

（2）是SVs分數的下限

（3）假設資料是獨立與不包含離群分量的分佈 P(x) 生成的。此外，假設核心是分析性的並且是非恆定的。漸進的，概率為1，等於SV的分數和異常值的分數。

　　證明基於對偶問題的約數，適用了離群值必須在上限處具有拉格朗日乘數的事實。

命題2 與W平行的離群值的區域性運動不會改變超平面。

 我們現在繼續討論一般化的問題。我們的目標是將從相同的基本分佈中提取新點位於估計區域之外的概率限制在一定的範圍內。我們首先介紹一個通用工具，用於測量對映X到R的F類函式的容量。

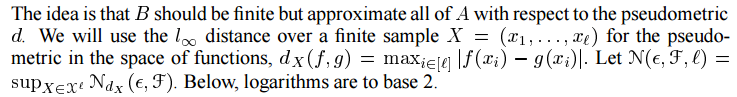
命題3 設（X，d）為偽度量空間，令A為X的子集且epsilon>0。如果每個a屬於A，都存在b屬於B，使得d(a, b)<=epsilon，A的 epsilon-conver Nd(epsilon, A) 是A的epsilon-cover 的最小基數（如果沒有這樣的有限覆蓋，則定義為無窮大）

 　　這個想法是B應該是有限的，但相對於偽度量 d 近似於A的全部。我們將在有限空間樣本 X=(X1...Xl) 上的 L無窮 距離用於函式空間中的偽度量。   下面的對數以2為底。

 命題4 考慮到任何P在X的分佈，和任何 rho 屬於R，假設x1,....xl 是來自P的i.i.d，然而，如果我們發現 f屬於F使得對於所有的 f(xi) = -theta + rho

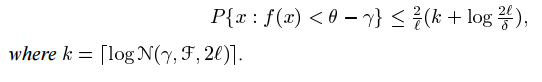
 　　我們現在考慮對於少數點 f(xi)不能超過 a+b 的可能性，這相當於在演算法中具有一個非零的鬆弛變數 epsilon i ，在定理的應用中，我們取  gama + theta=rho/||W|| 並使用特徵空間中的線性函式類，覆蓋此類的日誌有眾所周知的界限。令f 為空間 X 上的實值函式。在theta 屬於R，x 屬於 X，定義

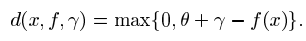
 　　類似的，對於一個訓練序列 X，我們定義

 命題5 令 theta=R，考慮一個固定但未知的概率分佈P在輸入空間 X 和範圍為[a,  b]的一類實數函式F。然後 對於所有的隨機繪製的在大小為 l 的訓練序列 x，對於所有的  tho>0 並且任何的 f 屬於 F，有：

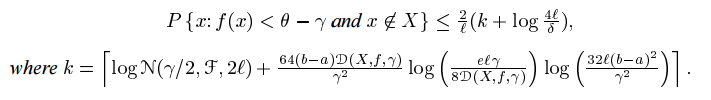
 　　該定理限制了一個新點落入 f(x)的值小於 rho-gamma，這是對分配支援的估計的補充。對的選擇在邊界所保持的區域的大小（r增加，區域的大小）與它所保持的概率的大小（r 增加，對數覆蓋數的大小）之間進行權衡。

　　結果表明，我們可以用涉及對數覆蓋數之比（可以由與 r 成比例的脂肪破碎位數來界定）與訓練次數之比的數量來限制點落在估計支援範圍之外的概率。示例，再加上涉及鬆弛變數1範數的因子。它比【1】給出的相關結果更強，因為他們的邊界涉及Pollard維數（r趨於0時的脂肪破碎位數）與訓練樣本數之比的平凡根。

 　　輸出的演算法描述在Sec.2，是一個函式 f(x) 在示例 xi上大於或等於i。儘管在輸入控制元件中是非線性的，但是這函式實際上在核心k 定義的特徵空間中是線性的。同時，權向量的2範數的許可權向量是B給出的。因此我們可以將定理應用到函式類F為空間特徵中以B為邊界的2範數的那些線性函式。如果我們假設 theta是已知的，然後 gamma=rho-theta，因此分佈的集合是支援集合的。並且根據函式類別F的對數覆蓋範圍和鬆弛變數 ξi 的總和，邊界給出了隨機生成的點落在該集合之外的可能性，由於F級的對數覆蓋數可以由 O限制，因此就權重向量的2範數給出了一個限制。由於日誌覆蓋數在 類F 的 gamma/2 可以在 O 給出的範圍內，這給出了權向量的2範數的界。

 　　理想情況下，人們希望在確定 theta 的值後選擇 tho，也許將其作為該值的固定分數。這可以通過在某個可能值的 rho 或至少一個網格的可能值上將結果風險最小化的另一個級別來實現。該結果超出了當前初步論文的範圍，但是結果的形式類似於定理5，具有更大的常數和對數因子。

　　雖然給出具體的理論建議以供實際使用尚未過早，但從上述界限可以清楚地看出一件事。為了歸納為異常的資料，要使用的決策函式應該採用 閾值 eta*rho，其中 eta<1（ rho 對應一個非零值）

4，實驗

 　　我們將該方法應用於人工資料和真實資料，圖1展示了二維玩具示例，並顯示了引數設定如何影響解決方案。

　　接下來，我們描述了對於 USPS 手寫數字資料集的實驗。該資料庫包含大小Wie 16*16=256 的9298 位數字影象；最後的2007年構成測試集。我們在測試集上使用寬度 c = 0.5*256（該資料集上SVM分類器的通用值，參見【2】）的高斯核訓練了該演算法，並用它來識別離群值——是社群中的民間傳說，由於分割錯誤或標籤錯誤，USPS測試集包含許多難以分類或無法分類的模式。在實驗中，我們將輸入模式增加了十個與數字的類別標籤相對應的維度。這樣做的理由是，如果我們忽略標籤，就沒有希望將錯誤標籤的模式識別為異常值。圖2顯示了USPS測試集的20個最差離群值。注意，該演算法確實提取出很難分配給他們各自類別的模式。在實驗中，在以 450 MHz 執行的 Pentium || 上花費了幾秒鐘，我們使用了 5% 的 v 值。

 　　圖1，前兩張圖片，適用於兩個玩具問題的單類SVM；v=c=0.5，域：[-1, 1]²，請注意，在這兩種情況下，所有示例中至少 v 的一小部分如何位於估計區域中（參見表）。v的較大的值導致左上角的其他資料點對決策功能幾乎沒有影響。對於較小的v值，例如 0.1（第三張圖片），這些點將不再被忽略。或者，可以通過更改核心寬度（2）來強制演算法將這些“離群值”考慮在內：在第四張圖片中，使用 c=0.1，v=0.5 可以在不同的長度範圍內有效的分析資料，這導致演算法考慮了離群值是有意義的點。

 　　圖2：由提出的演算法識別的離群值，按SVM的負輸出（決策函式中 sgn的自變數）排名。輸出（為了方便起見，以 10**-5為單位）以斜體寫在每個影象的下方，（對應的 ）類標籤以粗體顯示。請注意，大多數示例都是“困難”的，因為他們不是典型的，甚至標記錯誤的。

 5，討論

　　可以將當前的工作視為提供一種符合 Vapnik 原理的演算法的嘗試，該演算法永遠不會解決比實際感興趣的問題更籠統的問題。例如，在僅對檢測感興趣的情況下 異常，並不一定總是需要顧及資料的完整密度模型。的確，在幾個方面，密度估算比我們所做的更加困難。

 　　從數學上講，僅當基礎概率測度具有絕對連續的分佈函式時，密度才會存在。估計大類集合的度量的一般問題（例如，以Borel的意義衡量的集合）是無法解決的（有關討論，請參見【8】）。因此，我們需要限制自己對某些集合的度量進行陳述。給定一類集合，完成此任務的最簡單估計器是經驗測度，它只是檢視有多少訓練點落入感興趣區域。我們的演算法則相反，它從應該落入該區域的的訓練點數量開始，然後估計具有所需熟悉的區域。通常，會有很多這樣的區域解方案通過應該正則化器才能變得唯一，在我們的情況下，這強制了該區域在與核心關聯的特徵空間中較小。當然，這意味著，在這種意義上，較小程度的度量取決於所使用的核心，其方式與在特徵空間中進行正則化的任何其他方式沒有什麼不同。但是，在輸入空間中進行密度估計時，已經出現了類似的問題。令 P 表示 X 上的密度。如果我們在輸入域 X 中執行（非線性）座標變換，則密度值將發生變化；粗略地說，保持不變的是 px*dx，而 dx 也進行了轉換。當直接估計區域的概率度量時，我們不會遇到這個問題，因為區域會相應的自動更改。

 　　我們選擇使用的小度量的一個吸引人的屬性是，它也可以在正則化理論的上下文中，從而導致該解在某種程度上取決於所使用的特定核心而被解釋為最大平滑【3】

 　　我們的方法的主要靈感來自 Vapnik和合作者的早期工作。他們提出了一種演算法，該演算法通過使用超平面將其與原點分離來表徵一組未標記的資料點【9】。但是，無論從演算法還是從那時開始的統計學習理論的理論發展來看，他們都迅速轉向了兩類分類問題。從演算法的角度來看，我們可以找出原始方法的兩個缺點，這些缺點可能導致該放下的研究停止了三十多年。首先，原始演算法僅限於輸入空間中的線性決策規則，其次，無法處理離群值，結合起來，這些限制確實很嚴格-通用資料集不需要通過輸入空間中的超平面與原點分離。我們合併的兩個修改消除了這些缺點。首先，核心技巧通過非線性對映到高維特徵空間中提供了更大的功能類別，從而增加了與原點分離的機會。特別是，使用高斯核（2），對於任何資料集 x1....xl  都存在這樣的分類，x：要看清楚這一點，請注意，對於所有的 K(Xi,  Xj) >0，因此所有點積均為正，暗示所有對映的模式都在同一個 orthant內。此外，由於所有的 i 的 k(Xi,  Xj)=1 因此他們具有單位長度。因此他們與原點是可分離的。第二張修改允許出現異常值的可能性。我們使用  trick 結合了決策規則的“軟性”，因此可以直接處理異常值。

 　　我們認為我們的方法提出了一種具有良好計算複雜度的具體演算法（凸二次規劃），以解決迄今為止主要從理論角度進行研究的問題，具有廣泛的實際應用。為了使該演算法稱為從業人員易於使用的黑盒方法，必須解決諸如選擇核心引數（例如高斯核心的寬度）之類的問題，我們期望我們在本文中簡要概述的理論將為這一艱鉅的任務提供基礎。

 致謝   這項工作的一部分是由ARC和DFG（＃Ja379 / 9-1）支援的，而BS是在澳大利亞國立大學和GMD FIRST期間完成的。 AS由Deutsche Forschungsgemeinschaft（Sm 62 / 1-1）資助。 感謝S.Ben David，C。Bishop，C。Schnörr和M. Tipping的有益討論。

相關推薦