如果需要處理的原圖及程式碼，請移步小編的GitHub地址

　　傳送門：請點選我

　　如果點選有誤：https://github.com/LeBron-Jian/ComputerVisionPractice

1，如何提高影象畫素

　　對曝光過度或者逆光拍攝的圖片可以通過直方圖均衡化的方法用來增強區域性或者整體的對比度。

　　對於相機採集的原始影象經常會出現一種現象，即影象所有畫素的灰度值分佈不均勻，而是集中在某一特定的小區域，導致影象中的所有資訊的灰度值都很接近，即對比度差，很難從影象中分辨出某一特徵的資訊。而質量較高的影象中，畫素的強度應該均衡的分佈。

　　為了提高影象處理的效果，經常會在影象處理之前進行直方圖均衡化，即將影象的直方圖灰度級別由集中在某一小部分灰度級分散成在所有灰度級別都有一定的覆蓋，所以通過直方圖均衡化的方法用來增強區域性或整體的對比度。

　　具體的思路就是通過找出影象中最亮和最暗的畫素值將之對映到純黑和純白之後再將其他的畫素值按照某種演算法對映到純黑和純白之間的值。另外一種方法就是尋找影象中畫素的平均值作為中間灰度值，然後擴充套件範圍以達到儘量充滿可顯示的值。

　　一個好的影象會有來自影象的所有區域的畫素。所以你需要把這個直方圖拉伸到兩端(如上圖所給出的)，這就是直方圖均衡的作用(用簡單的話說)。這通常會改善影象的對比度。

2，直方圖均衡化的原理

2.1  直方圖的介紹

　　具體直方圖實現的原理是什麼呢？請看下圖：

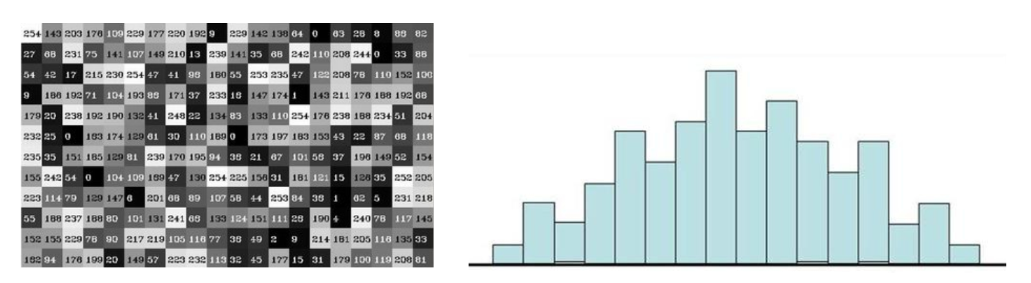
 　　左圖是一個影象的畫素組合，我們拿到的是一個12*20 大小的影象畫素；右圖就是他的直方圖展示，橫軸表示在0~255之間的區間塊，我們將其分為16個bin，統計影象中每個畫素的個數，右圖反映的時影象中每個畫素出現的頻率，橫軸是畫素區間，縱座標是畫素出現的頻率。

　　看到上面兩個圖，大概直方圖的解釋應該很明顯了。

2.2  用實驗資料展示什麼是直方圖？

　　我們可以把直方圖看做一個圖，它給我們一個關於影象的強度分佈的總體思路。它是一個帶有畫素值的圖（從0到255， 不總是）在X軸上，在y軸上的影象對應的畫素個數。

　　這只是理解影象的另一種方式，通過觀察影象的直方圖，我們可以直觀的瞭解影象的對比度，亮度，亮度分佈等。（下圖來至於Cambridge in Color website的圖片，建議去訪問這個網站，瞭解更多細節。）

　　你可以看到影象和它的直方圖。（這個直方圖是用灰度影象繪製的，而不是彩色影象）。在直方圖中，橫座標表示影象中各個畫素點的灰度級，縱座標表示具有該灰度級的畫素個數。直方圖的左邊部分顯示了影象中較暗畫素的數量，右邊區域顯示了更明亮的畫素。從直方圖中可以看到，深色區域的畫素數量比亮色區域更多，而中間色調的數量(中值大約在127左右)則少得多。

2.3 直方圖均衡化的原理

　　有時影象的視覺上的缺陷並不在強度值集中在很窄的範圍內。而是某些強度值的使用頻率很大。在完美均衡的直方圖中，每個柱的值都應該相等。即50%的畫素值應該小於128,25%的畫素值應該小於64.總結出的經驗可定義為：在標準的直方圖中 p% 的畫素擁有的強度值一定小於或等於 255*p%，將該規律用於均衡直方圖中：強度 i 的灰度值應該在對應的畫素強度低於 i 的百分比的強度中。因此，所需要的查詢表可由下面的式子建立：

lut[i] = int(255.0 *p[i]) #p[i]是是強度值小於或等於i的畫素的數目。

　　p[i] 即直方圖累計值，這是包含小於給點強度值的畫素的直方圖，以代替包含指定強度值畫素的數目。比如第一幅影象的累計直方圖如下圖中的藍線：

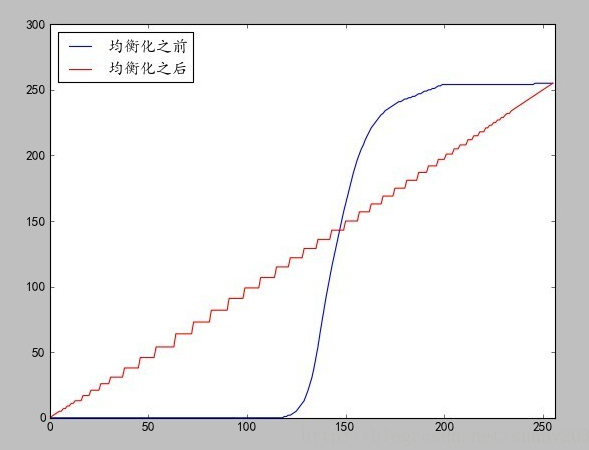
 　　而完美均衡的直方圖，其累積直方圖應為一條斜線，如上圖中均衡化之後的紅線。

　　更專業一點，這種累計直方圖應該稱為累計分佈（cumulative  distribition）。在Numpy中有一個專門的函式來計算。這個在後面說。

　　所以直方圖均衡化就是對影象使用一種特殊的查詢表。通常來說，直方圖均衡化大大增加了影象的表象。但是根據影象可視內容的不同，不同影象的直方圖均衡化產生的效果不盡相同。下面我們具體學習一下。

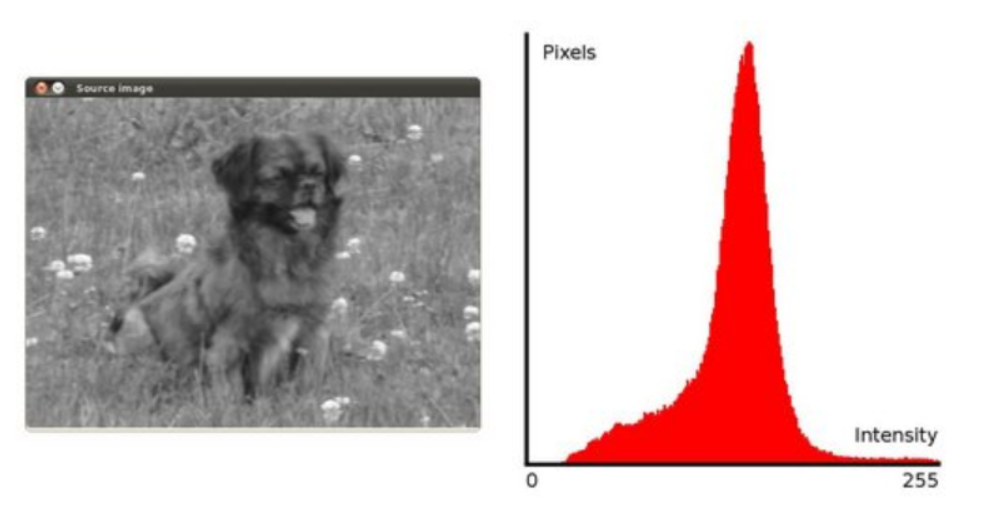
　　比如下圖小狗，我們畫出原圖，並展示出其畫素直方圖分佈範圍：

 　　我們對直方圖進行均衡化，均衡化的圖，如下：

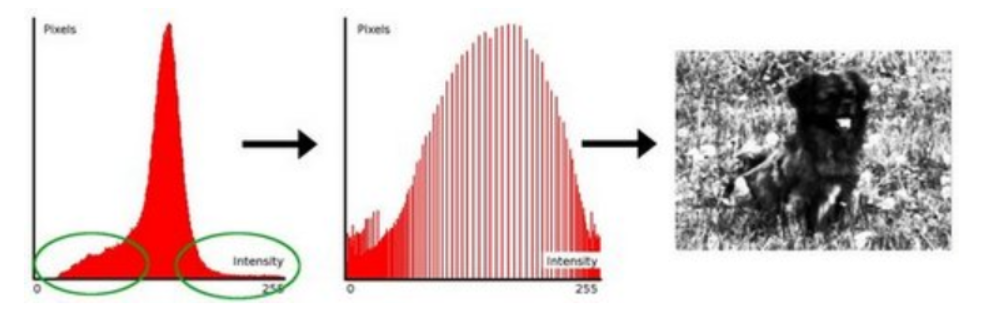
 　　最終我們得到了小狗直方圖均衡化後的影象。那其計算原理如下圖：

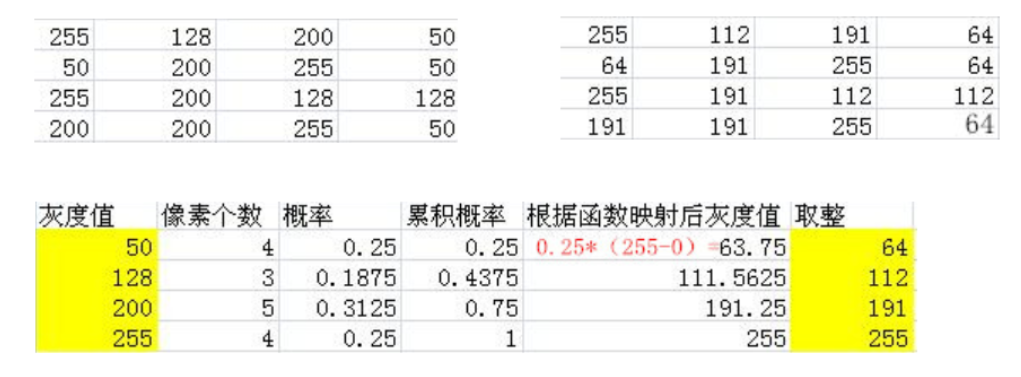
 　　簡單解釋一下，上面兩張圖是我們取了圖片中一點畫素，是我們直方圖均衡化前後的兩張表的對比。那麼如何進行直方圖均衡化的計算，也就是將左圖的畫素點轉換為右圖呢，我們就需要下圖的計算過程了。圖很明顯，我就不再贅述了。

　　下面首先對直方圖的計算進行學習，然後學習直方圖均衡化。

3，直方圖的繪製

3.1  使用OpenCV統計繪製直方圖

　　OpenCV提供了cv.calcHist()函式來獲取直方圖，與C++中一樣，都是cv.calcHist()。讓我們熟悉一下這個函式及其引數：

def calcHist(images, channels, mask, histSize, ranges, hist=None, accumulate=None): 
    # real signature unknown; restored from __doc__
    """
    calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]]) -> hist
    .   @overload
    """
    pass

• images：它是uint8型別或float32的源影象。當傳入函式時，它要用方括號括起來，也就是”[img]”。
• channels：它也用方括號括起來。它是我們計算直方圖的通道的索引。例如，如果輸入是灰度影象，它的值是0。對於顏色影象，您可以通過0、1或2來分別計算藍色、綠色或紅色通道的直方圖，即BGR通道。
• mask：遮罩圖。為了找到完整影象的直方圖，它被指定為“None”。但如果你想找到影象的特定區域的直方圖，你必須為它建立一個遮罩圖，並將其作為遮罩。
• histSize：這代表了我們的BINS數。需要用方括號來表示。在整個範圍內，我們通過了256。
• ranges：強度值範圍，通常是 [ 0，256 ]

　　讓我們從一個樣本影象開始，只需要在灰度模式下載入影象並找出其完整的直方圖：

#_*_coding:utf-8_*_
import cv2  # opencv讀取的格式是BGR
import numpy as np
import matplotlib.pyplot as plt  # Matplotlib讀取的格式是RGB

img = cv2.imread('cat.jpg', 0)   #0 表示灰度圖
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
print(hist.shape)  #  (256, 1)

　　hist是一個256x1陣列，每個值對應於該影象中的畫素值機器對應的畫素值。

3.2  使用Numpy計算直方圖

　　Numpy中提供了np.histogram()方法，用於對一位陣列進行直方圖統計，其引數列表入下：

Histogram(a,bins=10,range=None,normed=False,weights=None)

• a：是儲存待統計的陣列
• bins：指定統計的區間個數，即對統計範圍的等分數
• range：是一個長度為2的元組，表示統計範圍的最大值和最小值，預設值為None，表示範圍由資料的範圍決定，即(a.min(), a.max))。
• normed：當normed引數為False時，函式返回陣列a中的資料在每個區間的個數，否則對個數進行正規化處理，使它等於每個區間的概率密度。
• weights：weights引數和 bincount()的類似

返回值（有兩個）

• hist : hist和之前計算的一樣，每個區間的統計結果。
• bins : 陣列，儲存每個統計區間的起點。range為[0,256]時，bins有257個元素，因為Numpy計算bins是以0-0.99,1-1.99等，所以最後一個是255-255.99。為了表示這一點，他們還在bins的末端添加了256。但我們不需要256。到255就足夠了。

　　讓我們從一個樣本影象開始。只需在灰度模式下載入影象並找到其完整的直方圖

hist, bins = np.histogram(img.ravel(), 255, [0,256])

　　Numpy還有另一個函式，np.bincount()，比np.histograme()要快得多(大約10X)。對於一維直方圖，你可以試一下。不要忘記在np.bincount中設定minlength=256。例如，hist=np.bincount(img.ravel()，minlength=256)

　　OpenCV函式比np.histogram()快（大約40X）。所以考慮效率的時候堅持用OpenCV函式。

3.3   使用matplotlib繪製直方圖

　　Matplotlib中有一個繪製直方圖的函式：

matplotlib.pyplot.hist()

　　引數：資料來源必須是一維陣列，通常要通過函式 ravel() 拉直影象，畫素一般是256，表示[0, 256]。

　　函式ravel() 將多維陣列降為一維，格式為：一維陣列 =  多維陣列.ravel()

　　hist()直接找到直方圖繪製。您不需要使用calcHist()或np.histogram()函式來找到直方圖。看下面的程式碼：

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('cat.jpg', 0)
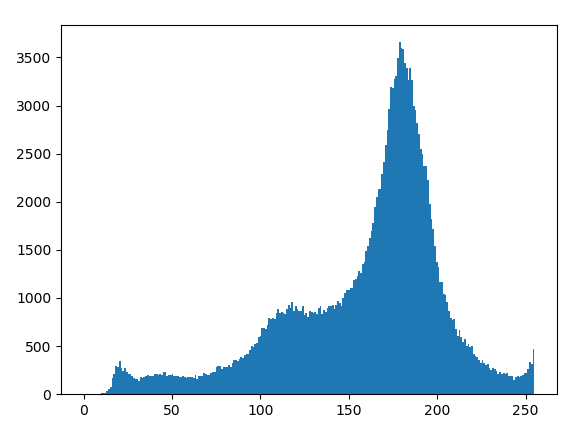
plt.hist(img.ravel(), 256, [0,256])
plt.show()

　　效果如下：

　　或者我們可以用常規的matplotlib的plot函式繪製直方圖，適合繪製BGR影象直方圖。為此，我們需要首先找到直方圖的資料，程式碼如下：

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('cat.jpg')
color = ('b', 'g', 'r')
for i, col in enumerate(color):
    histr = cv.calcHist([img], [i], None, [256], [0,256])
    plt.plot(histr, color=col)
    plt.xlim([0,256])
plt.show()

　　效果如下：

4   彩色影象不同通道的直方圖

　　下面來看下彩色影象的直方圖處理，首先讀取並分離各通道，接著計算每個通道的直方圖，這裡將其封裝成函式，接著呼叫，程式碼如下：

import cv2
import numpy as np


def calcAndDrawHist(image, color):
    hist = cv2.calcHist([image], [0], None, [256], [0.0, 255.0])
    minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc(hist)
    histImg = np.zeros([256, 256, 3], np.uint8)
    hpt = int(0.9*256)

    for h in range(256):
        intensity = int(hist[h] * hpt / maxVal)
        cv2.line(histImg, (h, 256), (h, 256-intensity), color)

    return histImg

def show_histphoto(photo_path):
    image = cv2.imread(photo_path)
    b, g, r = cv2.split(image)

    histImgB = calcAndDrawHist(b, [255, 0, 0])
    histImgG = calcAndDrawHist(b, [0, 255, 0])
    histImgR = calcAndDrawHist(b, [0, 0, 255])

    cv2.imshow('histImgB', histImgB)
    cv2.imshow('histImgG', histImgG)
    cv2.imshow('histImgR', histImgR)
    cv2.imshow('Img', image)
    cv2.waitKey(0)
    cv2.destroyAllWindows()


if __name__ == '__main__':
    photo_path = 'cat.jpg'
    show_histphoto(photo_path)

　　三個通道的直方圖如下：

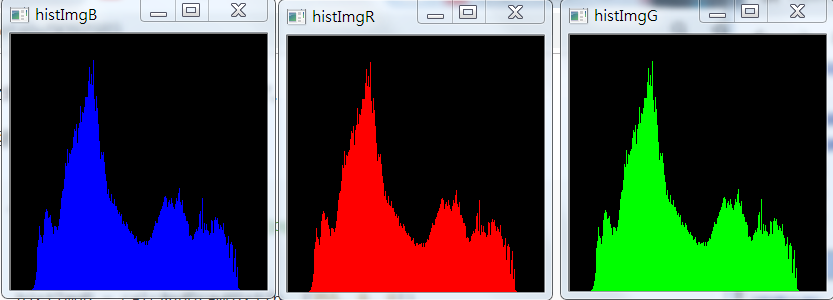
　　圖如下：

4.1  更進一步

　　這樣做有些繁瑣，參考（https://plus.google.com/118298613334549762938）的做法，無需分離通道，用折現來描繪直方圖的邊界可在一副圖中同時繪製三個通道的直方圖。方法如下：

def Line_chart(photo_path):
    image = cv2.imread(photo_path)
    # 建立用於繪製直方圖的全0 影象
    h = np.zeros((256, 256, 3))
    # 直方圖中各bin的頂點位置
    bins = np.arange(256).reshape(256, 1)
    # BGR 三種顏色
    color = [(255, 0, 0), (0, 255, 0), (0, 0, 255)]
    for ch, col in enumerate(color):
        originHist = cv2.calcHist([image], [ch], None, [256], [0, 256])
        cv2.normalize(originHist, originHist, 0, 255*0.9, cv2.NORM_MINMAX)
        hist = np.int32(np.around(originHist))
        pts = np.column_stack((bins, hist))
        cv2.polylines(h, [pts], False, col)

    h = np.flipud(h)
    cv2.imshow('colorhist', h)
    cv2.waitKey(0)

if __name__ == '__main__':
    photo_path = 'cat.jpg'
    # show_histphoto(photo_path)
    Line_chart(photo_path)

　　結果如下：

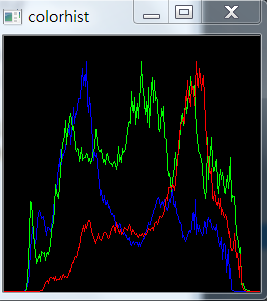
程式碼說明：

　　這裡的for迴圈是對三個通道遍歷一次，每次繪製相應通道的直方圖的折線。for迴圈的第一行是計算對應通道的直方圖，經過上面的介紹，應該很容易就能明白。

　　這裡所不同的是沒有手動的計算直方圖的最大值再乘以一個係數，而是直接呼叫了OpenCV的歸一化函式。該函式將直方圖的範圍限定在0-255×0.9之間，與之前的一樣。下面的hist= np.int32(np.around(originHist))先將生成的原始直方圖中的每個元素四捨六入五湊偶取整（cv2.calcHist函式得到的是float32型別的陣列），接著將整數部分轉成np.int32型別。即61.123先轉成61.0，再轉成61。注意，這裡必須使用np.int32(...)進行轉換，numpy的轉換函式可以對陣列中的每個元素都進行轉換，而Python的int(...)只能轉換一個元素，如果使用int(...)，將導致only length-1 arrays can be converted to Python scalars錯誤。

　　下面的pts = np.column_stack((bins,hist))是將直方圖中每個bin的值轉成相應的座標。比如hist[0] =3，...，hist[126] = 178，...，hist[255] = 5；而bins的值為[[0],[1],[2]...,[255]]。使用np.column_stack將其組合成[0, 3]、[126, 178]、[255, 5]這樣的座標作為元素組成的陣列。

　　最後使用cv2.polylines函式根據這些點繪製出折線，第三個False引數指出這個折線不需要閉合。第四個引數指定了折線的顏色。

　　當所有完成後，別忘了用h = np.flipud(h)反轉繪製好的直方圖，因為繪製時，[0,0]在影象的左上角。這在直方圖視覺化一節中有說明。

5，直方圖均衡化

5.1   使用OpenCV繪製直方圖均衡化

　　我們可以調整直方圖的值和它的bin值，讓它看起來像x，y座標，這樣你就可以用cv.line()或cv.polyline()函式來繪製它，從而生成與上面相同的影象。這已經是OpenCV-Python2官方的樣本了。檢視sampl/python/hist.py的程式碼。我們用cv.calcHist()函式來找一張完整的圖片的直方圖。但是我們只要圖片的一部分的直方圖呢？在你想要找到的區域中，建立一個帶有白色的遮罩影象。然後把它作為遮罩

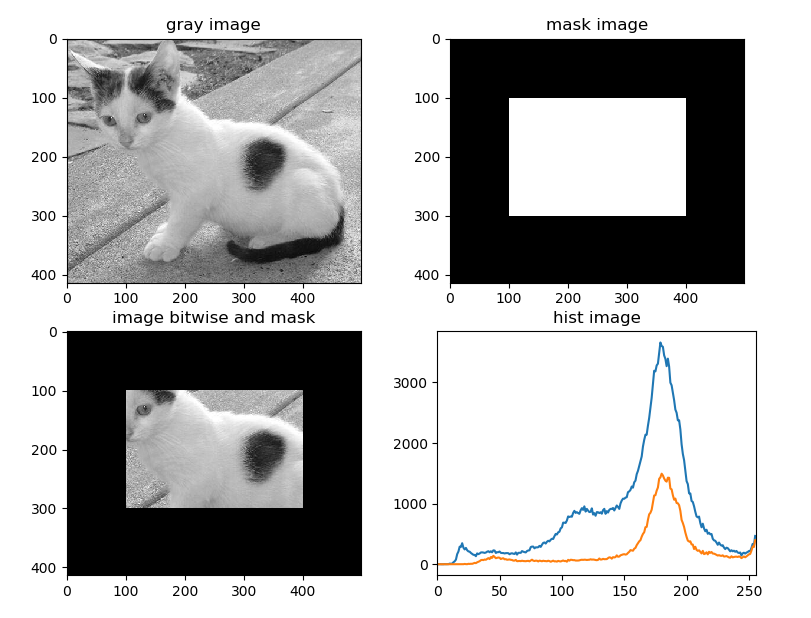
　　我們可以拿到一幅影象進行mask操作，並且可以看一下其直方圖分佈：

#_*_coding:utf-8_*_
import cv2  # opencv讀取的格式是BGR
import numpy as np
import matplotlib.pyplot as plt  # Matplotlib讀取的格式是RGB

img = cv2.imread('cat.jpg', 0)

# 建立 mask
mask = np.zeros(img.shape[:2], np.uint8)
print(mask.shape)  # (414, 500)
mask[100:300, 100:400] = 255

masked_img = cv2.bitwise_and(img, img, mask=mask)  # 與操作

hist_full = cv2.calcHist([img], [0], None, [256], [0, 256])
hist_mask = cv2.calcHist([img], [0], mask, [256], [0, 256])

plt.subplot(221), plt.imshow(img, 'gray'), plt.title('gray image')
plt.subplot(222), plt.imshow(mask, 'gray'), plt.title('mask image')
plt.subplot(223), plt.imshow(masked_img, 'gray'), plt.title('image bitwise and mask')
plt.subplot(224), plt.plot(hist_full), plt.plot(hist_mask), plt.title('hist image')
plt.xlim([0, 256])
plt.show()

　　效果如下：

　　OpenCV有一個函式可以這樣做，cv.equalizeHist()，它封裝好了計算cdf和cdf重對映以及根據cdf表生成直方圖均衡影象的過程。它的輸入只是灰度影象，輸出是我們的直方圖均衡影象。

img = cv.imread('cat,jpg', 0)
equ = cv.equalizeHist(img)
res = np.hstack((img, equ)) # 並排疊加圖片
cv.imwrite('res.png', res)

　　所以現在你可以用不同的光條件來拍攝不同的影象，平衡它，並檢查結果。

　　當影象的直方圖被限制在一個特定的區域時，直方圖均衡是很好的。在那些有很大強度變化的地方，直方圖覆蓋了一個大區域，比如明亮的和暗的畫素，這樣的地方就不好用了。

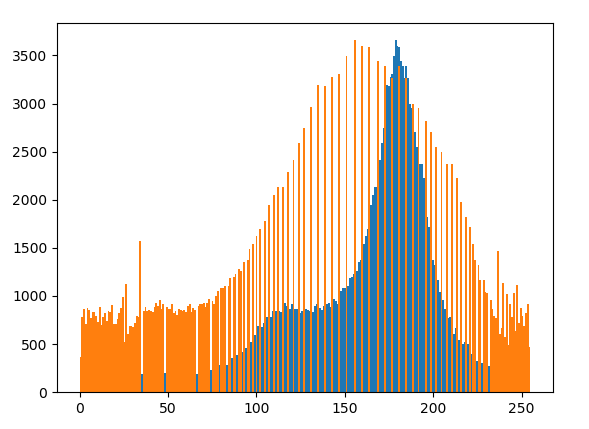
　　我們可以看看直方圖均衡化之前和之後的直方圖分佈圖。

　　補充程式碼如下：

plt.hist(img.ravel(), 256)
plt.hist(equ.ravel(), 256)
plt.show()

 　　展示在一個直方圖，效果如下：

5.2   使用OpenCV繪製自適應直方圖均衡化

 　　區域性直方圖均衡化，即把影象分成許多小塊（比如按 8*8 作為一個小塊），那麼對每個小塊進行均衡化。這種方法主要對影象直方圖不是那麼單一的（比如存在多峰情況）的影象比較實用。

　　直方圖自適應直方圖均衡化的原始碼如下：

def createCLAHE(clipLimit=None, tileGridSize=None): # real signature unknown; restored from __doc__
    """
    createCLAHE([, clipLimit[, tileGridSize]]) -> retval
    .   @brief Creates a smart pointer to a cv::CLAHE class and initializes it.
    .   
    .   @param clipLimit Threshold for contrast limiting.
    .   @param tileGridSize Size of grid for histogram equalization. Input image will be divided into
    .   equally sized rectangular tiles. tileGridSize defines the number of tiles in row and column.
    """
    pass

　　引數說明：

• clipLimit：顏色對比度的閾值
• titleGridSize：進行畫素均衡化的網格大小，即在多少網格下進行直方圖的均衡化操作

　　程式碼如下：

#_*_coding:utf-8_*_
import cv2  # opencv讀取的格式是BGR
import numpy as np
import matplotlib.pyplot as plt  # Matplotlib讀取的格式是RGB

img = cv2.imread('cat.jpg', 0)

equ = cv2.equalizeHist(img)
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))

res_clahe = clahe.apply(img)


res = np.hstack((img, equ, res_clahe)) 
cv2.imshow('res', res)
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　效果如下：

　　示例1：單通道的灰階圖的直方圖均衡化

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt


im = cv.imread("test.png", 0)
cv.imshow("before", im)

# Histogram Equalization
im2 = cv.equalizeHist(im)
print(im2)

cv.imshow("after", im2)
plt.show()
cv.waitKey(0)

　　示例2：彩圖的直方圖均衡

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt


im = cv.imread("test.jpg")
cv.imshow("before", im)

# split g,b,r
g = im[:,:,0]
b = im[:,:,1]
r = im[:,:,2]


# Histogram Equalization
r2 = cv.equalizeHist(r)
g2 = cv.equalizeHist(g)
b2 = cv.equalizeHist(b)

im2 = im.copy()
im2[:,:,0] = g2
im2[:,:,1] = b2
im2[:,:,2] = r2

print(im2)

cv.imshow("after", im2)
plt.show()
cv.waitKey(0)

　　示例3：帶遮罩的直方圖均衡化

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt

im = cv.imread("test.png", 0)
cv.imshow("before", im)
mask = cv.imread("test_mask2.png", 0)
cv.imshow("mask", mask)

# calculate histogram with mask
hist_mask = cv.calcHist([im], [0], mask, [256], [0,256])

# calculate cdf with mask
cdf = hist_mask.cumsum()

# Histogram Equalization
cdf = (cdf-cdf[0])*255/(cdf[-1]-1)
cdf = cdf.astype(np.uint8)# Transform from float64 back to unit8

# generate img after Histogram Equalization
im2 = np.zeros((384, 495, 1), dtype =np.uint8)
im2 = cdf[im]

# im2 = cv.equalizeHist(im)
print(im2)

cv.imshow("after", im2)
plt.show()
cv.waitKey(0)

5.2，使用Numpy進行直方圖均衡化

　　計算累積和的 cumsun()函式

numpy.cumsum(a, axis=None, dtype=None, out=None)

　　這個函式的功能是返回給定axis上的累積和

>>>import numpy as np  
>>> b=[1,2,3,4,5,6,7]  
>>> np.cumsum(a)  
array([  1,   3,   6,  10,  15,  21,  28,  36,  45,  55,  75, 105])

　　直方圖均衡化

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('wiki.jpg', 0)

hist, bins = np.histogram(img.flatten(), 256, [0,256])

cdf = hist.cumsum()
cdf_normalized = cdf*float(hist.max())/cdf.max()

plt.plot(cdf_normalized, color = 'b')
plt.hist(img.flatten(),256,[0,256], color = 'r')
plt.xlim([0,256])
plt.legend(('cdf','histogram'), loc = 'upper left')
plt.show()

　　你可以看到直方圖位於更亮的區域。我們需要讓它充滿整個頻譜。為此，我們需要一個轉換函式，它將更亮區域的輸入畫素對映到全區域的輸出畫素。這就是直方圖均衡所做的。

　　現在我們找到了最小的直方圖值(不包括0)，並應用了在wiki頁面中給出的直方圖均衡等式。

cdf = (cdf-cdf[0]) *255/ (cdf[-1]-1)
cdf = cdf.astype(np.uint8)

　　現在我們有了一個查詢表，它提供了關於每個輸入畫素值的輸出畫素值的資訊。所以我們只要應用變換。

img2 = cdf[img]

　　另一個重要的特徵是，即使影象是一個較暗的影象(而不是我們使用的更亮的影象)，在均衡之後，我們將得到幾乎相同的影象。因此，它被用作一種“參考工具”，使所有的影象都具有相同的光照條件。這在很多情況下都很有用。例如，在人臉識別中，在對人臉資料進行訓練之前，人臉的影象是均勻的，使它們具有相同的光照條件。

　　示例1：單通道的灰階圖的直方圖均衡化

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt

img = cv.imread("test.png", 0)
cv.imshow("before", img)

# calculate hist
hist, bins = np.histogram(img, 256)
# calculate cdf
cdf = hist.cumsum()
# plot hist
plt.plot(hist,'r')

# remap cdf to [0,255]
cdf = (cdf-cdf[0])*255/(cdf[-1]-1)
cdf = cdf.astype(np.uint8)# Transform from float64 back to unit8

# generate img after Histogram Equalization
img2 = np.zeros((384, 495, 1), dtype =np.uint8)
img2 = cdf[img]

hist2, bins2 = np.histogram(img2, 256)
cdf2 = hist2.cumsum()
plt.plot(hist2, 'g')

cv.imshow("after", img2)
plt.show()
cv.waitKey(0)

　　我們可以看到，直方圖均衡化後的影象對比度增強了。

　　示例2：彩圖的直方圖均衡化

　　首先是分離通道，對比三個通道分別進行處理，合併三通道顏色到圖片

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt


img = cv.imread("test.png")
cv.imshow("before", img)

# split g,b,r
g = img[:,:,0]
b = img[:,:,1]
r = img[:,:,2]

# calculate hist
hist_r, bins_r = np.histogram(r, 256)
hist_g, bins_g = np.histogram(g, 256)
hist_b, bins_b = np.histogram(b, 256)

# calculate cdf
cdf_r = hist_r.cumsum()
cdf_g = hist_g.cumsum()
cdf_b = hist_b.cumsum()

# remap cdf to [0,255]
cdf_r = (cdf_r-cdf_r[0])*255/(cdf_r[-1]-1)
cdf_r = cdf_r.astype(np.uint8)# Transform from float64 back to unit8
cdf_g = (cdf_g-cdf_g[0])*255/(cdf_g[-1]-1)
cdf_g = cdf_g.astype(np.uint8)# Transform from float64 back to unit8
cdf_b = (cdf_b-cdf_b[0])*255/(cdf_b[-1]-1)
cdf_b = cdf_b.astype(np.uint8)# Transform from float64 back to unit8

# get pixel by cdf table
r2 = cdf_r[r]
g2 = cdf_g[g]
b2 = cdf_b[b]

# merge g,b,r channel
img2 = img.copy()
img2[:,:,0] = g2
img2[:,:,1] = b2
img2[:,:,2] = r2

# show img after histogram equalization
cv.imshow("img2", img2)

cv.waitKey(0)

　　示例三：帶遮罩的直方圖均衡化

　　如果想要在做直方圖均衡化的時候不考慮影象的某一部分，比如我們不想考慮圖片右上角的雲彩，那麼可以使用遮罩在計算hist和cdf時不考慮這一部分畫素。

import cv2 as cv
import numpy as np 
from matplotlib import pyplot as plt


img = cv.imread("test.png", 0)
cv.imshow("src", img)

# load mask img
mask = cv.imread("test_mask2.png", 0)
cv.imshow("mask", mask)

# apply mask to src
masked_img = np.ma.masked_array(img, mask = mask)
masked_img = np.ma.filled(masked_img,0).astype('uint8')
# print(masked_img)
masked_img = np.ma.masked_equal(masked_img,0)
# print(masked_img)
cv.imshow("masked_img", masked_img)


# calculate hist
hist, bins = np.histogram(masked_img.compressed(), 256) # img have to be compressed() to let mask work
# calculate cdf
cdf = hist.cumsum()

print(cdf)
# plot hist
plt.plot(hist,'r')

# remap cdf to [0,255]
cdf = (cdf-cdf[0])*255/(cdf[-1]-1)
cdf = cdf.astype(np.uint8)# Transform from float64 back to unit8

# generate img after Histogram Equalization
img2 = np.zeros((384, 495, 1), dtype =np.uint8)
img2 = cdf[img]

hist2, bins2 = np.histogram(img2, 256)
cdf2 = hist2.cumsum()
plt.plot(hist2, 'g')

cv.imshow("dst", img2)
plt.show()
cv.waitKey(0)

6，使用查詢表（LUT）來拉伸直方圖

　　在影象處理中，直方圖均衡化一般用來均衡影象的強度，或增加影象的對比度。在介紹使用直方圖均衡化來拉伸影象的直方圖之前，先學習使用查詢表的方法。

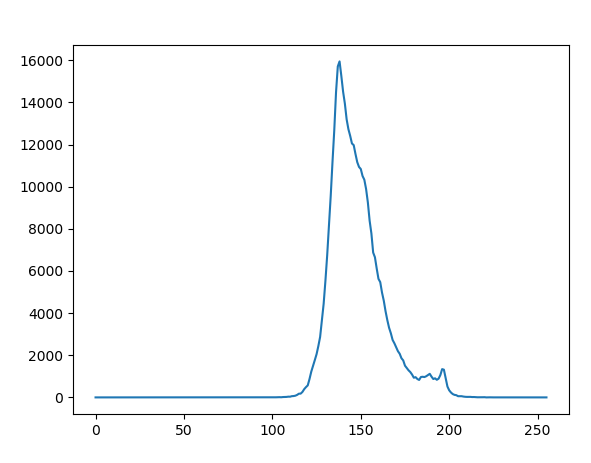
　　直方圖的繪製程式碼如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_histphoto(photo_path):
    image = cv2.imread(photo_path, 0)
    print(image.shape)
    hist = cv2.calcHist([image], [0], None, [256], [0.0, 256.0])
    # print(hist.shape)
    plt.plot(hist)

def Line_chart(photo_path):
    image = cv2.imread(photo_path)
    # 建立用於繪製直方圖的全0 影象
    h = np.zeros((256, 256, 3))
    # 直方圖中各bin的頂點位置
    bins = np.arange(256).reshape(256, 1)
    # BGR 三種顏色
    color = [(255, 0, 0), (0, 255, 0), (0, 0, 255)]
    for ch, col in enumerate(color):
        originHist = cv2.calcHist([image], [ch], None, [256], [0, 256])
        cv2.normalize(originHist, originHist, 0, 255*0.9, cv2.NORM_MINMAX)
        hist = np.int32(np.around(originHist))
        pts = np.column_stack((bins, hist))
        cv2.polylines(h, [pts], False, col)

    h = np.flipud(h)
    cv2.imshow('colorhist', h)
    cv2.waitKey(0)

if __name__ == '__main__':
    photo_path = 'test.jpg'
    # show_histphoto(photo_path)
    Line_chart(photo_path)

　　（一種藉助matplotlib，程式碼簡單，一種使用opencv，需要轉化）

 　　觀察上圖中原始影象的直方圖，很容易發現大部分強度值範圍都沒有用到。因此先檢測影象非0的最低（imin）強度值和最高（imax）強度值。將最低強度值imin設定為0，最高值 imax 設為255。中間的按照255.0*（i - imin）/（imax - imin）+ 0.5)的形式設定。

　　實現的任務主要集中在查詢表的建立中，程式碼如下：

minBinNo, maxBinNo = 0, 255

# 計算從左起第一個不為0的直方圖位置
for binNo, binValue in enumerate(hist):
    if binValue != 0:
        minBinNo = binNo
        break

# 計算從右起第一個不為0的直方圖位置
for binNo, binValue in enumerate(reversed(hist)):
    if binValue != 0:
        maxBinNo = 255 - binNo
        break

# 生成查詢表
for i, v in enumerate(lut):
    if i < minBinNo:
        lut[i] = 0
    elif i > maxBinNo:
        lut[i] = 255
    else:
        lut[i] = int(255.0*(i-minBinNo)/(maxBinNo-minBinNo)+0.5)

　　查詢表建立完成後，就直接呼叫相應的OpenCV函式，這裡呼叫的時 cv2.LUT函式：

#計算
result = cv2.LUT(image, lut)

　　cv2.LUT 函式只有兩個引數，分別為輸入影象和查詢表，其返回處理的結果。

　　完整程式碼如下：

import cv2
import numpy as np

image = cv2.imread('wiki.jpg', 0)
# 建立空的查詢表
lut = np.zeros(256, dtype=image.dtype)
# OpenCV提供了cv.calcHist()函式來獲取直方圖
hist = cv2.calcHist([image],  # 計算影象的直方圖
                    [0],  # 使用的通道
                    None,  # 沒有使用mask
                    [256],  # it is a 2D histogram
                    [0.0, 255.0])
# print(hist.shape)  # (256, 1)
minBinNo, maxBinNo = 0, 255

# 計算從左起第一個不為0的直方圖位置
for binNo, binValue in enumerate(hist):
    if binValue != 0:
        minBinNo = binNo
        break

# 計算從右起第一個不為0的直方圖位置
for binNo, binValue in enumerate(reversed(hist)):
    if binValue != 0:
        maxBinNo = 255 - binNo
        break

# 生成查詢表
for i, v in enumerate(lut):
    if i < minBinNo:
        lut[i] = 0
    elif i > maxBinNo:
        lut[i] = 255
    else:
        lut[i] = int(255.0 * (i - minBinNo) / (maxBinNo - minBinNo) + 0.5)

# 計算
result = cv2.LUT(image, lut)
print(result.shape)   # (534, 800)
cv2.imshow('result', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

　　效果如下：

7，直方圖均衡化OpenCV實現和Numpy實現的對比

　　影象為下圖：

7.1  使用OpenCV函式實現

　　用OpenCV函式實現直方圖均衡化很簡單，只需要呼叫一個函式即可：

def opencv_equalizeHist(image_path):
    img = cv2.imread(image_path, 0)
    equ = cv2.equalizeHist(img)
    cv2.imshow('equ', equ)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

　　這樣就影象均衡化了。效果如下：

7.2，使用Numpy函式實現

　　通過前面的介紹，可以明白直方圖均衡化就是用一種特殊的查詢表來實現的，所以這裡用Numpy函式，以查詢表的方式手動來實現影象直方圖均衡化：

def numpy_equalizeHist(image_path):
    img = cv2.imread(image_path, 0)
    # 建立空的查詢表
    lut = np.zeros(256, dtype=img.dtype)

    hist, bins = np.histogram(img.flatten(), 256, [0, 256])
    # 計算累計直方圖
    cdf = hist.cumsum()
    # 除以直方圖中的0值
    cdf_m = np.ma.masked_equal(cdf, 0)
    #等同於前面介紹的lut[i] = int(255.0 *p[i])公式
    cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())
    #將掩模處理掉的元素補為0
    cdf = np.ma.filled(cdf_m, 0).astype('uint8')
    # 計算
    result2 = cdf[img]
    # result = cv2.LUT(img, cdf)

    # cv2.imshow("OpenCVLUT", result)
    cv2.imshow("NumPyLUT", result2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

　　結果如下：

7.3，三種方法的直方圖對比

　　這裡對比了使用查詢表，使用OpenCV，使用numpy直方圖均衡化生成的直方圖：

　　（注意：這裡有將三種方法生成的直方圖均衡化的圖片儲存下來，然後對此均衡化的圖片畫直方圖）

import cv2
import numpy as np
import matplotlib.pyplot as plt


def LookUpTable(photo_path):
    image = cv2.imread(photo_path, 0)
    # 建立空的查詢表
    lut = np.zeros(256, dtype=image.dtype)
    # OpenCV提供了cv.calcHist()函式來獲取直方圖
    hist = cv2.calcHist([image],  # 計算影象的直方圖
                        [0],  # 使用的通道
                        None,  # 沒有使用mask
                        [256],  # it is a 2D histogram
                        [0.0, 255.0])
    # print(hist.shape)  # (256, 1)
    minBinNo, maxBinNo = 0, 255

    # 計算從左起第一個不為0的直方圖位置
    for binNo, binValue in enumerate(hist):
        if binValue != 0:
            minBinNo = binNo
            break

    # 計算從右起第一個不為0的直方圖位置
    for binNo, binValue in enumerate(reversed(hist)):
        if binValue != 0:
            maxBinNo = 255 - binNo
            break

    # 生成查詢表
    for i, v in enumerate(lut):
        if i < minBinNo:
            lut[i] = 0
        elif i > maxBinNo:
            lut[i] = 255
        else:
            lut[i] = int(255.0 * (i - minBinNo) / (maxBinNo - minBinNo) + 0.5)

    # 計算
    lut = cv2.LUT(image, lut)
    cv2.imwrite('lut.jpg', lut)
    # cv2.imshow('lut', lut)
    # cv2.waitKey(0)
    # cv2.destroyAllWindows()
    return lut


def opencv_equalizeHist(image_path):
    img = cv2.imread(image_path, 0)
    equ = cv2.equalizeHist(img)
    cv2.imwrite('equ.jpg', equ)
    # cv2.imshow('equ', equ)
    # cv2.waitKey(0)
    # cv2.destroyAllWindows()
    return equ


def numpy_equalizeHist(image_path):
    img = cv2.imread(image_path, 0)
    hist, bins = np.histogram(img.flatten(), 256, [0, 256])
    # 計算累計直方圖
    cdf = hist.cumsum()
    # 除以直方圖中的0值
    cdf_m = np.ma.masked_equal(cdf, 0)
    # 等同於前面介紹的lut[i] = int(255.0 *p[i])公式
    cdf_m = (cdf_m - cdf_m.min()) * 255 / (cdf_m.max() - cdf_m.min())
    # 將掩模處理掉的元素補為0
    cdf = np.ma.filled(cdf_m, 0).astype('uint8')
    # 計算
    numpy_lut = cdf[img]
    cv2.imwrite('numpy_lut.jpg', numpy_lut)
    # cv2.imshow("NumPyLUT", numpy_lut)
    # cv2.waitKey(0)
    # cv2.destroyAllWindows()
    return numpy_lut


def show_allphoto():
    lut = cv2.imread('lut.jpg', 0)
    np_equ = cv2.imread('numpy_lut.jpg', 0)
    opencv_equ = cv2.imread('equ.jpg', 0)
    print(lut.shape,  np_equ.shape, opencv_equ.shape)

    lut = cv2.calcHist([lut], [0], None, [256], [0.0, 256.0])
    np_equ = cv2.calcHist([np_equ], [0], None, [256], [0.0, 256.0])
    opencv_equ = cv2.calcHist([opencv_equ], [0], None, [256], [0.0, 256.0])

    plt.subplot(311), plt.plot(lut)
    plt.subplot(312), plt.plot(np_equ)
    plt.subplot(313), plt.plot(opencv_equ)
    plt.show()



if __name__ == '__main__':
    photo_path = 'wiki.jpg'
    # lut = LookUpTable(photo_path)
    # np_equ = numpy_equalizeHist(photo_path)
    # opencv_equ = opencv_equalizeHist(photo_path)
    show_allphoto()

　　結構如下：

 　　lut計算出來的和opencv和numpy計算的結果還是不太一樣。但是 opencv和numpy計算的結果相似。具體原因不知道，再學習。

 https://blog.csdn.net/sunny2038/article/details/9403059

https://blog.csdn.net/v_xchen_v/article/details/7991