如果需要處理的原圖及程式碼，請移步小編的GitHub地址

　　傳送門：請點選我

　　如果點選有誤：https://github.com/LeBron-Jian/ComputerVisionPractice

準備：影象轉陣列，陣列轉影象

　　將RGB影象轉換為一維陣列的程式碼如下：

# 影象二維畫素轉換為一維
img = cv2.imread(filename=img_path)
data = img.reshape((-1, 3))
data = np.float32(data)
print(img.shape, data.shape)

 　　我們打印出來結果，看看如下：

(67, 142, 3) (9514, 3)

 　　當我們處理完後，再將影象轉換回uint8二維型別，程式碼如下：

# 影象轉換回uint8二維型別
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))

# 影象轉換為RGB顯示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

1，影象量化處理

　　影象通常是自然界景物的客觀反映，並以照片形式或視訊記錄的介質連續儲存，獲取影象的目標是從感知的資料中產生數字影象，因此需要把連續的影象資料離散化，轉換為數字化影象，其工作主要包括兩方面——量化和取樣。數字化幅度值稱為量化，數字化座標值稱為取樣。

　　下面主要學習影象量化和取樣處理的概念，並通過Python和OpenCV實現這些功能。

1.1  影象量化概述

　　所謂量化（Quantization），就是將影象畫素點對應亮度的連續變換區間轉換為單個特定值的過程，即將原始灰度影象的空間座標幅度值離散化。量化等級越多，影象層次越豐富，灰度解析度越高，影象的質量也越好；量化等級越少，影象層次欠豐富，灰度解析度越低，會出現影象輪廓分層的現象，降低了影象的質量，下圖是將影象的連續灰度值轉換為0到255的灰度級的過程。

　　量化後，影象就被表示成一個整數矩陣，每個畫素具有兩個屬性：位置和灰度。位置由行，列表示。灰度表示該畫素位置上亮暗程度的整數。此數字矩陣M*N就作為計算機處理的物件了，灰度級一般為0~255（8bit量化）。如果量化等級為2，則將使用兩種灰度級表示原始影象的畫素（0~255），灰度值小於128的取0，大於等於128的取128；如果量化等級為4，則將使用四種灰度級表示原始影象的畫素，新影象將分層為四種顏色，0~64區間取0,64~128區間取64,128~192區間的取128,192~255區間取192，依次類推。

1.1.1  影象彩色量化（減色處理）簡介

　　RGB 的畫素值在 0~255之間，我們想要用更少的記憶體空間表徵一張影象時怎麼辦呢？首先是減色處理，將影象用 32， 96， 160， 224 這 4 個畫素值表示。即將影象由256³壓縮至4³，RGB的值只取{32,96,160,224}，這被稱作色彩量化。

1.2  影象量化的程式碼實現

　　下面學習Python影象量化處理相關程式碼湊在哦，其核心流程是建立一張臨時圖片，接著迴圈遍歷原始影象中所有畫素點，判斷每個畫素點應該屬於的量化等級，最後將臨時影象展示，下面程式碼學習將灰度影象轉換為兩種量化等級。

　　程式碼如下：

#_*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取圖片
img = cv2.imread('kd2.jpg')
# 獲取影象的高度和寬度
height, width = img.shape[0], img.shape[1]

# 建立一幅影象，內容使用零填充
new_img = np.zeros((height, width, 3), np.uint8)

# 影象量化操作，量化等級為2
for i in range(height):
    for j in range(width):
        for k in range(3):  # 對應BGR三通道
            if img[i, j][k] < 128:
                gray = 0
            else:
                gray = 129
            new_img[i, j][k] = np.uint8(gray)

# 顯示影象
cv2.imshow('src', img)
cv2.imshow('new', new_img)
# 等待顯示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　下圖是輸出結果，它將影象劃分為兩種量化等級。

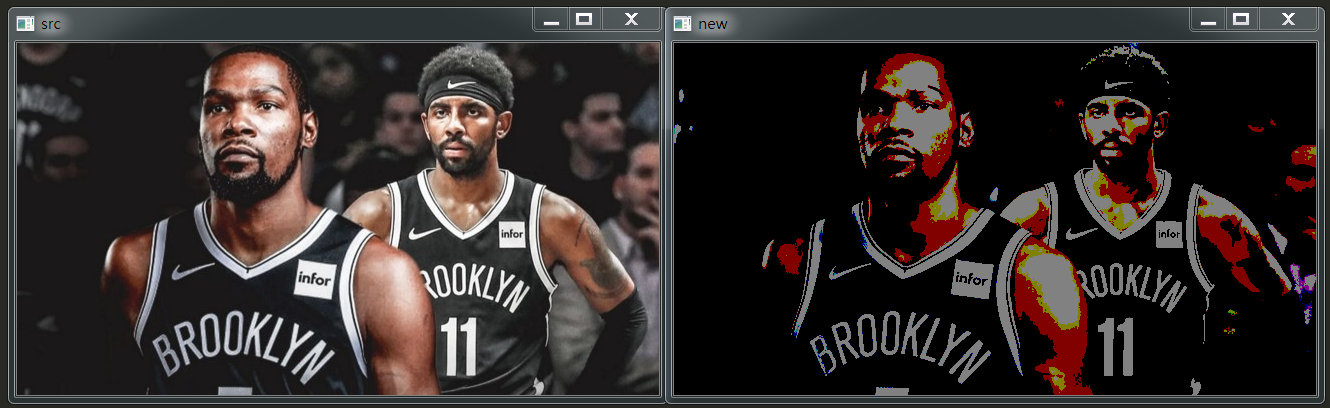
 　　下面的程式碼分別比較了量化等級為2， 4， 8 的量化處理效果。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取圖片
img = cv2.imread('kd2.jpg')
# 獲取影象的高度和寬度
height, width = img.shape[0], img.shape[1]

# 建立一幅影象，內容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)
new_img2 = np.zeros((height, width, 3), np.uint8)
new_img3 = np.zeros((height, width, 3), np.uint8)

# 影象量化操作，量化等級為2
for i in range(height):
    for j in range(width):
        for k in range(3):  # 對應BGR三通道
            if img[i, j][k] < 128:
                gray = 0
            else:
                gray = 129
            new_img1[i, j][k] = np.uint8(gray)

# 影象量化操作，量化等級為4
for i in range(height):
    for j in range(width):
        for k in range(3):  # 對應BGR三通道
            if img[i, j][k] < 64:
                gray = 0
            elif img[i, j][k] < 128:
                gray = 64
            elif img[i, j][k] < 192:
                gray = 128
            else:
                gray = 192
            new_img2[i, j][k] = np.uint8(gray)

# 影象量化操作，量化等級為8
for i in range(height):
    for j in range(width):
        for k in range(3):  # 對應BGR三通道
            if img[i, j][k] < 32:
                gray = 0
            elif img[i, j][k] < 64:
                gray = 32
            elif img[i, j][k] < 96:
                gray = 64
            elif img[i, j][k] < 128:
                gray = 96
            elif img[i, j][k] < 160:
                gray = 128
            elif img[i, j][k] < 192:
                gray = 160
            elif img[i, j][k] < 224:
                gray = 192
            else:
                gray = 224
            new_img3[i, j][k] = np.uint8(gray)

# 用來正常顯示中文標籤
plt.rcParams['font.sans-serif'] = ['SimHei']

# 顯示影象
titles = [u'(a)原始影象', u'(b)量化L2', u'(c)量化L4', u'(d)量化L8', ]
images = [img, new_img1, new_img2, new_img3]
for i in range(4):
    plt.subplot(2, 2, i+1), plt.imshow(images[i])
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　結果如下：

1.3，影象分割與聚類概述

1.3.1  影象分割的定義

　　影象分割是影象識別和計算機視覺至關重要的預處理方法。影象分割就是把影象分成若干個特定的，具有獨特性質的區域並提出感興趣目標的技術和過程。它是由影象處理到影象分析的關鍵步驟。現有的影象分割方法主要分為以下幾類：基於閾值的分割方法，基於區域的分割方法，基於邊緣的分割方法以及基於特定理論的分割方法等。從數學角度來看，影象分割是將數字影象劃分成互不相交的區域的過程。影象分割的過程也是一個標記過程，即把屬於同一區域的畫素賦予相同的編號。

1.3.2  聚類的定義

　　一個聚類就是一組資料物件的集合，集合內各物件彼此相似，各集合間的物件彼此相差較大。將一組物理或抽象物件中類似的物件組織成若干組的過程就稱為聚類過程。然而在聚類的過程中，我們涉及到的物件的資料型別除了常用的間隔數值屬性，二值屬性，符號，順序，比例數值屬性，混合型別屬性等外，還可能遇到影象，音訊，視訊等多媒體資料物件。對於傳統的資料型別已經有了很多成熟的計算距離方法，這些方法包括：歐式，Manhattan，Minkowski距離公式，二值變數距離比較公式等等。然而對於多媒體資料物件，由於其特殊性，一致沒有一個很好地演算法對其進行分類。

　　聚類是一個將資料集劃分為若干簇或類的過程，並使得同一簇內的資料物件具有較高的相似度，而不同組中的資料物件則是不相似的。相似或不相似的度量是基於資料物件描述屬性的取值來確定的。通常是利用（各物件間）距離來進行描述。

　　下面要學習的是基於理論的影象影象分割方法，通過 K-Means聚類演算法實現影象分割或顏色分層處理。

1.4，K-Means 聚類量化處理

1.4.1  K-Means 聚類量化處理原理

　　K-Means 聚類是最常用的聚類演算法，最初起源於訊號處理，其目的是將資料點劃分為 K 個類簇，找到每個簇的中心並使其度量最小化。該演算法的最大優點是簡單，便於理解，運算速度較快，缺點是隻能應用於連續性資料，並且要在聚類前指定聚類的類簇數。

　　如果想了解K-Means演算法的原理，請參考我這篇部落格：

Python機器學習筆記：K-Means演算法，DBSCAN演算法

　　下面是 K-Means 聚類演算法的分析流程，步驟如下：

• 第一步，確定K值，即將資料集聚整合K個類簇或小組。
• 第二步，從資料集中隨機選擇K個數據點作為質心（Centroid）或資料中心。
• 第三步，分別計算每個點到每個質心之間的距離，並將每個點劃分到離最近質心的小組，跟定了那個質心。
• 第四步，當每個質心都聚集了一些點後，重新定義演算法選出新的質心。
• 第五步，比較新的質心和老的質心，如果新質心和老質心之間的距離小於某一個閾值，則表示重新計算的質心位置變化不大，收斂穩定，則認為聚類已經達到了期望的結果，演算法終止。
• 第六步，如果新的質心和老的質心變化很大，即距離大於閾值，則繼續迭代執行第三步到第五步，直到演算法終止。

　　下圖是對身高和體重進行聚類的演算法，將資料集的人群聚類成三類。

1.4.2  K-Means 聚類opencv原始碼

　　在opencv中，KMeans() 函式原型如下所示：

retval, bestLabels, centers = kmeans(data, K, bestLabels, criteria, attempts, 
flags[, centers])

　　函式內變數的含義：

• data表示聚類資料，最好是np.flloat32型別的N維點集，之所以是 np.float32 原因是這種資料型別運算速度快，同樣的資料下如果是 uint型資料將會特別慢。
• K表示聚類類簇數，opencv的kmeans分類是需要已知分類數的。
• bestLabels表示預設的分類標籤，即輸出的整數陣列，用於儲存每個樣本的聚類標籤索引，沒有的話為None
• criteria表示演算法終止條件，即最大迭代次數或所需精度。在某些迭代中，一旦每個簇中心的移動小於criteria.epsilon，演算法就會停止，迭代停止的選擇是一個含有三個元素的元組型數，格式為（type,  max_iter, epsilon），其中 type 有兩種選擇：

　　　　——cv2.TERM_CRITERIA_EPS：精確度（誤差）滿足 epsilon停止

　　　　——cv2.TERM_CRITERIA_MAX_ITER：迭代次數超過 max_iter 停止

　　　　——cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER，兩者合體，任意一個滿足結束。

• attempts表示重複試驗kmeans演算法的次數，演算法返回產生最佳緊湊性的標籤
• flags表示初始中心的選擇，兩種方法是cv2.KMEANS_PP_CENTERS ;和cv2.KMEANS_RANDOM_CENTERS
• centers表示叢集中心的輸出矩陣，每個叢集中心為一行資料

1.4.3  K-Means 聚類分割灰度影象

　　在影象處理中，通過 K-Means聚類演算法可以實現影象分割，影象聚類，影象識別等操作，下面主要用來進行影象顏色分割。假設存在一張 100*100畫素的灰度影象，它由 10000 個RGB灰度級組成，我們通過 K-Menas 可以將這些畫素點聚類成 K 個簇，然後使用每個簇內的置心點來替換簇內所有的畫素點，這樣就能實現在不改變解析度的情況下量化壓縮影象顏色，實現影象顏色層級分割。

　　下面使用該方法對灰度影象顏色進行分割處理，需要注意，在進行 K-Means 聚類操作之前，需要將 RGB畫素點轉換成一維的陣列，再講各形式的顏色聚集在一起，形成最終的顏色分割。

# _*_coding:utf-8_*_
# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取原始影象灰度顏色
img = cv2.imread('scenery.jpg', 0)
print(img.shape)

# 獲取影象高度、寬度
rows, cols = img.shape[:]

# 影象二維畫素轉換為一維
data = img.reshape((rows * cols, 1))
data = np.float32(data)

# 定義中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 設定標籤
flags = cv2.KMEANS_RANDOM_CENTERS

# K-Means聚類 聚整合4類
compactness, labels, centers = cv2.kmeans(data, 4, None, criteria, 10, flags)

# 生成最終影象
dst = labels.reshape((img.shape[0], img.shape[1]))

# 用來正常顯示中文標籤
plt.rcParams['font.sans-serif'] = ['SimHei']

# 顯示影象
titles = [u'灰度影象', u'聚類影象']
images = [img, dst]
for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray'),
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　原圖如下：

 　　輸出結果如下所示，左邊為灰度圖，右邊為K-Means聚類後的影象，它將相似的顏色或區域聚集到一起。

 　　人物圖如下：

 　　效果如下：

1.4.4  K-Means 聚類對比分割彩色影象

　　下面程式碼是對彩色影象進行顏色分割處理，它將彩色影象聚類成2類，4類和64類。

# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取原始影象
img = cv2.imread('scenery.jpg')
print(img.shape)

# 影象二維畫素轉換為一維
data = img.reshape((-1, 3))
data = np.float32(data)

# 定義中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 設定標籤
flags = cv2.KMEANS_RANDOM_CENTERS

# K-Means聚類 聚整合2類
compactness, labels2, centers2 = cv2.kmeans(data, 2, None, criteria, 10, flags)

# K-Means聚類 聚整合4類
compactness, labels4, centers4 = cv2.kmeans(data, 4, None, criteria, 10, flags)

# K-Means聚類 聚整合8類
compactness, labels8, centers8 = cv2.kmeans(data, 8, None, criteria, 10, flags)

# K-Means聚類 聚整合16類
compactness, labels16, centers16 = cv2.kmeans(data, 16, None, criteria, 10, flags)

# K-Means聚類 聚整合64類
compactness, labels64, centers64 = cv2.kmeans(data, 64, None, criteria, 10, flags)

# 影象轉換回uint8二維型別
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))

centers4 = np.uint8(centers4)
res = centers4[labels4.flatten()]
dst4 = res.reshape((img.shape))

centers8 = np.uint8(centers8)
res = centers8[labels8.flatten()]
dst8 = res.reshape((img.shape))

centers16 = np.uint8(centers16)
res = centers16[labels16.flatten()]
dst16 = res.reshape((img.shape))

centers64 = np.uint8(centers64)
res = centers64[labels64.flatten()]
dst64 = res.reshape((img.shape))

# 影象轉換為RGB顯示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
dst2 = cv2.cvtColor(dst2, cv2.COLOR_BGR2RGB)
dst4 = cv2.cvtColor(dst4, cv2.COLOR_BGR2RGB)
dst8 = cv2.cvtColor(dst8, cv2.COLOR_BGR2RGB)
dst16 = cv2.cvtColor(dst16, cv2.COLOR_BGR2RGB)
dst64 = cv2.cvtColor(dst64, cv2.COLOR_BGR2RGB)

# 用來正常顯示中文標籤
plt.rcParams['font.sans-serif'] = ['SimHei']

# 顯示影象
titles = [u'原始影象', u'聚類影象 K=2', u'聚類影象 K=4',
          u'聚類影象 K=8', u'聚類影象 K=16', u'聚類影象 K=64']
images = [img, dst2, dst4, dst8, dst16, dst64]
for i in range(6):
    plt.subplot(2, 3, i + 1), plt.imshow(images[i], 'gray'),
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　我們依然採用上面的圖：

2，影象取樣處理

2.1 影象取樣處理概述

　　影象取樣（Image Sampling）是將一幅連續影象在空間上分割成 M*N 個網格，每個網格用一個亮度值或灰度值來表示，其示意圖如下所示：

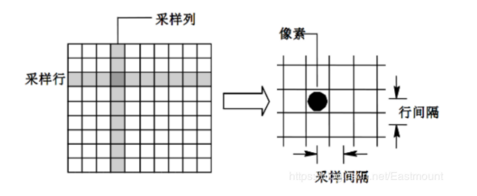
 　　影象取樣的間隔越大，所得影象畫素數越少，空間解析度越低，影象質量越差，甚至出現馬賽克效益；相反，影象取樣的間隔越小，所得影象畫素數越多，空間解析度越高，影象質量越好，但資料量會相應的增大。

　　馬賽克原理：將影象中選中區域的畫素值用這個選中區域中的某一畫素值或者隨機值替換。

　　下圖中將指定區域的畫素點值，全部改為左上角第一個點的畫素點值：

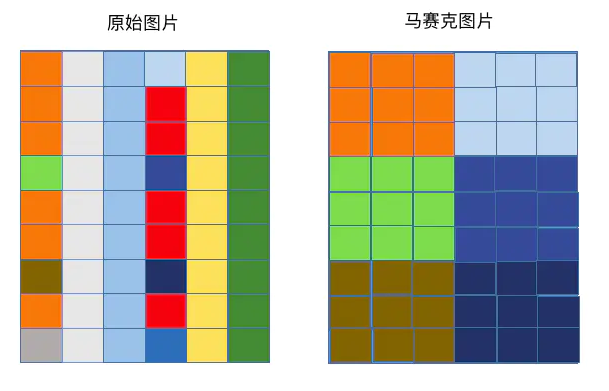
2.2  影象取樣Python實現

　　下面學習Python影象取樣處理相關程式碼操作。其核心流程是建立一張臨時圖片，設定需要採用的區域大小（如 16*16），接著迴圈遍歷原始影象中所有畫素點，取樣區域內的畫素點賦值相同（如左上角畫素點的灰度值），最終實現影象取樣處理。程式碼是進行16*16取樣的過程。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取圖片
img = cv2.imread('kd2.jpg')

# 獲取影象的高度和寬度
height, width = img.shape[0], img.shape[1]
# print(img.shape)  # (352, 642, 3)
# 取樣轉換成 16*16 區域
numHeight, numWidth = height / 16, width / 16

# 建立一幅影象，內容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)

# 影象迴圈取樣 16*16 區域
for i in range(16):
    # 獲取Y座標
    y = int(i * numHeight)
    for j in range(16):
        # 獲取 X 座標
        x = int(j * numWidth)
        # 獲取填充顏色，左上角畫素點
        b = img[y, x][0]
        g = img[y, x][1]
        r = img[y, x][2]

        # 迴圈設定小區域取樣
        for n in range(int(numHeight)):
            for m in range(int(numWidth)):
                new_img1[y+n, x+m][0] = np.uint8(b)
                new_img1[y+n, x+m][1] = np.uint8(g)
                new_img1[y+n, x+m][2] = np.uint8(r)

# 顯示影象
cv2.imshow('src', img)
cv2.imshow('new src', new_img1)
# 等待顯示
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　結果如下：

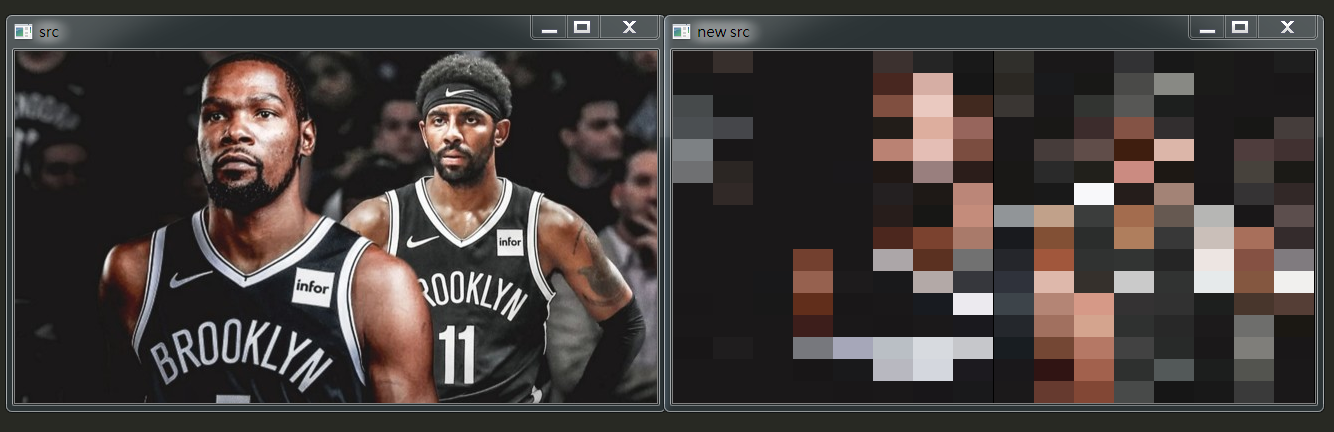
 　　同樣，可以對彩色圖片進行取樣處理，下面的程式碼將彩色風景取樣處理成 8*8的馬賽克區域。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取圖片
img = cv2.imread('kd2.jpg')

# 獲取影象的高度和寬度
height, width = img.shape[0], img.shape[1]
# print(img.shape)  # (352, 642, 3)
# 取樣轉換成 8*8 區域
numHeight, numWidth = height / 8, width / 8

# 建立一幅影象，內容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)

# 影象迴圈取樣 8*8 區域
for i in range(8):
    # 獲取Y座標
    y = int(i * numHeight)
    for j in range(8):
        # 獲取 X 座標
        x = int(j * numWidth)
        # 獲取填充顏色，左上角畫素點
        b = img[y, x][0]
        g = img[y, x][1]
        r = img[y, x][2]

        # 迴圈設定小區域取樣
        for n in range(int(numHeight)):
            for m in range(int(numWidth)):
                new_img1[y+n, x+m][0] = np.uint8(b)
                new_img1[y+n, x+m][1] = np.uint8(g)
                new_img1[y+n, x+m][2] = np.uint8(r)

# 顯示影象
cv2.imshow('src', img)
cv2.imshow('new src', new_img1)
# 等待顯示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　結果如下：

 　　但是上述程式碼存在一個問題，就是當圖片的長度和寬度不能被取樣區域整除時，輸出影象的最右邊和最下邊的區域沒有被取樣處理。這裡推薦大家做一個求餘運算，將不能整除部分的區域也進行取樣處理。

2.3   區域性馬賽克處理

　　前面學習了對整幅影象做了取樣處理，那麼如何對影象的區域性區域進行馬賽克處理呢？

　　實現用按下滑鼠左鍵拖動時，在滑鼠經過的路徑上打上馬賽克，而馬賽克的原理是將影象中選中區域的畫素用這個選中區域中的某一畫素覆蓋，為了不讓滑鼠重複經過影象中同一個的時候，選取不一樣的畫素，該程式將在輸入圖片的時候，就實現了全圖的馬賽克效果。而當滑鼠劃過的時候，程式只是將實現馬賽克的影象的指定位置複製到顯示的影象中。

　　下面程式碼實現了該功能，當滑鼠按下時，它能夠給滑鼠拖動的區域打上馬賽克，並按下 “s”鍵儲存影象到本地。

 　　程式碼如下：

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt


# 滑鼠事件
def draw(event, x, y, flags, parma):
    global en
    # 滑鼠左鍵按下開啟 en 鍵
    if event == cv2.EVENT_LBUTTONDOWN:
        en = True
    # 滑鼠左鍵按下並且移動
    elif event == cv2.EVENT_MOUSEMOVE and flags == cv2.EVENT_LBUTTONDOWN:
        # 呼叫函式打馬賽克
        if en:
            drawMask(y, x)
        # 滑鼠左鍵彈起結束操作
        elif event == cv2.EVENT_LBUTTONUP:
            en = False


# 影象區域性採用操作
def drawMask(x, y, size=10):
    # size*size 取樣處理
    m = int(x / size * size)
    n = int(y / size * size)
    # 10*10 區域設定為同一畫素值
    for i in range(int(size)):
        for j in range(int(size)):
            img[m+i][n+j] = img[m][n]

if __name__ == '__main__':
    # 讀取原始影象
    img = cv2.imread('durant.jpg')
    # 設定滑鼠右鍵開啟
    en = False

    # 開啟對話方塊
    cv2.namedWindow('image')
    # 呼叫draw 函式設定滑鼠操作
    cv2.setMouseCallback('image', draw)

    # 迴圈處理
    while(1):
        cv2.imshow('image', img)
        # 按 ESC鍵退出
        if cv2.waitKey(10) & 0xFF == 27:
            break
        # 按 s 鍵儲存圖片
        elif cv2.waitKey(10) & 0xFF == 115:
            cv2.imwrite('save.jpg', img)
    # 退出視窗
    cv2.destroyAllWindows()

　　打了馬賽克的圖片如下：

 　　我將他的號碼打碼了。

參考文獻：https://blog.csdn.net/Eastmount/article/details/89218513

https://blog.csdn.net/Eastmount/article/details/8928