如果需要處理的原圖及程式碼，請移步小編的GitHub地址

　　傳送門：請點選我

　　如果點選有誤：https://github.com/LeBron-Jian/ComputerVisionPractice

　　在數字影象處理中，有兩個經典的變換被廣泛應用——傅立葉變換和霍夫變化。其中，傅立葉變換主要是將時間域上的訊號轉變為頻率域上的訊號，用來進行影象降噪，影象增強等處理，這一篇主要學習傅立葉變換，後面在學習霍夫變換。

　　下面學習一下傅立葉變換。有人說傅立葉分析不僅僅是一個數學工具，更是一種可以徹底顛覆一個人以前世界觀的思維模式（出處（強烈建議看這篇文章）：https://zhuanlan.zhihu.com/p/19763358）

　　傅立葉變換的作用：

　　對於數字影象這種離散的訊號，頻率大小表示訊號變換的劇烈程度或者說訊號變化的快慢。頻率越大，變換越劇烈，頻率越小，訊號越平緩，對應到的影象中，高頻訊號往往是影象中的邊緣訊號和噪聲訊號，而低頻訊號包含影象變化頻繁的影象輪廓及背景燈訊號。

　　需要說明的是：傅立葉變換得到的頻譜圖上的點與原影象上的點之間不存在一一對應的關係。

• 高頻：變換劇烈的灰度分量，例如邊界
• 低頻：變換緩慢的灰度分量，例如一片大海

　　濾波器：

• 低通濾波器：只保留低頻，會使得影象模糊
• 高頻濾波器：只保留高頻，會使得影象細節增強

　　不懂的話，可以看之前文章中貼上的一幅圖，這裡再貼上一下：

具體模糊和濾波的關係如下圖（https://www.zhihu.com/question/54918332/answer/142137732）：

1，頻域及其頻域資料的應用

1.1  什麼是頻域

　　從我們出世，我們看到的世界都是以時間貫穿，股票的走勢，人的身高，汽車的軌跡都會隨著時間發生變換。這種以時間作為參照來觀察動態世界的方法我們稱其為時域分析。而我們也想當然的認為，世間萬物都在隨著時間不停的改變，並且永遠不會停止下來。但是我們可以用另一種方法觀察世界的話，你可以發現世界是永恆不變的，而這個靜止的世界就叫做頻域。

　　正式定義：頻域是描述訊號在頻率方面特性時用到的一種座標系。在電子學，控制系統工程和統計學中，頻域圖顯示了一個在頻率範圍內每個給定頻帶內的訊號量。

　　下面舉個例子：

　　我們普通人對音樂的理解是什麼呢？可能如下圖：

　　上圖是我們對音樂最普遍的理解，一個隨著時間變化的震動。但是我相信對於樂手來說，音樂更直觀的理解是這樣的：

 　　下面我們將兩個圖簡化，借用百度百科的正弦函式在時域和頻域的表現如下：

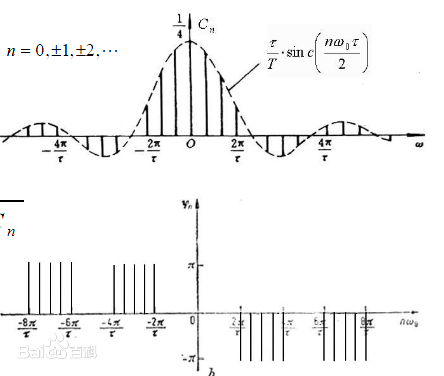
　　總結來說，在時域我們觀察到鋼琴的琴絃一會上一會下的擺動，如同上圖上一樣的走勢，而在頻域，就只是永恆的，如上圖下一樣。而貫穿時域與頻域的方法之一，就是傅立葉分析。傅立葉分析可分為傅立葉級數（Fourier Serie）和傅立葉變換（Fourier Transformation）。

1.2  頻域資料的應用

影象去噪

　　我們可以根據需要獲得在頻域對影象進行處理，比如在需要除去影象中的噪聲時，我們可以設計一個低通濾波器，去掉影象中的高頻噪聲，但是往往也會抑制影象的邊緣資訊，這就是造成影象模糊的原因。以均值濾波為例，用均值模板與影象做卷積，大家都知道，在空間域做卷積，相當於在頻域做乘積，而均值模板在頻域是沒有高頻訊號的，只有一個常量的分量，所以均值模板是對影象區域性做低通濾波。除此之外，常見的高斯濾波也是一種低通濾波器，因為高斯函式經過傅立葉變換後，在頻域的分佈依然服從高斯分佈，如下圖所示，所以它對高頻資訊有很好的濾除效果。

影象增強及銳化

　　影象增強需要增強影象的細節，而影象的細節往往就是影象中高頻的部分，所以增強影象中的高頻資訊能夠達到影象增強的目的。

　　同樣的影象銳化的目的是使模糊的影象變得更加清晰，其主要方式是增強影象的邊緣部分，其實就是增強影象中灰度變化劇烈的部分，所以通過增強影象中的高頻資訊能夠增強影象邊緣，從而達到影象銳化的目的。從這裡可以看出，可以通過提取影象中的高頻訊號來得到影象的邊緣和紋理資訊。

2，傅立葉變換原理

2.1 舉例分析傅立葉變換

　　傅立葉變換（Fourier Transform，簡稱FT）常用於數字訊號處理，它的目的是將時間域上的訊號轉變為頻率域上的訊號。隨著域的不同，對同一個事物的瞭解角度也隨之改變，因此在時域某些不好處理的地方，在頻域就可以較為簡單的處理。同時，可以從頻域裡發現一些原先不易察覺的特徵。傅立葉定理指出“任何連續週期訊號都可以表示成（或者無限逼近）一系列正弦訊號的疊加”。

 　　下面引用“Python + OpenCV影象處理課程”（地址在文末給出）中的一個案例，他將某飲料的製作過程的時域角度轉換為頻域角度。

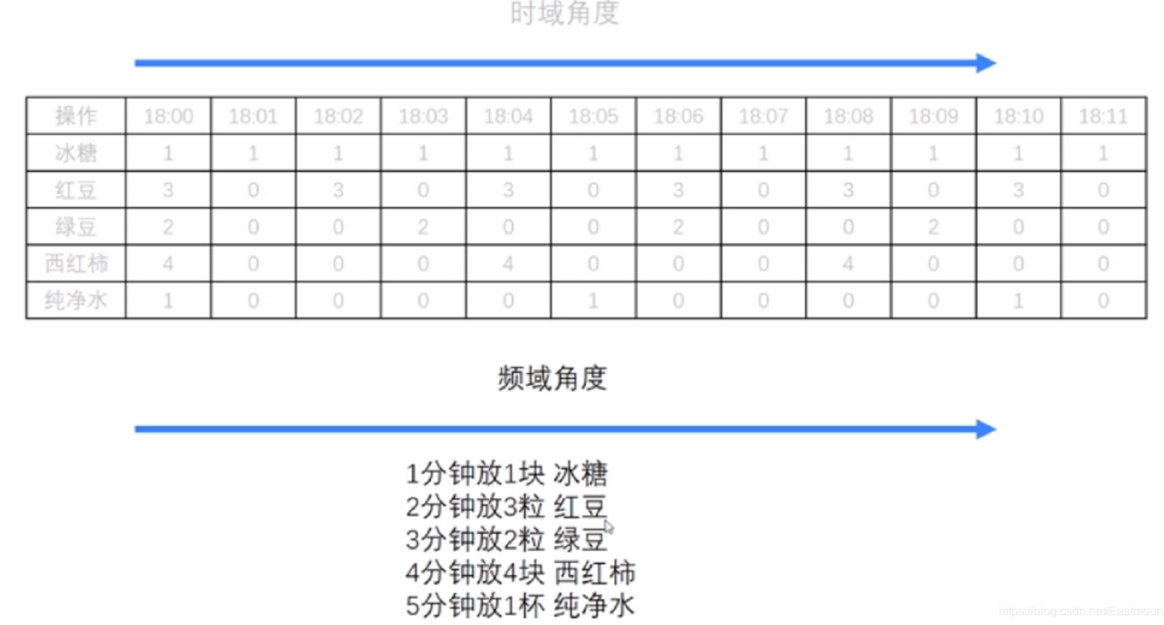
 　　繪製對應的時間圖和頻率圖如下所示：

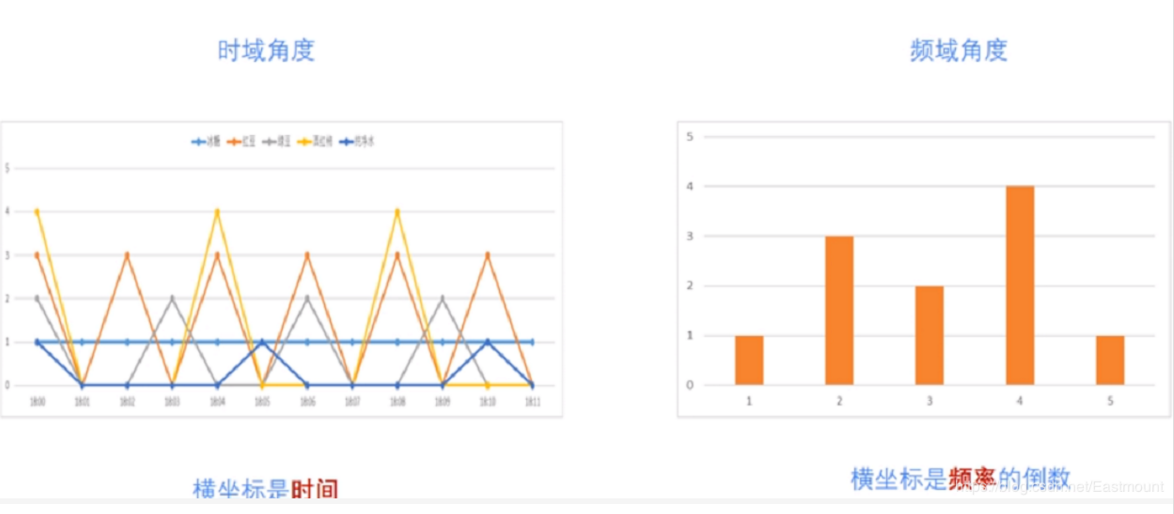
 　　傅立葉公式如下，其中 w 表示頻率，t 表示時間，為複變函式。它將時間域的函式表示為頻率域的函式 f(t) 的積分。

　　傅立葉變換認為一個周期函式（訊號）包含多個頻率分量，任意函式（訊號） f(t) 可通過多個周期函式（或基函式）相加合成。從物理角度理解，傅立葉變換是以一組特殊的函式（三角函式）為正交基，對原函式進行線性變換，物理意義便是原函式在各組基函式的投影。如下圖所示，它是由三條正弦曲線組成：

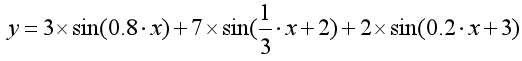
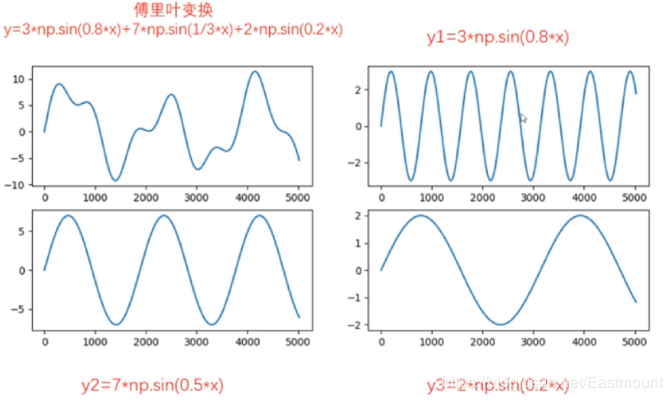　　傅立葉變換可以應用於影象處理中，經過對影象進行變換得到其頻譜圖。從頻譜圖裡頻率高低來表徵影象中灰度變化劇烈程度。影象中的邊緣訊號和噪聲訊號往往是高頻訊號，而影象變換頻繁的影象輪廓及背景等訊號往往是低頻訊號。這時可以有針對性的對影象進行相關操作，例如影象除噪，影象增強和銳化等。

　　二維影象的傅立葉變換可以用以下數學公式表示，其中 f 是空間域（Spatial Domain）的值， F 是頻域（Frequency Domain）值

2.2  二維傅立葉變換的定義

　　上面其實已經引出了二維傅立葉變換，這裡詳細學習一下。

　　首先我們看一下連續型二維傅立葉變換：

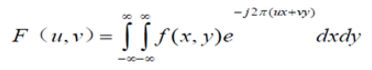
　　連續型二維傅立葉變換的逆變換：

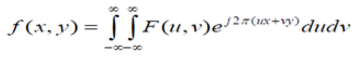
　　下面看一下離散型二維傅立葉變換（當我們定義影象尺寸為M*N，則函式的離散傅立葉變換由以下等式給出）：

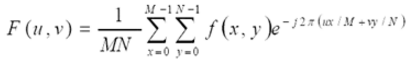
　　離散傅立葉逆變換由下式給出：

　　令R和I分別表示F的實部和虛部，則傅立葉頻譜，相位角，功率譜（幅度）定義如下：

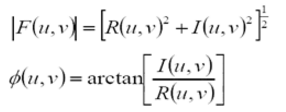
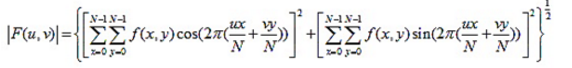
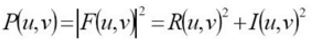
2.3  用 FFT 計算二維離散傅立葉變換

　　二維離散傅立葉變換的定義為：

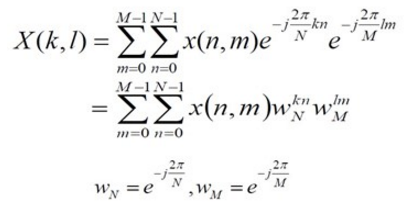　　二維離散傅立葉變換可通過兩次一維離散傅立葉變換來實現：

　　（1）做一維N點DFT（對每個 m 做一次，共 M 次）

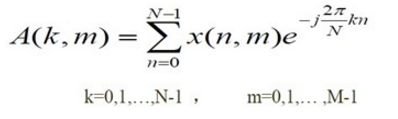
　　（2）作M點的DFT（對每個k做一次，共N次）

　　這兩次離散傅立葉變換都可以用快速演算法求得，若M和N都是2的冪，則可以使用基二FFT演算法，所需要乘法次數為：

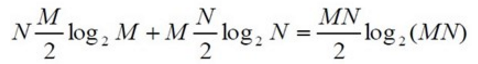
　　而直接計算二維離散傅立葉變換所需要的乘法次數為（M+N）MN，當M和N比較大用FFT運算，可節約很多運算量。

2.4  影象傅立葉變換的物理意義

　　影象的頻率是表徵影象中灰度變換劇烈程度的指標，是灰度在平面空間上的梯度。如：大面積的沙漠在影象中是一片灰度變化緩慢的區域，對應的頻率值很低；而對於地表屬性變換劇烈的邊緣區域在影象中是一片灰度變化劇烈的區域，對應的頻率值較高。傅立葉變換在實際中有明顯的物理意義，設f 是一個能量有限的模擬訊號，則其傅立葉變換就表示 f 的頻譜。從純粹的數學意義上看，傅立葉變換是將一個函式轉換為一系列周期函式來處理的。從物理效果來看，傅立葉變換是將影象從空間域轉換到頻率域，其逆變換是將影象從頻率域轉換到空間域。換句話說，傅立葉變換的物理意義是將影象的灰度分佈函式變換為影象的頻率分佈函式。

　　傅立葉逆變換是將影象的頻率分佈函式變換為灰度分佈函式傅立葉變換以前，影象（未壓縮的點陣圖）是由對在連續空間（現實空間）上的取樣得到一系列的集合，通常用一個二維矩陣表示空間上各點，記為 z=f(x, y)。又因為空間是三維的，影象是二維的，因此空間中物體在另一個維度上的關係就必須由梯度來表示，這樣我們才能通過觀察影象得知物體在三維空間中的對應關係。

　　傅立葉頻譜圖上我們看到的明暗不一的亮點，其意義是指影象上某一點與領域點差異的強弱，即梯度的大小。也即該點的頻率的大小（可以這麼理解，影象中低頻部分指低梯度的點，高頻部分相反）。一般來說，梯度大則該點的亮度強，否則該點的亮度弱。這樣通過觀察傅立葉變換後的頻譜圖，也叫功率圖，我們就可以直觀的看出影象的能量分佈：如果頻譜圖中暗的點數更多，那麼實際影象是比較柔和的（因為各點與領域差異都不大，梯度相對較小）；反之，如果頻譜圖中亮的點數多，那麼實際影象一定是尖銳的，邊界分明且邊界兩邊畫素差異較大的。

　　對頻譜移頻到原點以後，可以看出影象的頻率分佈是以原點為圓心，對稱分佈的。將頻譜移頻到圓心除了可以清晰的看出影象頻率分佈以外，還有一個好處，它可以分離出週期性規律的干擾訊號，比如正弦干擾。一幅頻譜圖如果帶有正弦干擾，移頻到原點上就可以看出，除了中心以外還存在以另一點為中心，對稱分佈的亮點集合，這個集合就是干擾噪音產生的。這時可以很直觀的通過在該位置放置帶阻濾波器消除干擾。

　　對上面的傅立葉變換有了大致的瞭解之後，下面通過Numpy和OpenCV分別學習影象傅立葉變換的演算法及操作程式碼。

2.5  二維傅立葉變換的性質

分離性

　　二維離散傅立葉變換具有分離性

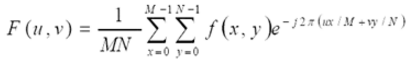
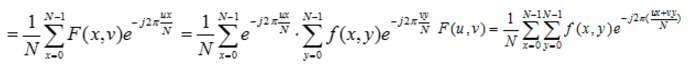
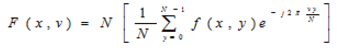
　　分離性質的主要優點是可藉助一系列一維傅立葉變換分兩步求得。第一步，沿著的每一行取變換，將其結果乘以 1/N，取得二維函式；第二步，沿著的每一列取變換，再將結果乘以 1/N就得到了。這種方法是先行後列。如果採用先列後行的順序，其結果相同。

　　如圖：

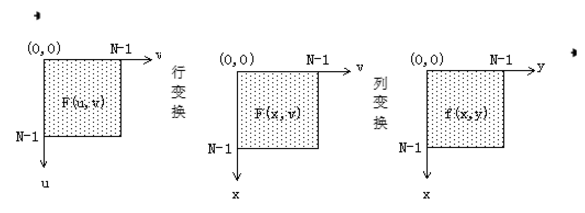
　　對逆變換 f(x, y) 也可以類似的分兩步進行：

 平移性

　　傅立葉變換和逆變換對的位移性質是指：

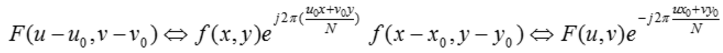
　　由乘以指數項並取其乘積的傅立葉變換，使頻率平面的原點位移至。同樣的，以指數項乘以並取其反變換，將空間域平面的原點位移至當 N/2時，指數項為：

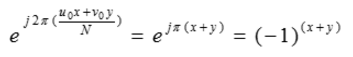
　　即為：

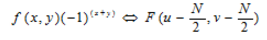
　　這樣，用（x+y）乘以就可以將的傅立葉變換原點移動到 N*N 頻率方陣的中心，這樣才能看到整個譜圖。另外，對的平移不影響其傅立葉變換的幅值。

　　此外，與連續二維傅立葉變換一樣，二維離散傅立葉變換也具有周期性，共軛對稱性，線性，旋轉性，相關定理，卷積定理，比例性等性質。這些性質在分析以及處理影象時有重要意義。

2.6  二維離散傅立葉變換的影象性質

　　1，影象經過二維傅立葉的變換後，其變換稀疏矩陣具有如下性質：若交換矩陣原點設在中心，其頻譜能量集中分佈在變換稀疏矩陣的中心附近。若所用的二維傅立葉變換矩陣的雲巔設在左上角，那麼影象訊號能量將集中在係數矩陣的四個角上。這是由二維傅立葉變換本身性質決定的。同時也表明一股影象能量集中低頻區域。

　　2，影象灰度變化緩慢的區域，對應它變換後的低頻分量部分；影象灰度呈階躍變化的區域，對應變換後的高頻分量部分。除顆粒噪音外，影象細節的邊緣，輪廓處都是灰度變換突變區域，他們都具有變換後的高頻分量特徵。

3，傅立葉變換的實現

　　注意：無論是numpy實現，還是OpenCV實現，得到的結果中頻率為0的部分都會在左上角，通常要轉換到中心位置，可以通過shift變換來實現。

3.1 Numpy實現傅立葉變換

　　Numpy的 FFT 包提供了函式 np.fft.fft2() 可以對訊號進行快速傅立葉變換，其函式原型如下所示（該函式的輸出結果是一個複數陣列complex ndarray）

fft2(a, s=None, axes=(-2, -1), norm=None)

 　　引數意義：

• a表示輸入影象，陣列狀的複雜陣列
• s表示整數序列，可以決定輸出陣列的大小。輸出可選形狀（每個轉換軸的長度），其中s[0]表示軸0，s[1]表示軸1。對應fit(x,n)函式中的n，沿著每個軸，如果給定的形狀小於輸入形狀，則將剪下輸入。如果大於則輸入將用零填充。如果未給定’s’，則使用沿’axles’指定的軸的輸入形狀
• axes表示整數序列，用於計算FFT的可選軸。如果未給出，則使用最後兩個軸。“axes”中的重複索引表示對該軸執行多次轉換，一個元素序列意味著執行一維FFT
• norm包括None和ortho兩個選項，規範化模式（請參見numpy.fft）。預設值為無

　　Numpy中fft模組有很多函式，相關函式如下：

#計算一維傅立葉變換
numpy.fft.fft(a, n=None, axis=-1, norm=None)

#計算二維的傅立葉變換
numpy.fft.fft2(a, n=None, axis=-1, norm=None)

#計算n維的傅立葉變換
numpy.fft.fftn()

#計算n維實數的傅立葉變換
numpy.fft.rfftn()

#返回傅立葉變換的取樣頻率
numpy.fft.fftfreq()

#將FFT輸出中的直流分量移動到頻譜中央
numpy.fft.shift()

 　　下面的程式碼是通過Numpy實現傅立葉變換，呼叫 np.fft.fft2() 快速傅立葉變換得到頻率分佈，接著呼叫 np.fft.fftshift() 函式將中心位置轉移至中間，最終通過 Matplotlib顯示效果圖。

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 讀取影象
img = cv2.imread('irving.jpg', )
# 影象進行灰度化處理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 快速傅立葉變換演算法得到頻率分佈
f = np.fft.fft2(img)

# 預設結果中心點位置是在左上角
# 呼叫fftshift()函式轉移到中間位置
fshift = np.fft.fftshift(f)

# fft 結果是複數，其絕對值結果是振幅
fimg = np.log(np.abs(fshift))

# 展示結果
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('original Fourier')
plt.axis('off')
plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('fourier Fourier')
plt.axis('off')
plt.show()

 　　結果如下：

 　　我們從上面結果看到，左邊為原始影象，右邊為頻率分佈圖譜，其中越靠近中心位置頻率越低，越亮（灰度值越高）的位置代表該頻率的資訊振幅越大。

3.2  OpenCV實現傅立葉變換

　　OpenCV中實現傅立葉變換的函式是 cv2.dft()，他和Numpy輸出的結果是一樣的，但是是雙通道的。第一個通道是結果的實數部分，第二個通道是結果的虛數部分，並且輸入影象要首先轉換成  np.float32格式。其函式原型如下：

dst = cv2.dft(src, dst=None, flags=None, nonzeroRows=None)

 　　引數含義：

• src表示輸入影象，需要通過np.float32轉換格式
• dst表示輸出影象，包括輸出大小和尺寸flags表示轉換標記，其中：

　　　　DFT _INVERSE執行反向一維或二維轉換，而不是預設的正向轉換；

　　　　DFT _SCALE表示縮放結果，由陣列元素的數量除以它；

　　　　DFT _ROWS執行正向或反向變換輸入矩陣的每個單獨的行，該標誌可以同時轉換多個向量，並可用於減少開銷以執行3D和更高維度的轉換等；

　　　　DFT _COMPLEX_OUTPUT執行1D或2D實陣列的正向轉換，這是最快的選擇，預設功能；

　　　　DFT _REAL_OUTPUT執行一維或二維複數陣列的逆變換，結果通常是相同大小的複數陣列，但如果輸入陣列具有共軛複數對稱性，則輸出為真實陣列

• nonzeroRows表示當引數不為零時，函式假定只有nonzeroRows輸入陣列的第一行（未設定）或者只有輸出陣列的第一個（設定）包含非零，因此函式可以處理其餘的行更有效率，並節省一些時間；這種技術對計算陣列互相關或使用DFT卷積非常有用

　　注意：由於輸出的頻譜結果是一個複數，需要呼叫 cv2.magnitude() 函式將傅立葉變換的雙通達結果轉換為0到255的範圍。其函式原型如下：

cv2.magnitude(x, y, magnitude=None)

 　　引數意義：

• x表示浮點型X座標值，即實部
• y表示浮點型Y座標值，即虛部
  最終輸出結果為幅值，即：

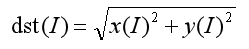
　　完整程式碼如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 讀取影象
img = cv2.imread('irving.jpg', )
# 影象進行灰度化處理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅立葉變換
# cv2.DFT_COMPLEX_OUTPUT 執行一維或二維複數陣列的逆變換，結果通常是相同大小的複數陣列
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)

# 將頻譜低頻從左上角移動到中心位置
dft_shift = np.fft.fftshift(dft)

# 頻譜影象雙通道複數轉換為0~255區間
result = 10 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 顯示影象
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input image')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(result, cmap='gray')
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()

 　　結果如下：

 　　上圖左邊為原始圖，右邊為轉換後的頻譜影象，並且保證低頻位於中心位置。

4，傅立葉逆變換的實現

　　注意：無論是numpy實現，還是OpenCV實現，得到的結果中頻率為0的部分都會在左上角，通常要轉換到中心位置，可以通過shift變換來實現。

4.1 Numpy實現傅立葉逆變換

　　下面介紹 Numpy實現傅立葉逆變換，它是傅立葉變換的逆操作，將頻譜影象轉換為原始影象的過程。通過傅立葉變換將轉換為頻譜圖，並對高頻（邊界）和低頻（細節）部分進行處理，接著需要通過傅立葉逆變換恢復為原始效果圖。頻域上對影象的處理會反映在逆變換影象上，從而更好地進行影象處理。

　　影象傅立葉變換主要使用的函式如下所示：

#實現影象逆傅立葉變換，返回一個複數陣列
numpy.fft.ifft2(a, n=None, axis=-1, norm=None)

#fftshit()函式的逆函式，它將頻譜影象的中心低頻部分移動至左上角
numpy.fft.fftshift()

#將複數轉換為0至255範圍
iimg = numpy.abs(逆傅立葉變換結果)

 　　下面程式碼實現了傅立葉變換和傅立葉逆變換

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 讀取影象
img = cv2.imread('irving.jpg', )
# 影象進行灰度化處理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅立葉變換
# 快速傅立葉變換演算法得到頻率分佈
f = np.fft.fft2(img)
# 預設結果中心點位置是在左上角 呼叫fftshift()函式轉移到中間位置
fshift = np.fft.fftshift(f)
# fft 結果是複數，其絕對值結果是振幅
rimg = np.log(np.abs(fshift))

# 傅立葉逆變換
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)


# 展示結果
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('original Fourier')
plt.axis('off')
plt.subplot(132), plt.imshow(rimg, 'gray'), plt.title('fourier Fourier')
plt.axis('off')
plt.subplot(133), plt.imshow(iimg, 'gray'), plt.title('inverse fourier Fourier')
plt.axis('off')
plt.show()

　　結果如下：

4.2 OpenCV實現傅立葉逆變換

　　在OpenCV中，通過函式 cv2.idft()函式實現傅立葉逆變換，其返回結果取決於原始影象的型別和大小，原始影象可以為複數或實數，同時也要注意輸入影象需要先轉換成 np.float32格式，其函式原型如下：

dst = cv2.idft(src[, dst[, flags[, nonzeroRows]]])

 　　引數意義：

• src表示輸入影象，包括實數或複數
• dst表示輸出影象
• flags表示轉換標記
• nonzeroRows表示要處理的dst行數，其餘行的內容未定義（請參閱dft描述中的卷積示例）

 　　完整程式碼如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 讀取影象
img = cv2.imread('irving.jpg', )
# 影象進行灰度化處理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅立葉變換
# cv2.DFT_COMPLEX_OUTPUT 執行一維或二維複數陣列的逆變換，結果通常是相同大小的複數陣列
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 將頻譜低頻從左上角移動到中心位置
dft_shift = np.fft.fftshift(dft)
# 頻譜影象雙通道複數轉換為0~255區間
result = 10 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 傅立葉逆變換
ishift = np.fft.ifftshift(dft_shift)
iimg = cv2.idft(ishift)
iresult = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])


# 顯示影象
plt.subplot(131), plt.imshow(img, cmap='gray')
plt.title('Input image')
plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(result, cmap='gray')
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(iresult, cmap='gray')
plt.title('inverse Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()

 　　結果如圖所示：

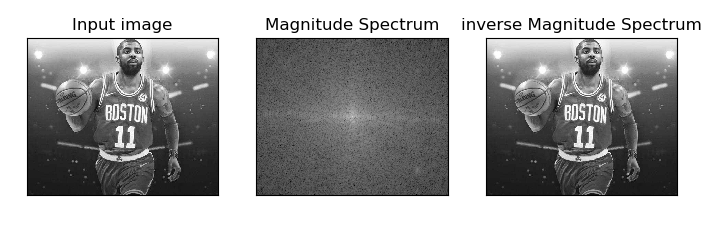
 　　傅立葉變換的目的並不是為了觀察影象的頻率分佈（至少不是最終目的），更多情況下是為了對頻率進行過濾，通過修改頻率以達到影象增強，影象去噪，邊緣檢測，特徵提取，壓縮加密等目的。

　　過濾的方法一般有三種：低通（low-pass），高通（high-pass），帶通（band-pass），下面一一學習。

5，高通濾波

　　高通濾波器是指通過高頻的濾波器，衰減低頻而通過高頻，常用於增強尖銳的細節，但會導致影象的對比度會降低。該濾波器將檢測影象的某個區域，根據畫素與周圍畫素的差值來提升畫素的亮度。下圖展示了“Lena”圖對應的頻譜影象，其中心區域為低頻部分。

　　接著通過高通濾波器覆蓋掉中心低頻部分，將255的點變換為0，同時保留高頻部分，其處理過程如下圖所示：

　　高通濾波器主要通過矩陣設定構造，其核心程式碼如下：

rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

　　下面自己百度找一張lena圖，做一下，程式碼如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取影象
img = cv2.imread('lena.jpg', 0)

# 傅立葉變換
fimg = np.fft.fft2(img)
fshift = np.fft.fftshift(fimg)

# 設定高通濾波器
rows, cols = img.shape
crow, ccol = int(rows/2), int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

# 傅立葉逆變換
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)

# 顯示原始影象和高通濾波處理影象
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('gray Image')
plt.axis('off')
plt.subplot(122), plt.imshow(iimg, 'gray'), plt.title('Result Image')
plt.axis('off')
plt.show()

 　　結果如下：

 　　左邊圖為lena的灰度圖，右邊圖為高通濾波器提取的邊緣輪廓影象，它通過傅立葉變換轉換為頻譜影象，再將中心的低頻部分設定為0，再通過傅立葉逆變換轉換為最終輸出影象。

6，低通濾波

　　所謂低通就是保留影象中的低頻成分，過濾高頻成分，可以把過濾器想象成一張漁網，想要低通過濾器，就是要將高頻區域的訊號全部拉黑，而低頻區域全部保留。例如，在一幅大草原的影象中，低頻對應著廣袤且顏色趨於一致的草原，表示影象變換緩慢的灰度分量；高頻對應著草原影象中的老虎等邊緣資訊，表示影象變換較快的灰度分量，由於灰度尖銳過度造成。

　　低通濾波器是指通過低頻的濾波器，衰減高頻而通過低頻，常用於模糊影象。低頻濾波器與高通濾波器相反，當一個畫素與周圍畫素的插值小於一個特定值時，平滑該畫素的亮度，常用於去噪和模糊化處理。如PS軟體中的高斯模糊，就是常見的模糊濾波器之一，屬於削弱高頻訊號的低通濾波器。

　　下圖展示了lena圖對應的頻譜影象，其中心區域為低頻部分。如果構造低通濾波器，則將頻譜影象中心低頻部分保留，其他部分替換為黑色0，其處理過程如圖所示，最終得到的效果圖為模糊影象。

　　那麼，如何構造該濾波影象呢？如下圖所示，濾波影象是通過低通濾波器和頻譜影象形成。其中低通濾波器中心區域為白色255，其他區域為黑色0。

　　低通濾波器主要通過矩陣設定構造，其核心程式碼如下：

rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

 　　通過低通濾波器將模糊影象的完整程式碼如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 讀取影象
img = cv2.imread('lena.jpg', 0)

# 傅立葉變換
# fimg = np.fft.fft2(img)
fimg = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
fshift = np.fft.fftshift(fimg)

# 設定低通濾波器
rows, cols = img.shape
# 中心位置
crow, ccol = int(rows / 2), int(cols / 2)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

# 掩膜影象和頻譜影象乘積
f = fshift * mask
print(f.shape, fshift.shape, mask.shape)
# (199, 198, 2) (199, 198, 2) (199, 198, 2)


# 傅立葉逆變換
ishift = np.fft.ifftshift(f)
iimg = cv2.idft(ishift)
iimg = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])

# 顯示原始影象和高通濾波處理影象
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('gray Image')
plt.axis('off')
plt.subplot(122), plt.imshow(iimg, 'gray'), plt.title('Result Image')
plt.axis('off')
plt.show()

　　結果如下：

參考文獻：https://blog.csdn.net/Eastmount/article/details/89474405

https://blog.csdn.net/Eastmount/article/details/89645301

Python + OpenCV影象處理課程（https://study.163.com/course/courseLearn.htm?courseId=1005317018#/learn/text?lessonId=1052508042&courseId=1005317018）

https://www.cnblogs.com/tenderwx/p/5245859.html

https://blog.csdn.net/u013921430/article/details/79934162?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_p