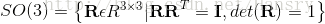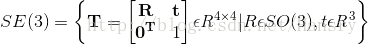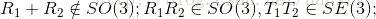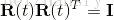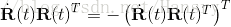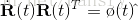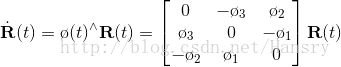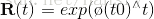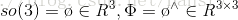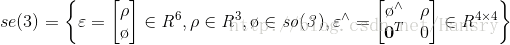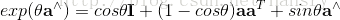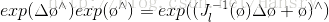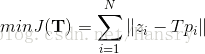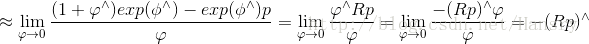SLAM學習——李群與李代數
轉自:https://blog.csdn.net/hansry/article/details/74905673
1.李群與李代數基礎
三維旋轉矩陣構成特殊正交群SO(3),而變換矩陣構成了特殊歐氏群SE(3):
其中特殊正交群SO(3)和特殊歐氏群SE(3),對加法不封閉,而對乘法封閉。則有:
群,是一種集合加上一種運算的代數結構,主要滿足有:封閉性、結合律、么元、逆等性質。而李群,則是指具有連續光滑性質的群。
對於李代數,考慮任意旋轉矩陣 R,會隨著時間變化而變化,即為時間的函式:R(t)。
則有:
通過對其時間的求導,可得到一個等式:
其中 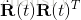
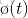
由於 R 為正交矩陣,則有
我們可以看到,每對旋轉矩陣求一次導,只需左乘一個上述矩陣即可,設 to=0,且R(0)=I,通過一階泰勒展開解上述微分方程,可以得到:
該方程說明了旋轉矩陣R通過一個反對稱矩陣通過指數關係發生了聯絡。
對於李代數而言,在不引起歧義的情況下,我們可以說李代數的元素是上述所提到的向量和反對稱矩陣,而李代數so(3),(注意這裡與SO(3)不同),則元素為三維向量和三維反對稱矩陣,而se(3)的元素是六維向量和六維反對稱矩陣,其表達方式為:
對於se(3)裡面的p的三維向量,代表的是平移,但是含義與變換矩陣中的平移是不同的,這點需要特別注意,另外在se(3)李代數中,符號“ ^“僅僅表示向量到反對稱矩陣,而是廣泛的表達為從”向量到矩陣“。
2.指數與對數對映
上面我們提到了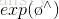
其中,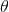
 中,那麼李群和李代數就是一一對應的了。
中,那麼李群和李代數就是一一對應的了。
3.李代數求導與擾動模型
為什麼要使用李代數呢?使用李代數的一大動機是用來進行優化,因為在從空間點到觀測資料的轉換時,總會有噪音的存在,優化機器人的位姿使得噪聲最小。
對某個旋轉矩陣R,對應的李代數為 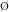
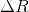
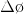
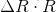
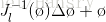
而對於se(3)李代數而言,同樣有類似的性質。
對於李代數求導問題,在SLAM中,我們要估計一個相機的位姿,該姿態是由李群上的SO(3)和SE(3)而來的。那麼,假設某時刻攝像機的位姿為T,觀察到了點 p,得到了觀測資料z,那麼有: z=Tp+w,其中w為觀測誤差。
為了使得實際值與觀測值最大程度的接近,那麼我們需要使噪聲最小,而這個即是優化的過程,通過對轉換矩陣 T 的求導,得到整體誤差的最小化:
為了求解這個問題,我們經常會構建與位姿有關的函式,然後討論該函式關於位姿的導數,以調整當前的估計值。因為變換矩陣只是單純的李群,對加法不封閉,於是我們可以轉換成李代數進行求導。因為李代數由向量組成,所以具有良好的加法運算。在求解李代數問題時,有倆種思路:
1.用李代數表示姿態,然後根據李代數加法來對李代數求導
2.對李群左乘或者右乘一個微小擾動,然後對該擾動求導,稱為左擾動模型和右擾動模型。第一種對應到李代數的求導模型,第二種對應到擾動模型。
李代數求導模型
關於李代數求導,考慮到SO(3),假設對一個空間點 p 進行了旋轉,得到了 Rp ,要計算旋轉後點的座標相對於旋轉的導數,有: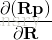
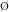
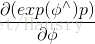
於是,按照導數的定義,我們可以有: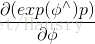
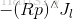
擾動模型(左乘)
在模型之前,有麥克勞林展開式有:
y=e^x運用麥克勞林展開式並捨棄餘項:e^x≈1+x+x^2/2!+x^3/3!+……+x^n/n!
接著上述問題,另一種求導方式為,對R進行一次擾動 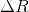
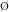
該式求導比上述簡單:
最終得到結果省去了計算一個雅克比矩陣,這使擾動模型更加有用!!其中,第二步到第三步運用了麥克勞林展開式,捨去了高次項。從第四步到第五步,可以將反對稱符號看做叉積,變換之後變號,從而求得結果!!
最後,這些模型的求解可以一個Sophus庫進行協助求解!!!