概率密度函式是概率論中的核心概念之一，用於描述連續型隨機變數所服從的概率分佈。在機器學習中，我們經常對樣本向量x的概率分佈進行建模，往往是連續型隨機變數。很多同學對於概率論中學習的這一抽象概念是模糊的。在今天的文章中，SIGAI將直觀的解釋概率密度函式的概念，幫你更深刻的理解它。

從隨機事件說起

回憶我們在學習概率論時的經歷，隨機事件是第一個核心的概念，它定義為可能發生也可能不發生的事件，因此是否發生具有隨機性。例如，拋一枚硬幣，可能正面朝上，也可能反面朝上，正面朝上或者反面朝上都是隨機事件。擲骰子，1到6這6種點數都可能朝上，每種點數朝上，都是隨機事件。

與每個隨機事件a關聯的有一個概率值，它表示該事件發生的可能性：p(a)這個概率值必須在0到1之間，22即滿足下面的不等式約束：

0<= p(a)<=1

另外，對於一次實驗中所有可能出現的結果，即所有可能的隨機事件，它們的概率之和必須為1：

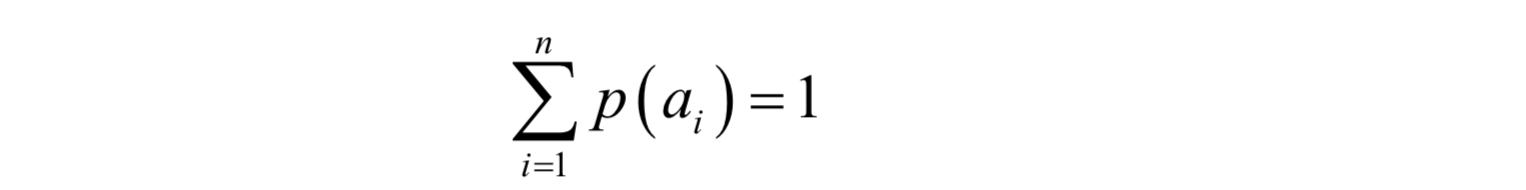
這些隨機事件不會同時發生，但必須有一件會發生。例如，對於拋硬幣，不是正面朝上就是反面朝上，不會出現其他情況（這裡假設硬幣丟擲去後不會立著），因此有：

p(正面朝上)+p(反面朝上)=1

很多時候，我們假設這些基本的隨機事件發生的概率都是相等的，因此，如果有n個基本的隨機事件，要使得它們發生的概率之和為1，則它們各自發生的概率都為：

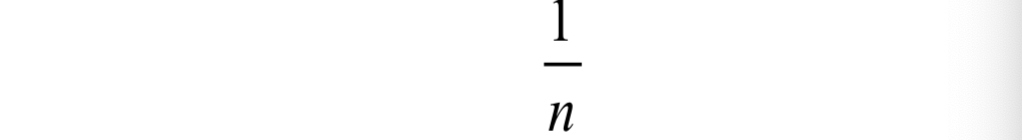
對於拋硬幣，正面朝上和反面朝上的概率各為1/2，對於擲骰子，每個點朝上的概率各為1/6。對於這種只有有限種可能的情況，我們通過列舉各種可能的情況，可以算出每個事件發生的概率。例如，如果我們要計算擲骰子出現1點或者2點的概率，只需要將這兩點至少有一點出現的情況數，比上所有可能的情況數，就得到概率值：

上面的例子中，隨機事件所有可能的情況只有有限種，而且可以用整數對這些隨機事件進行編號，如 。

然而，有有限就有無限，對於可能有無限種情況的隨機事件，我們該如何計算它發生的概率？考慮一個簡單的問題，有一個長度和高度都為1的正方形，如果我們隨機的扔一個點到這個正方形裡，這個點落在右上方也就是紅色區域裡的概率是多少？

你可能已經想到了，直接用紅色三角形的面積，比上整個正方形的面積，應該就是這個概率：

在這裡，隨機點所落的位置座標(x, y)的分量x和y都是[0, 1]區間內的實數，這有無限多種情況，不能再像之前那樣把所有的情況全部列出來，統計出這些情況的數量，然後和總情況數相除得到概率值。而是使用了“面積”這一指標來計算。看來，對這種型別的隨機事件，我們得藉助於“長度”，“面積”，“體積”這樣的積分值來計算。

如果用集合來描述這些隨機事件的話，第一種情況是有限集，我們可以給集合裡的每個元素編號。第二種情況是無限集，元素的個數多到無法用整數下標來編號。

整數集與實數集

高中時我們學過集合的概念，並且知道整數集是z，實數集是R。對於有限集，可以統計集合中元素的數量即集合的基數（cardinal number，也稱為集合的勢cardinality）。對於無限集，元素的個數顯然是無窮大，但是，都是無窮大，能不能分個三六九等呢？

回憶微積分中的極限，對於下面的極限：

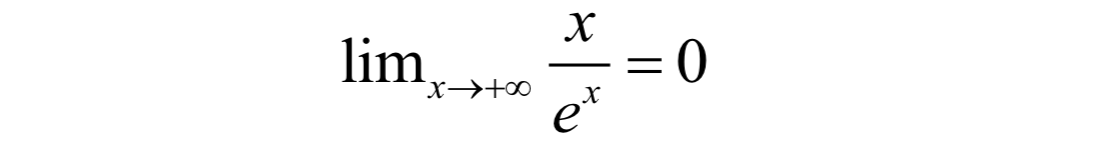
雖然當x趨向於正無窮的時候，x和exp(x)都是無窮大，但它們是有級別的，在exp(x)面前，x是小巫見老巫。

同樣的，對於整數集和實數集，也是有級別大小的。任意兩個整數之間，如1與2之間，都密密麻麻的分佈著無窮多個實數，而且，只要兩個實數不相等，不管它們之間有多靠近，如0.0000001和0.0000002，在它們之間還有無窮多個實數。在數軸上，整數是離散的，而實數則是連續的，密密麻麻的佈滿整個數軸。因此，實數集的元素個數顯然比整數要高一個級別。

隨機變數

變數是我們再熟悉不過的概念，它是指一個變化的量，可以取各種不同的值。隨機變數可以看做是關聯了概率值的變數，即變數取每個值有一定的概率。例如，你買彩票，最後的中獎金額x就是一個隨機變數，它的取值有3種情況，以0.9的概率中0元，0.09的概率中100元，0.01的概率中1000元。變數的取值來自一個集合，可以是有限集，也可以是無限集。對於無限集，可以是離散的，也可以是連續的，前者對應於整數集，後者對應於實數集。

離散型隨機變數

隨機變數是取值有多種可能並且取每個值都有一個概率的變數。它分為離散型和連續型兩種，離散型隨機變數的取值為有限個或者無限可列個（整數集是典型的無限可列），連續型隨機變數的取值為無限不可列個（實數集是典型的無限不可列）。

描述離散型隨機變數的概率分佈的工具是概率分佈表，它由隨機變數取每個值的概率p(x = xi )= pi依次排列組成。它滿足：

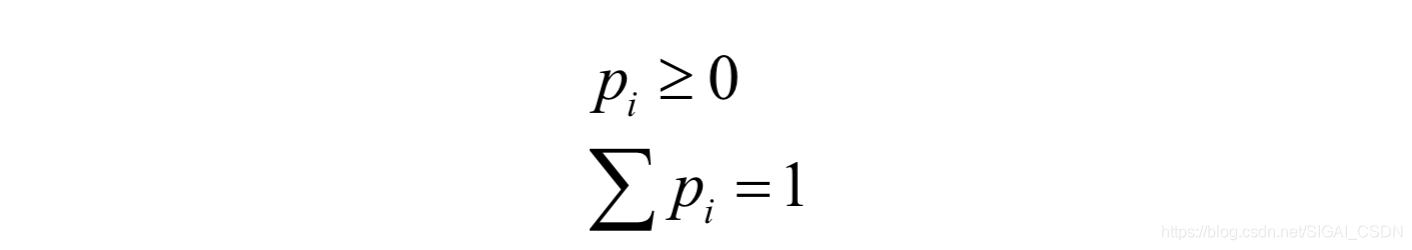
下面是一個概率分佈表的例子：

表2.2 一個隨機變數的概率分佈表

如果我們把前面例子中擲骰子的點數x看做是隨機變數，則其取值為1-6之間的整數，取每個值的概率為1/6，這是典型的離散型隨機變數。

連續型隨機變數

把分佈表推廣到無限情況，就可以得到連續型隨機變數的概率密度函式。此時，隨機變數取每個具體的值的概率為0，但在落在每一點處的概率是有相對大小的，描述這個概念的，就是概率密度函式。你可以把這個想象成一個實心物體，在每一點處質量為0，但是有密度，即有相對質量大小。

以上面在正方形內隨機扔一個點的問題為例，此時，落點的座標(x, y)就是連續型隨機變數，落到任意一點(x, y)的概率值為0。因為這一個點的數量為1，而整個正方形內的點數為無窮大，二者之比值為0：

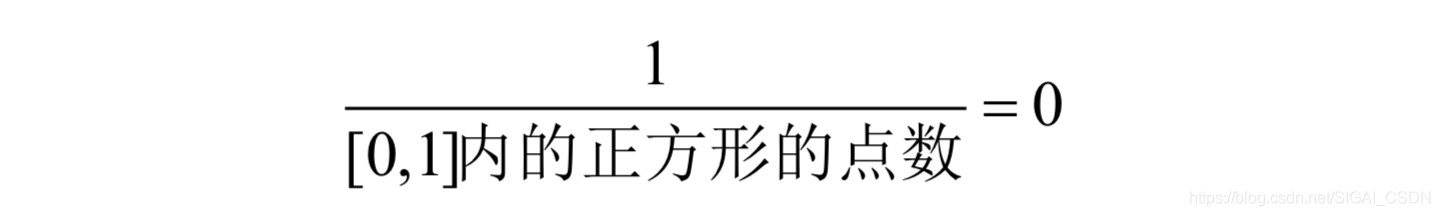
這實際上是均勻分佈，即落在任何一點處的概率值相等。對於有些問題，落在各個不同的點處的概率是不相等的，就像一個實心物體，有些點處的密度大，有些點處的密度小，由此引入了概率密度函式的概念。

一個函式如果滿足如下條件，則可以稱為概率密度函式：

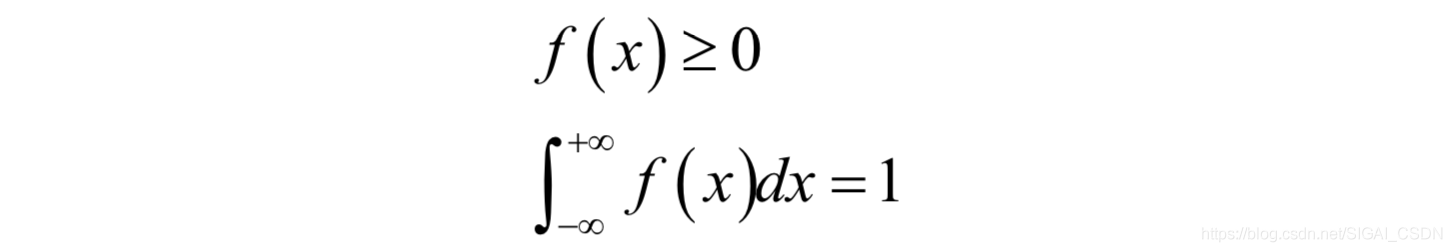
這可以看做是離散型隨機變數的推廣，積分值為1對應於取各個值的概率之和為1。分佈函式是概率密度函式的變上限積分，它定義為：

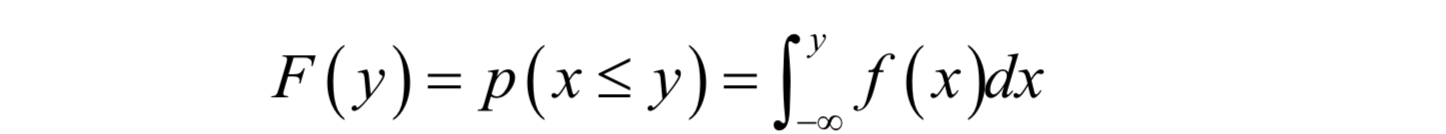
顯然這個函式是增函式，而且其最大值為1。分佈函式的意義是隨機變數的概率。注意，連續型隨機變數取某一個值的概率為0，但是其取值落在某一個區間的值可以不為0：

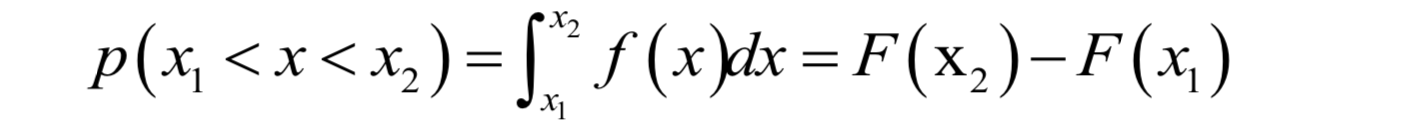
雖然連續型隨機變數取一個值的概率為0，但取各個不通過的值的概率還是有相對大小的，這個相對大小就是概率密度函式。這就好比一個物體，在任意一點處的質量為0，但在這一點有密度值，密度值衡量了在各點處的質量的相對大小。

從這個角度，我們可以將概率密度函式解釋為隨機變數落在一個區間內的概率與這個區間大小的比值在區間大小趨向於0時的極限：

這個過程如下圖所示：

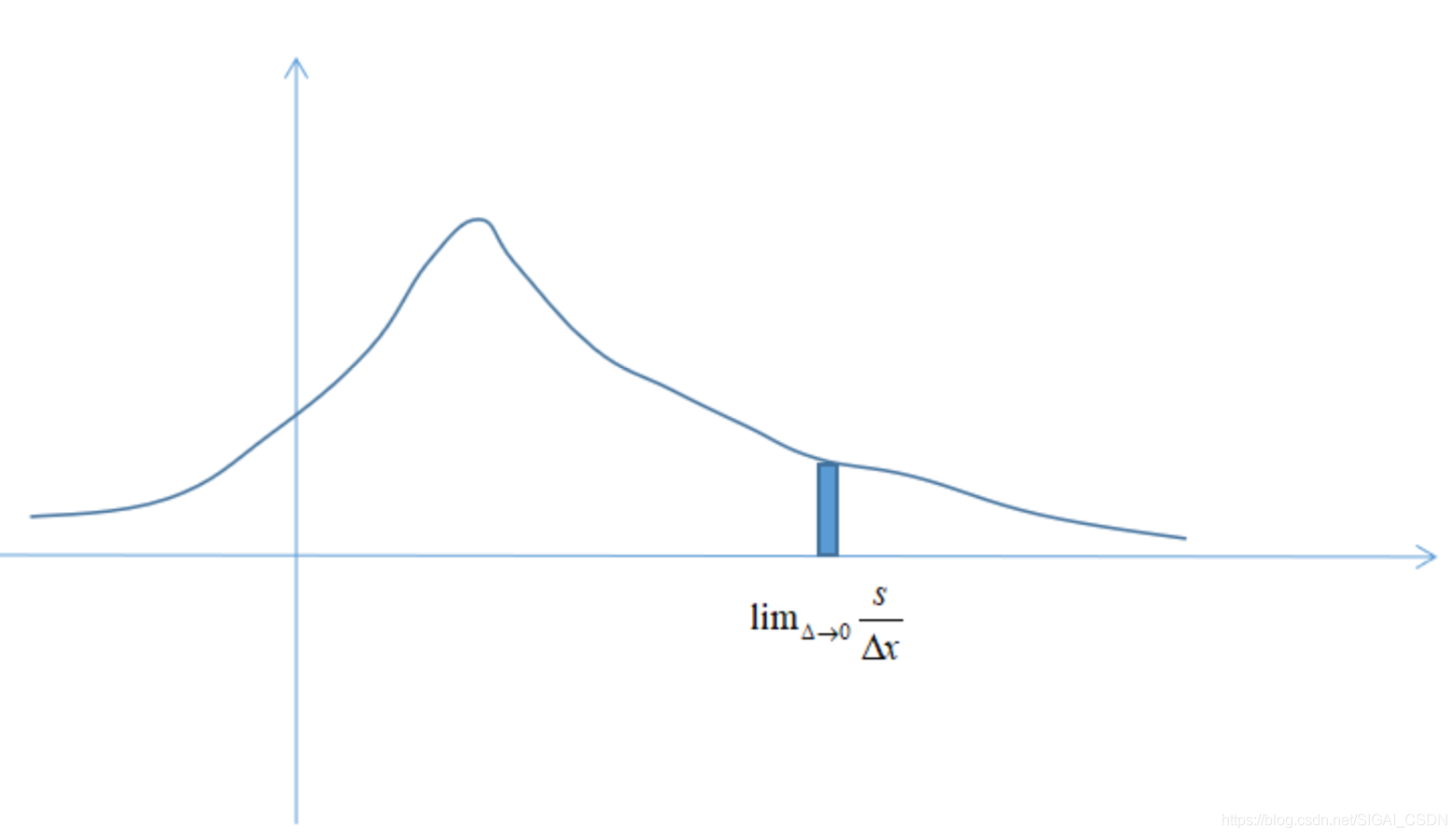
還是以上面的正方形為例，如果要計算隨機點(x, y)都落在區間[0, 0.5]內的概率，可以這樣計算：

這個面積，就是積分值，對應於分佈函式。最常見的連續型概率分佈是正態分佈，也稱為高斯分佈。它的概率密度函式為：

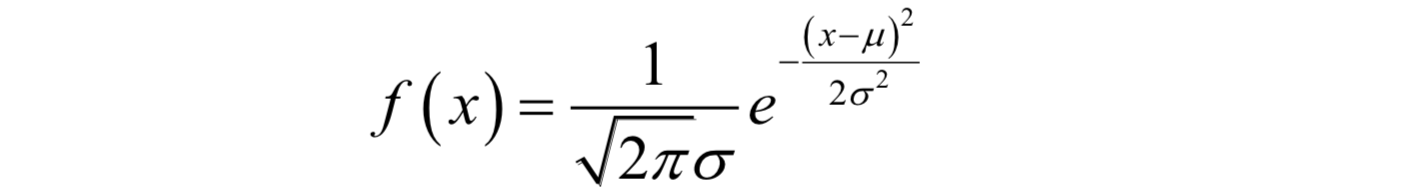
其中μ和 分別為均值和方差。現實世界中的很多資料，例如人的身高、體重、壽命等都近似服從正態分佈。另外一種常用的分佈是均勻分佈，如果隨機變數x服從區間[a,b]內的均勻分佈，則其概率密度函式為：

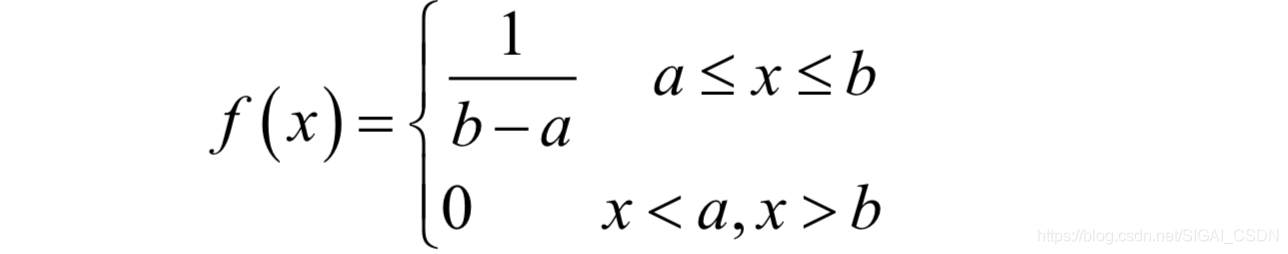
在程式設計和機器學習中，這兩種分佈是最為常見的。