OpenCV 中的傅立葉變換

  OpenCV 中相應的函式是 cv2.dft() 和 cv2.idft()。和前面輸出的結果一樣，但是是雙通道的。第一個通道是結果的實數部分，第二個通道是結果的虛數部分。輸入影象要首先轉換成 np.float32 格式。我們來看看如何操作。 
  在前面的部分我們實現了一個 HPF（高通濾波），後面做 LPF（低通濾波）將高頻部分去除。其實就是對影象進行模糊操作。首先我們需要構建一個掩模，與低頻區域對應的地方設定為 1, 與高頻區域對應的地方設定為 0。

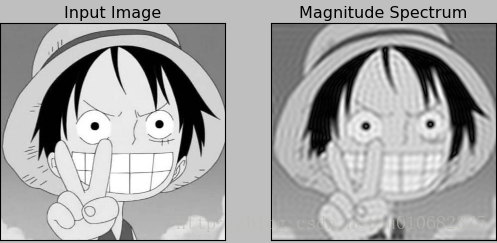
import cv2
import numpy as np 
from matplotlib import pyplot as plt 

img = cv2.imread('image/lufei.jpeg',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
rows,cols = img.shape
crow,ccol = rows/2,cols/2
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30,ccol-30:ccol+30] = 1
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0], img_back[:,:,1])

plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Input Image'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(img_back,cmap = 'gray')
plt.title('Magnitude Spectrum'),plt.xticks([]),plt.yticks([])
plt.show()
 

結果圖： 

         
OpenCV 中的函式 cv2.dft() 和 cv2.idft() 要比 Numpy 快。但是Numpy 函式更加使用者友好。

DFT 的效能優化

  當陣列的大小為某些值時 DFT 的效能會更好，當陣列的大小是 2 的指數時 DFT 效率最高。當陣列的大小是 2， 3， 5 的倍數時效率也會很高。所以如果你想提高程式碼的執行效率時，你可以修改輸入影象的大小（補 0）。對於OpenCV 你必須自己手動補 0，但是 Numpy，你只需要指定 FFT 運算的大小，它會自動補 0。那我們怎樣確定最佳大小呢？OpenCV 提供了一個函式:cv2.getOptimalDFTSize()，可以同時被 cv2.dft() 和 np.fft.fft2() 使用。
 

為什麼拉普拉斯運算元是高通濾波器

為什麼拉普拉斯運算元是高通濾波器？為什麼 Sobel 是 HPF？等等。對於第一個問題的答案我們以傅立葉變換的形式給出。我們一起來對不同的運算元進行傅立葉變換並分析它們

import cv2
import numpy as np 
from matplotlib import pyplot as plt 

mean_filter = np.ones((3,3))
x = cv2.getGaussianKernel(5,10)
gaussian = x*x.T

scharr = np.array([[-3,0,3],[-10,0,10],[-3,0,3]])
sobel_x = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
sobel_y = np.array([[-1,-2,-1],[0,0,0],[1,2,1]])
laplacian = np.array([[0,1,0],[1,-4,1],[0,1,0]])

filters = [mean_filter,gaussian,laplacian,sobel_x,sobel_y,scharr]
filter_name = ['mean_filter','gaussian','laplacian','sobel_x','sobel_y','scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]

for i in xrange(6):
    plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
    plt.title(filter_name[i]),plt.xticks([]),plt.yticks([])
plt.show()
 

結果圖： 
           
  從影象中我們就可以看出每一個運算元允許通過那些訊號。從這些資訊中我 
們就可以知道那些是 HPF 那是 LPF. 

傅立葉結果重排後的對稱性