決定寫這樣一篇文章對我自己而言是個極大的挑戰，如此抽象的概念，對於高中磁場都沒怎麼的我，誒!

雖然考研還未涉及場這個概念，但是其主要的載體梯度，散度，旋度，那時從來都不缺席的，所以這也是一塊重要的知識！本著知識完整性的角度，我希望你能迎難而上，盡力而為吧！將做過的題總結總結，是你寫本篇文章的目的！

需要討論：

1.梯度場

2.散度場

3.旋度場

4.有勢場，保守場，無旋場

寫在前：重點不是去寫具體的計算怎麼算，我希望你能夠從巨集觀角度進行把握

首先是場的概念：若對全空間或其中某一區域V中每一點M，都有一個數量或者向量與之對應，則稱在V上給定了一個數量場或者向量場。

M的位置可以由座標確定，故對於數量場，等於總是給定了一個數量函式u(x,y,z)

                                              對於向量場，等於總是給定了一個向量函式u（x,y,z）=P(x,y,z)i +Q(x,y,z)j +R(x,y,z)k

1.梯度場

運算的物件是數量，運算的結果是向量

從上面分析可知，梯度場是一個向量場，因為梯度是方向導數最大值的方向。

舉例子來說，現在有一座山，山的陡峭程度程度是不一樣的，那麼經過梯度的運算，山上的每一點都會形成一個向量，它告訴你：在這個點處最陡的方向是哪個方向，而向量的大小則代表了這個最陡的方向到底有多陡。

2.散度場

散度的運算物件是向量，運算的結果是數量

故散度場是一個數量場

如果現在我們考慮在任何一個點(或者說這個點的周圍極小的一塊區域)，在這個點上，向量場的發散程度，如果是正的，代表這些向量場是往外散出的。如果是負的，代表這些向量場是往內集中的。

舉例來說，我們知道，黑洞可以吸收它周圍的一切物質，包括光線，這時，所以的一切都往這中心匯聚，此時散度值為負。

而如果一個恆興不斷塌縮最終變成爆炸變成超新星的過程中，物質都離中間而去，此時散度值為正。

3.旋度場

旋度的運算物件是向量，運算的結果也是向量。

表示曲線，流體等旋轉程度的量，

想象這是大海中的旋渦，考慮現在它有多大的可能想把船給掀翻，也不知道理解對不對。

4.有勢場，保守場，無旋場

在這裡還需要附上一個求勢函式的方法：

（1）首先判斷是有勢場

（2）根據P Q R與u（x,y,z）關於偏導數的關係列式子求解，這裡就是之前平面與路徑無關理論中求原函式的方法！

以例題說明。

例1：source：1000題chapter6

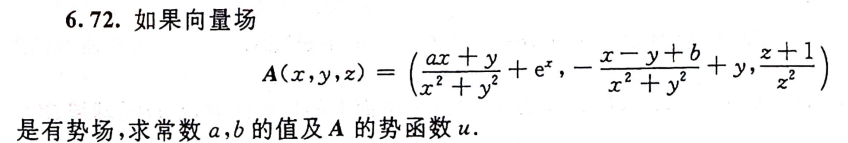
分析：有勢場說明旋度為0，就可以計算出a,b

勢函式就是求原函式，此處用的是湊的手法，有點技巧性，需多做題積累！

總結：對於不熟悉的知識，不要恐懼，你會發現，計算還是蠻簡單的是不是？？