動畫相關理論詳解

一 、骨架

骨架由一系列具有層次關係的關節（骨骼）和關節鏈組成，是一種樹結構，選擇其中一個是根關節，其它關節是根關節的子孫，可以通過平移和旋轉根關節移動並確定整個骨架在世界空間中的位置和方向。父關節運動能影響子關節運動，但子關節運動對父關節不產生影響，因此，平移或旋轉父關節時，也會同時平移或旋轉其所有子關節。

二、骨骼的表示

通常會將關節進行編號\(0\sim N-1\),編號也稱關節索引，通過索引查詢關節比關節名查詢高效的多。通常一個關節包含以下資訊

• 關節名
• 父關節索引（根關節的父關節索引為-1，為無效索引）
• 關節繫結姿勢的逆變換矩陣（offset矩陣）

所謂繫結姿勢，是指蒙皮網格頂點繫結至骨骼時，關節的位置、朝向、及縮放，通常會儲存關節變換的逆矩陣。

struct Joint
{
    Matrix4x4 m_inverseBindPose;
    const char* m_name;
    U8 m_iParent;
};

struct Skeleton
{
    U32 m_jointCount; // 關節數
    Joint* m_aJoint;  // 關節陣列
};

三、姿勢

把關節旋轉、平移、縮放，就能為骨架擺出各種姿勢，關節的姿勢被定義為關節相對於某座標系的位置、朝向、縮放。通常骨架存在繫結姿勢、區域性姿勢、全域性姿勢。

3.1 繫結姿勢

繫結姿勢是網格繫結到骨骼之前的姿勢，也就是講網格當作正常、沒有蒙皮、完全不涉及骨骼三角形網格來渲染的姿勢，通常是設計師繫結模型時預設的。如下面的左圖就是一個繫結姿勢，右圖是任意一個姿勢。

3.2 區域性姿勢

區域性姿勢是關節相對於父關節來指定的，是一種常見的姿勢。區域性姿勢儲存為\(TQS\)的格式，表示相對與父關節的位置、朝向、縮放,根關節的父節點可以認為是世界座標系原點。

關節在三維軟體裡通常是顯示成一個點或者一個球，實際上，每個關節定義了一個座標空間。在數學上，關節姿勢就是一個仿射變換，用\(P_j\)表示關節\(j\)代表的仿射變換，它是一個\(4\times 4\)

struct JointPose
{
    Quaternion m_rot; // 相對父關節朝向
    Vector3 m_trans;  // 在父關節中的座標
    Vector3 m_scale;  // 相對父關節的縮放
};

區域性關節姿勢矩陣\(P_j\)作用到以關節\(j\)座標系表示的點或者向量時，其結果是將點或者向量變換到父關節座標空間表示的點。

3.3 全域性姿勢

全域性姿勢是相對於區域性姿勢而言的，它是關節相對於模型空間或者世界空間的姿勢（區域性姿勢是相對於父關節的姿勢）。試想一下，我們如何將關節\(j\)座標空間的點\(q\)表示成全域性座標（世界座標）呢？通過前面的介紹，我們知道\(P_jq\)將得到\(q\)在\(j\)父節點空間中的座標，如此，可以通過從該關節開始一直遍歷到根關節，即可將\(q\)變換到世界座標系中表示的座標形式。

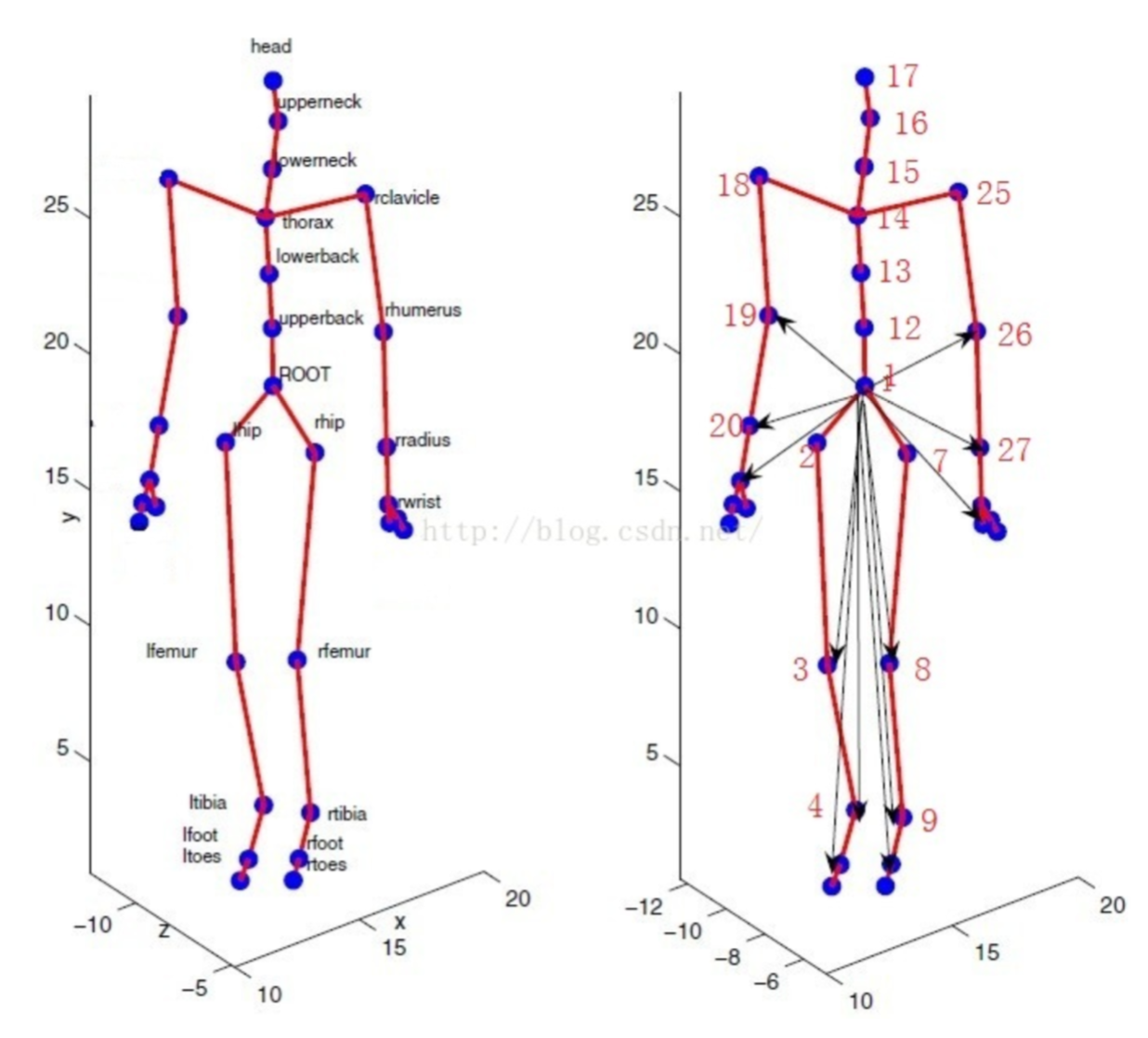
如上圖，左邊是人體骨架名稱，右邊是對應的標號，root的編號為1，現在假我們將關節rfemur空間的點\(q\)變換到世界座標系中,rfemur關節編號是8，我們用\(P_8\)表示它的區域性姿勢矩陣，以此類推，那麼\(q\)在世界座標系中的座標可以表示為
\[ q' = P_1P_7P_8q \]
對應的變換矩陣是\(P_1P_7P_8\),該變換矩陣便是關節8的全域性姿勢矩陣，也就是前面說的那樣，它直接將關節8座標系下的點變換到世界座標系中。我們知道，變換矩陣的逆表示逆變換，全域性姿勢矩陣的逆矩陣可以將世界空間的點變換到關節空間中，如上面的例子
\[ q=(P_1P_7P_8)^{-1}q' \]
我們稱\((P_1P_7P_8)^{-1}\)矩陣為Offset矩陣，這個矩陣很關鍵，有必要強調它的含義：Offset矩陣將全域性空間（世界空間）點變換到關節的區域性空間中，是全域性姿勢矩陣的逆矩陣，它在模型繫結後一直保持不變。另外，還有一個比較重要的矩陣是GlobalTransform矩陣（也叫Combine矩陣），這個矩陣與Offset做的事情恰好相反，它是將關節空間的點變換到全域性空間，那它不就是全域性姿勢矩陣嘛？當然不是，前面說過，這些叫xx姿勢矩陣的是針對繫結姿勢而言的，繫結的姿勢是唯一的，當動畫播放時，模型會存在一個實時姿勢，這個GlobalTransform矩陣正是將實時姿勢下的關節空間點變換到世界空間中。接下來還有一個矩陣就是骨架的最終變換矩陣FinalTransform矩陣（也稱蒙皮矩陣，後面會解釋），這個矩陣表示了骨架最終的變換，他們的關係是
\[ F= G O \]
上面\(F,G,O\)分別是FinalTransform矩陣、GlobalTransform矩陣、Offset矩陣的簡寫。上面說的\(F\)與\(G\)矩陣的作用恰好相反，那是不是\(F\)就成了單位矩陣了呢？其實不是的，再次強調，O矩陣是固定的，但是\(G\)矩陣是實時姿勢矩陣，因為當骨架運動時關節姿勢變了\(G\)就會變了。既然這樣，那麼\(G\)矩陣如何計算呢？用\(P_j'\)表示動畫播放時關節\(j\)的實時姿勢，還是用上面的例子
\[ G_8=P_1'P_7'P_8' \]
這樣關節8的蒙皮矩陣就是
\[ F_8=G_8O_8=P_1'P_7'P_8'(P_1P_7P_8)^{-1} \]

四、蒙皮原理

所謂蒙皮就是計算骨架在某一狀態下網格頂點的位置。每個頂點可以繫結到一個至多個骨骼（unity裡面是最多4個），動畫播放時，頂點隨著關節運動，頂點的最終變換就等於它所繫結的骨架變換的加權和。對於每個頂點，我們需要有以下資訊

• 該頂點繫結到的骨骼索引
• 該頂點的每個繫結骨骼的權重，他表示了骨架對頂點的影響力。

加權平均的計算時，頂點繫結的所有骨架的權重和為1。通常設每個頂點最多繫結到4個骨架，程式儲存如下

struct SkinnedVertex
{
    float m_position[3]; // 頂點位置（x,y,z）
    float m_normal[3];   // 頂點法向量 （Nx,Ny,Nz）
    float m_u, m_v;      // 紋理座標
    U8 m_jointIndex[4];  // 關節的索引
    float m_jointWeight[4]; // 關節權重
};

上面提到過蒙皮矩陣，但是還沒正式定義，蒙皮矩陣就是把頂點從繫結姿勢變換到骨骼的當前姿勢的矩陣。蒙皮矩陣和前面的基變更矩陣不同，它只是把頂點變換到新的位置，頂點變換前後都在世界空間中（或模型空間中）。和上面一樣用\(F_j\)表示關節\(j\)的蒙皮矩陣，假設某個頂點\(v\)受到上面關節14、18、15、25的影響，對應點權重分別為\(w_1,w_2,w_3,w_4\)，則頂點\(v\)的最終變換位置為
\[ v'=w_1F_{14}v+w_2F_{18}v+w_3F_{15}v+w_4F_{25}v \]

上面公式就是頂點的蒙皮計算方法。實際上，在記憶體中，一般儲存關節的兩個矩陣，一個是區域性姿勢矩陣\(P_j\)（也可以叫節點矩陣，Node矩陣），一個是全域性姿勢的逆矩陣Offset矩陣，通過前面的知識我們知道，其實Offset矩陣可以通過區域性姿勢矩陣計算得到，為什麼我們還要存一個呢？因為Offset矩陣用的非常頻繁，每次使用都去計算一次沒有必要，世界開銷略大。

蒙皮矩陣的計算過程可以理解為先將點通過Offset矩陣變換到關節空間，再通過GlobalTransform矩陣變換到全域性空間。這裡需要提一點，unity和C++中儲存的模型頂點座標是一開始就確定的，動畫過程中不會變，也就是每一幀不會去更新頂點座標，只是會通過蒙皮計算得到頂點最終位置，然後渲染到螢幕上。

五、動畫混合

動畫混合指的是讓一個以上的動畫片段對角色最終姿勢起作用的技術，也即是將兩個或者多個輸入姿勢結合，產生骨骼的輸出姿勢。混合技術可以自動產生大量新動畫，而無須設計師手工繪製。例如現在有一個閉嘴動畫和張大嘴動畫，我們可以在這兩個動畫間進行一系列插值，這樣就可以得到從閉嘴到張大嘴的一系列動畫。線性插值是

常用的動畫混合技術，設某關節的兩個姿勢是\(P_a\)和\(P_b\),線性插值計算公式為
\[ P_{LERP}=(1-\beta)P_a+\beta P_b \]
其中\(\beta\)是混合因子，它的值介於\(0\sim1\)。對關節姿勢進行線性插值即為對\(4 \times 4\)變換矩陣插值，然而直接對矩陣插值是不行的，我們需要分別對\(TRS\)進行插值。

對\(T\)進行插值很簡單，直接使用普通的線性插值（\(T\)是平移向量）
\[ T_{LERP}=(1-\beta)T_a+\beta T_b \]
旋轉部分需要使用四元數插值（球面線性插值），假設我們需要在兩個單位四元數之間插值，從\(q_a\)到\(q_b\), 如下圖

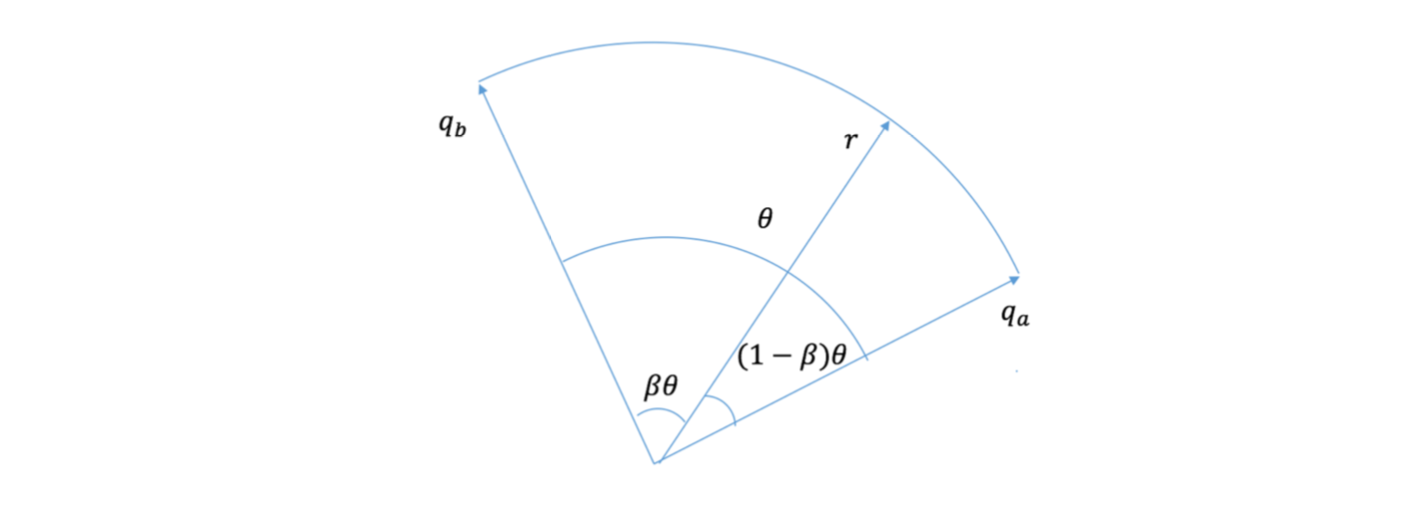
根據四元數的運算性質,我們的插值公式為
\[ r=A(\theta)q_a+B(\theta)q_b \tag{1} \]
我們的目的是求出\(A(\theta)\)和\(B(\theta)\),在(1)兩邊點乘\(q_b\),得
\[ q_b \cdot r=A(\theta)q_b\cdot q_a+ B(\theta)q_b\cdot q_b \tag{2} \]
化簡後即
\[ cos(\beta\theta)=A(\theta)cos(\theta)+B(\theta) \tag{3} \]
同樣的，兩邊點乘\(q_a\)化簡得
\[ cos((1-\beta)\theta)=A(\theta)+B(\theta)cos(\theta) \tag{4} \]
綜合\((3),(4)\)得
\[ A(\theta)=\frac{sin((1-\beta)\theta)}{sin(\theta)} \\ B(\theta) = \frac{sin(\beta \theta)}{sin(\theta)} \quad \quad \; \]
代入\(A(\theta)、B(\theta)\)從而得到四元數插值公式。