Python假設檢驗
阿新 • • 發佈:2018-12-12
import pandas as pd import pylab import math import numpy as np import matplotlib.pyplot as plt %matplotlib inline from scipy.stats import norm import scipy.stats import warnings warnings.filterwarnings("ignore") df=pd.read_csv("http://ww2.amstat.org/publications/jse/datasets/normtemp.dat.txt",sep=" ",names=['Temperature','Gender','Heart Rate']) df.head()
| Temperature | Gender | Heart Rate | |
|---|---|---|---|
| 0 | 96.3 | 1 | 70 |
| 1 | 96.7 | 1 | 71 |
| 2 | 96.9 | 1 | 74 |
| 3 | 97.0 | 1 | 80 |
| 4 | 97.1 | 1 | 73 |
df.describe()| Temperature | Gender | Heart Rate | |
|---|---|---|---|
| count | 130.000000 | 130.000000 | 130.000000 |
| mean | 98.249231 | 1.500000 | 73.761538 |
| std | 0.733183 | 0.501934 | 7.062077 |
| min | 96.300000 | 1.000000 | 57.000000 |
| 25% | 97.800000 | 1.000000 | 69.000000 |
| 50% | 98.300000 | 1.500000 | 74.000000 |
| 75% | 98.700000 | 2.000000 | 79.000000 |
| max | 100.800000 | 2.000000 | 89.000000 |
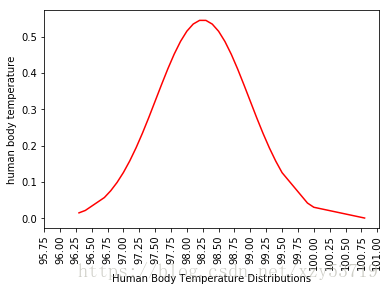
#假設檢驗 #前提檢驗正態分佈 observed_temperatures = df['Temperature'].sort_values() bin_val = np.arange(start = observed_temperatures.min(),stop=observed_temperatures.max(),step=50) mu,std = np.mean(observed_temperatures),np.std(observed_temperatures) p = norm.pdf(observed_temperatures, mu,std) plt.hist(observed_temperatures,bins=bin_val,normed=True,stacked=True) plt.plot(observed_temperatures,p,color='r') plt.xticks(np.arange(95.75,101.25,0.25),rotation=90) plt.xlabel('Human Body Temperature Distributions') plt.ylabel('human body temperature') plt.show() print("Average (Mu):"+str(mu)+"/ Standard Deviation:" + str(std))
Average (Mu):98.24923076923076/ Standard Deviation:0.7303577789050376
#確定指標進行正態檢驗
x = observed_temperatures
shapiro_test,shapiro_p = scipy.stats.shapiro(x)
print("Shapiro-Wilk Stat:",shapiro_test,"Shapiro-Wilk p-Value:",shapiro_p)
k2,p = scipy.stats.normaltest(observed_temperatures)
print("k2:",k2,"p:",p)
#以上兩種方法,p值大於0.05,認為正態分佈
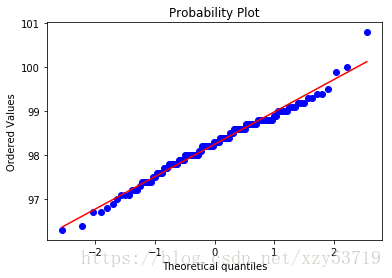
#Another method to determining normality is through Quantile-Quantile Plots
#QQ圖檢查正態分佈
scipy.stats.probplot(observed_temperatures,dist='norm',plot=pylab)
pylab.show()Shapiro-Wilk Stat: 0.9865769743919373 Shapiro-Wilk p-Value: 0.2331680953502655 k2: 2.703801433319236 p: 0.2587479863488212
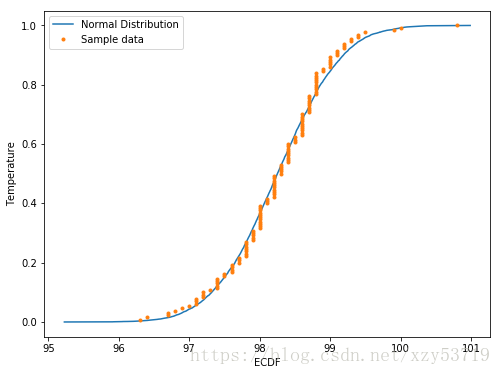
#另一種檢測正態分佈的方法
def ecdf(data):
#Compute ECDF
n = len(data)
x = np.sort(data)
y = np.arange(1,n+1) / n
return x,y
# Compute empirical mean and standard deviation
#Number of samples
n = len(df['Temperature'])
#Sample mean
mu = np.mean(df['Temperature'])
#Sample standard deviation
std = np.std(df['Temperature'])
print("Mean Temperature:",mu,"Standard deviation:",std)
#基於當前的均值和標準差,隨機生成一個正態分佈
normalized_sample = np.random.normal(mu,std,size=10000)
normalized_x,normalized_y = ecdf(normalized_sample)
x_temperature,y_temperature = ecdf(df['Temperature'])
#Plot the ECDFs
fig = plt.figure(figsize=(8,6))
plt.plot(normalized_x,normalized_y)
plt.plot(x_temperature,y_temperature,marker='.',linestyle='none')
plt.xlabel('ECDF')
plt.ylabel("Temperature")
plt.legend(("Normal Distribution","Sample data"))Mean Temperature: 98.24923076923076 Standard deviation: 0.730357778905038
Out[73]:
<matplotlib.legend.Legend at 0xb3437b8>
#驗證98.6為平均溫度
from scipy import stats
CW_mu = 98.6
stats.ttest_1samp(df['Temperature'],CW_mu,axis=0)
#T-Stat -5.454 p-value 近乎0,拒絕原假設Ttest_1sampResult(statistic=-5.454823292364077, pvalue=2.410632041561008e-07)
#檢驗男女體溫是否明顯區別
#兩獨立樣本t檢驗
#H0:兩樣本沒有明顯差異,H1:有明顯差異
female_temperature = df.Temperature[df.Gender==2]
male_temperature = df.Temperature[df.Gender==1]
mean_female_temperature = female_temperature.mean()
mean_male_temperature = male_temperature.mean()
print("男體溫均值:",mean_male_temperature,"女體溫均值:",mean_female_temperature)
#兩獨立樣本t檢驗
stats.ttest_ind(female_temperature,male_temperature,axis=0)
#由於p值0.024 < 0.05 ,拒絕原假設,我們有95%的自信度認為是有差異的男體溫均值: 98.1046153846154 女體溫均值: 98.39384615384616
Ttest_indResult(statistic=2.2854345381654984, pvalue=0.02393188312240236)