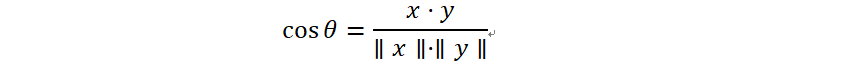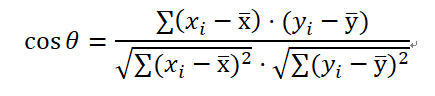說明

一直想總結一下以前讀過的一片文章來概括一下自己對矩陣的重新認識。首先說明一下這篇文章是《神奇的矩陣》建議大家有空可以去讀一下原文這是一片很不錯的文章。作者洋洋灑灑的講述了矩陣背後的意義，讓我對矩陣的認識上升了一個臺階。在此感謝作者！我在這裡只是對自己所學的總結。相信大家讀完之後一定能夠明白一些矩陣的核心概念背後的物理意義。

空間

首先說空間的特質就是可以容納運動，這裡的運動更加準確的來說就是一種躍遷、變換。我們可以想象在波爾的原子模型中環繞原子核的電子在吸收或者是釋放能量之後直接從這個軌道一下子變換到另一個軌道這個場景。進一步，線性空間就是就是可以容納線性變換的集合。

這裡說到了集合，那麼對於執行緒空間的它是誰的集合呢？是向量。向量不像是我們最基本認識的最直觀的向量一個有方向的有向線段，這裡的向量更加的一般化是一串有序的數。首先來說這裡的方向更加一般化不像我們直觀的體會到的上下左右，東西南北，而是某一個物體的某一個方面。比如大小，顏色，重量這些都是向量中的方向。而量就是它們在數值上的體現比如大象3立方米，顏色紅色，重量7千克。這樣一個向量就可以描述一個人，一個教室乃至萬事萬物。

那麼如何在空間中確定一個向量呢？就是設立一組座標系（也就是基）。這裡的座標系其實就是一些線性不相關的向量。就像三維空間中的基就是三個互相垂直的軸。線上性空間中只要找到幾個線性不相關的向量就可以表示其它任何的向量。比如在二維平面上我們一旦找到兩個相交的向量我們就能夠表示其它任何一個二維向量。當然當我們需要表示一個n維的物體的時候我們就需要找到n個不相關的向量。在一個線性空間中一個向量就是其中的一個點，或者是點到座標原點的帶有方向的線段。同時我們也就知道一個由多個線性不相關的向量組成的矩陣就可以描述一個線性空間的座標系。厲害吧！: - )

矩陣與變換

在這裡引出一個問題，如何描述一個向量線上性空間中的運動或者是變換？其實這就是矩陣的作用，線上性空間中選定基之後向量描述物件，矩陣刻畫物件的運動用矩陣與向量的乘法來描述運動。這裡的運動可以理解為伸縮和旋轉因為平移之後的向量還是同一個向量。

β = Mα中M就描述了α向量到β向量的運動。

B = MA中M就描述了一組向量{a}到{B}的運動。

由上面可以看出矩陣充當了很多的角色這裡澄清一下：

①  矩陣是座標系？座標系是由一堆的線性無關的向量所構成的只不過在這裡是用矩陣的形式來表示。

②  矩陣是運動的描述？是的。

③  總的來說如果一個矩陣單獨出現那麼它就描述了一個座標系。如果它與一個向量或者是矩陣相乘的時候那麼它就描述了一個變換。

矩陣與方程組

方程組的解之與係數有關，所以把係數提取出來放在一起也就成了矩陣。矩陣的行變換也就是解方程時的加減消元的過程。

方程組Ax = b的意義，方程組有解有兩種解釋。

①  空間幾何圖形有公共的交點（線，面，超平面）。

②  這說明b這個向量能夠用A的列向量表示，所以說明b這個向量在A的列向量所構成的空間裡。比如說A = [a1,a2,…an]，方程組就是x1a1 + x2a2 + …+xnan = b。這裡會發生一個相容就是在一個高維空間裡放一個低維度的向量是完全ok的。這時A的秩與[Ab]的秩是一樣的（矩陣的秩表示向量構成空間的維數）。

矩陣的基與座標

首先宣告我們討論的矩陣是非奇異的（不是滿秩的矩陣）。

假設{a}{b}是兩組同一空間中的不同的基，如果有一個矩陣M使得{b} = {a}M那麼我們就說M實現了從基{a}到基{b}的一個轉換。於是我們得到右乘一個矩陣就是將一組基轉換到另一組基。矩陣又一次表示了運動，左乘表示物件的變換，右乘表示座標的變換。這也就是我們想起了相對運動，固定座標系下的一個物件的變換相當於固定物件下的座標系的變換。

接著上面的例子，假設{a}對應的座標是x，{b}對應的座標是y那麼則有Y = M-1X。左乘一個矩陣就是將一組基中的下標變成另一組基下的下標。由此可見By = Ax 就是說x經過A的變換和y經過B的變換相等就說明了y與x最後經過變換成為了同一個東西。既然是同一個東西我們就可以這樣理解有一個向量在A的基下表達為x在B的基下表達為y！而這時我們就可以把這些向量左邊乘上矩陣的這種形式看成是一種身份的識別！如Ax是在說有一個向量在A的基下表示為x在B的基下表示為y但是他們本身是同一個向量。實在是震撼！（這裡的左乘與前面所說的矩陣表示運動的觀點不矛盾）

特殊的矩陣

矩陣的連乘表示變換的疊加，而變換又可以分解為旋轉與拉伸。對應到的矩陣就是旋轉對應的是旋轉矩陣，拉伸對應的是對角矩陣。順便說一句旋轉矩陣有對角矩陣的性質，它是一種對角矩陣。對於旋轉矩陣的連乘我們可以看作是把一個向量沿著多個方向的疊加。對於對角矩陣來的連乘來說就是對向量放大或縮小的疊加。而普通矩陣連乘就是旋轉與伸縮的疊加。

矩陣的等價與相似

矩陣的等價於相似都是為了簡化計算。首先說矩陣的等價。定義上來說存在可逆矩陣P和Q使得PAQ = B我們就說A和B等價。假設A就是一個M×N的矩陣，dim = {M,N}我們就可以說A是dim的一個子空間，而在變換的過程中可逆就是可以變換出去然後在變換回來既然已經可逆了那麼就說明了這個變換是不改變矩陣維度的。於是我們得到了A和B的維度相同也就是A和B的秩相同。也就是他們代表了同一個維度的子空間，從可觀測和可控制的角度來看他們擁有相同的控制維數。這就是等價矩陣的意義。

上述的等價運算是一種簡化運算的方式，而相似變換的也可以達到簡化運算的效果。首先給出結論：相似矩陣就是同一個線性變換在不同基下的描述。也就是現在有一個變換如果選取座標系1這個變換就用A來表示，如果選擇座標系2就用B來表示。但事實上他們描述的是同一個變換。從定義來看存在可逆矩陣P滿足B = P-1AP我們就說B和A是可逆矩陣。在前面的描述中我們知道同一個空間可以由不同的座標系來描述而且他們的座標有對應的關係。假設現在我們選取的兩個座標系是[α][β]則有[β] = [α]P，那麼一個座標的對應關係就是x2 = P-1x1。

假設下標為1的基為[α]下標為2的基為[β]，從x到y的變化為T。則有x1經過T1得到y1，x2經過T2得到y2。我們已經知道[α][β]之間是有關係的那麼T之間又怎樣的關係呢？x2 = P-1x1再加上T2的轉換就成了y2了，在y2的基礎上加一個P的轉換就得到了y1了整個過程為PT2P-1X= y1。它與T1X1 = y1是一樣的。於是就得到了T2=P-1T1P。這也就是相似矩陣的定義T1與T2為相似矩陣，原來一族矩陣就是同一個線性變換的描述。

矩陣的相似對角化

特徵向量

如果存在一個矩陣它對一個向量只發生伸縮變換而不發生旋轉效果那麼我們稱這個向量就是這個矩陣的特徵向量。這這個矩陣對向量的作用只是伸縮，這樣我們的公式看起來就變得有意義多了Ax = λx。通過式子我們也能夠看到特徵向量不是一個向量而是一個向量族同時這個向量組線性相關。

對角化矩陣

對角化矩陣的目標是簡化運算。對角化的意思就是能夠找到一組基使得A變成一個對角矩陣那麼原來有關A的矩陣運算就變成了一個對角矩陣的運算（通過前面的描述我們可以知道A與這個對角矩陣是相似的，即同一個東西在不同座標系下的表示）。對角矩陣給了我們一個簡單的角度這種感覺就像是在機器學習中的特徵轉換一樣一個二維的曲線可以分割的資料有可能被一個三維的超平面線性分割；一個樣本空間中的隨機變數的分佈有可能看不出什麼特點來但是這個隨機變數的函式有可能有非常好的規律性；那麼一個矩陣在一個空間中的其中一個座標系下面表現的非常複雜但是在另一個座標系下就變得異常簡單。

矩陣A對角化的條件就是在這個n維空間中能夠找到n個線性不相關的特徵向量。當我們找到特徵向量的時候這n個特徵向量就能夠組成一個基然後去表示這個矩陣。求出特徵向量再求出特徵值我們就能夠將有關A與它的特徵向量的運算變成數乘運算。得到的矩陣的特徵值就是變化的幅度，而特徵向量就是變化的方向。

特徵值分解

也稱之為譜分解，這裡這說明物理意義。一個具有良好效能的矩陣分解成多個作用的疊加，特徵值和譜的乘積就代表了它對這個矩陣的貢獻，貢獻越大權重越大也就越重要。這個和PCA（主成成分分析）有相似的地方，主成成分分析就是將一個複雜的東西（函式，影象，音訊等）分解成若干等分，然後留下主要的部分去掉次要的部分。同樣的，多項泰勒展開也的階數越高那麼他的權重也就越低，所以平常我們只取一階、二階來代替全部的式子從而抓住主要的特性。奇異值分解也是這樣的原則。

內積與相關

內積可以衡量兩個函式的線性相似度（注意是線性相似度！）。它能夠代表兩個向量之間的夾角，為了消去長度帶來的影響我們通常使用餘弦相似度。

當然現實中通常會出現y = ax + b的形式這樣的話就會給上面的式子帶來麻煩，對應的策略就是讓每一個x和y都減去他們對飲的期望值然後在帶入上式計算，這也就是著名的皮爾遜相關係數。

行列式

行列式有兩種意義

①  行列式就是行列式中行或者列構成的“平行多面體”的有向體積。如果將一個行列式對應的矩陣對角化那麼就很好理解了。

將行列式矩陣對角化之後就將原來的不規則的多面體變成一個規則的多面體了，它的體積是。它真的是表示幾何體的體積！那麼原來不規則的體積與現在規則的體積的差別在哪裡？②他們之間相差一個座標變換矩陣的行列式。這也就是第二種解釋面積或體積的伸縮因子。行列式是有正有負的但是面積和體積都是正數，所以就有了行列式中的面積和體積的正負代表的是一個方向。比如說xyz都相反的互為映象。

到此我的感想輸出完畢，感謝《神奇的矩陣》作者！