洛谷傳送門

題目描述

司令部的將軍們打算在$N*M$的網格地圖上部署他們的炮兵部隊。一個$N*M$的地圖由$N$行$M$列組成，地圖的每一格可能是山地（用H 表示），也可能是平原（用P表示），如下圖。在每一格平原地形上最多可以佈置一支炮兵部隊（山地上不能夠部署炮兵部隊）；一支炮兵部隊在地圖上的攻擊範圍如圖中黑色區域所示：

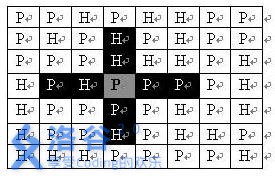
如果在地圖中的灰色所標識的平原上部署一支炮兵部隊，則圖中的黑色的網格表示它能夠攻擊到的區域：沿橫向左右各兩格，沿縱向上下各兩格。圖上其它白色網格均攻擊不到。從圖上可見炮兵的攻擊範圍不受地形的影響。 現在，將軍們規劃如何部署炮兵部隊，在防止誤傷的前提下（保證任何兩支炮兵部隊之間不能互相攻擊，即任何一支炮兵部隊都不在其他支炮兵部隊的攻擊範圍內），在整個地圖區域內最多能夠擺放多少我軍的炮兵部隊。

輸入輸出格式

輸入格式：

第一行包含兩個由空格分割開的正整數，分別表示$N$和$M$；

接下來的$N$行，每一行含有連續的$M$個字元（P或者H），中間沒有空格。按順序表示地圖中每一行的資料。$N≤100$；$M≤10$。

輸出格式：

僅一行，包含一個整數K，表示最多能擺放的炮兵部隊的數量。

輸入輸出樣例

輸入樣例#1：

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

輸出樣例#1：

6

解題分析

如果直接暴力列舉前兩行的狀態轉移， 複雜度是$O(m\times 2^{3n})$的， 會$TLE+MLE$。所以預處理一下合法狀態即可。（發現最多才60種…）

程式碼如下：

#include <cstdio>
#include <cctype>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
#define R register
#define IN inline
#define W while
#define MX 105
int n, m, ct;
int stat[65], sum[65], dp[105][65][65];
int mp[105];
char buf[15]
 
;
template <class T> IN T max(T a, T b) {return a > b ? a : b;}
void pre()
{
	int bd = (1 << m) - 1;
	for (R int i = 0; i <= bd; ++i)
	if((!((i << 1) & i)) && (!((i << 2) & i)))
	{
		++ct, stat[ct] = i, sum[ct] = __builtin_popcount(i);
		if(!(stat[ct] & mp[1])) dp[1][1][ct] = sum[ct];
	}
}
int main(void)
{
	R int i, j, k, cur;
	scanf("%d%d", &n, &m);
	for (i = 1; i <= n; ++i)
	{
		scanf("%s", buf);
		for (j = 0; j < m; ++j) if(buf[j] == 'H') mp[i] += 1 << j;
	}
	pre();
	for (i = 2; i <= n; ++i)
	{
		for (cur = 1; cur <= ct; ++cur)
		{
			if(!(mp[i] & stat[cur]))
			{
				for (j = 1; j <= ct; ++j)
				{
					if(!(stat[cur] & stat[j]))
					{
						for (k = 1; k <= ct; ++k)
						if((!(stat[cur] & stat[k])) && (!(stat[j] & stat[k])))
						dp[i][k][cur] = max(dp[i][k][cur], dp[i - 1][j][k] + sum[cur]);
					}
				}
			}
		}
	}
	int ans = 0;
	for (i = 1; i <= ct; ++i) for (j = 1; j <= ct; ++j) ans = max(ans, dp[n][i][j]);
	printf("%d", ans);
}