OpenGL投影矩陣
目錄
綜述
電腦螢幕是2D表面,必須將OpenGL渲染的3D場景作為2D影象投影到計算機螢幕上,所以就需要用到投影變換。首先,將所有頂點資料從眼睛座標轉換為裁剪座標。然後,這些裁剪座標的各分量(x,y,z)通過除以w分量被變換到規範化座標(NDC)。所以其實做了兩步操作:
- 將相機空間座標變換到投影空間
- 將投影空間座標變換到NDC空間
因此,我們必須記住裁剪(視錐體剔除)和NDC變換都整合到了變換中,下面的章節描述了怎樣從left、right、bottom、top、near、far這6個引數構造投影矩陣。需要注意的是視錐裁剪是在各個分量(、、)除以之前完成的。、、通過與作比較,如果任何裁剪空間座標比小,或者比大這個座標都將會被丟棄。
然後,OpenGL將重繪發生剪下的多邊形邊緣(如下圖所示)。
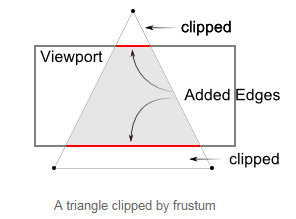
透視投影
在透視投影中,一個3D點在從金字塔平截頭視錐體空間(相機空間)被對映到一個立方體空間(NDC);其各分量範圍被如下對映:
x: [l,r]->[-1,1]
y: [b,t]->[-1,1]
z: [-n,-f]->[-1,1]

注意,相機空間是在右手座標系中定義的,但是NDC使用的是左手座標系。也就是說,原點處的相機沿著相機空間中軸看,但是在NDC空間中它是看向軸的。由於**glFrustum()**的near和far引數只接受正數,所以我們需要在構造投影矩陣的時候讓Z軸反向。
在OpenGL中,一個在相機空間的3D點會被投影到近平面(投影平面)上。下圖展示瞭如何將相機空間中的點投影到近平面上。

從視錐體的頂檢視來看,相機空間的x座標,被對映到,其通過使用相似三角形的比率來計算,如下所示:
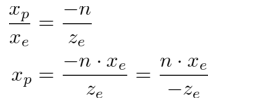
從視錐體的側檢視來看,也是類似的方式計算:
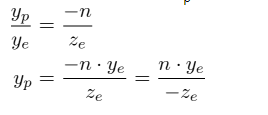
注意,取決於;他們與成反比。換句話說,他們都被除。這是構造投影矩陣的第一條線索。在通過乘以矩陣來變換眼睛座標系之後,裁剪座標仍然是齊次座標。它最終需要變為歸一化裝置座標(NDC),所以還需要除以裁剪座標的分量。
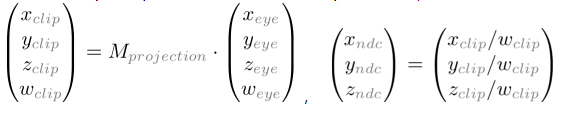
因此,我們可以將裁剪座標的分量設定為。並且,矩陣的第4行變為。
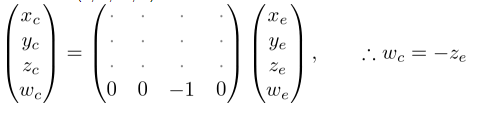
接下來,我們將和對映到具有線性關係的NDC空間的和:
[l,r]⇒[-1,1]
[b,t]⇒[-1,1]

然後,我們將、代入上述方程式。

注意,我們使每個方程都除以,以進行透視除法.我們之前將設定為,並且括號內術語變為裁剪座標系的和。
從這些方程式中,我們可以找到的第1行和第2行。
 現在,我們只有用第3行的來解決。與其他演算法略有不同,因為相機空間中的總是被投影到近平面上的。但是我們需要用於裁剪和深度測試的唯一值,並且在以後我們不會去逆變換深度值。由於我們知道z不依賴於x或y值,因此我們借用分量來找到和之間的關係,可以像下面這樣指定的第3行。
現在,我們只有用第3行的來解決。與其他演算法略有不同,因為相機空間中的總是被投影到近平面上的。但是我們需要用於裁剪和深度測試的唯一值,並且在以後我們不會去逆變換深度值。由於我們知道z不依賴於x或y值,因此我們借用分量來找到和之間的關係,可以像下面這樣指定的第3行。
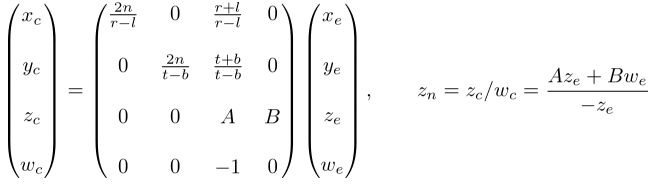 在相機空間中,因此等式變為:
為了找到係數A和B,我們使用的關係;和,並將它們放入上面的等式中。
在相機空間中,因此等式變為:
為了找到係數A和B,我們使用的關係;和,並將它們放入上面的等式中。
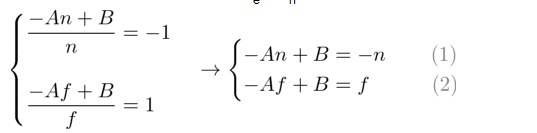 為了求解A和B的等式,重寫B的等式(1):
將方程(1’)代入方程(2)中的B,然後求解A:
為了求解A和B的等式,重寫B的等式(1):
將方程(1’)代入方程(2)中的B,然後求解A:
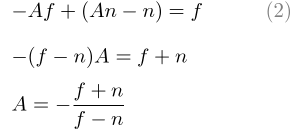 將A放入方程(1)中以找到B :
將A放入方程(1)中以找到B :

我們找到了A和B,因此和的變換如下:
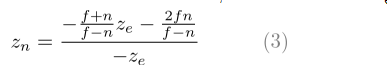 最終,我們找到了全部矩陣的元素,完成的矩陣如下所示:
最終,我們找到了全部矩陣的元素,完成的矩陣如下所示:
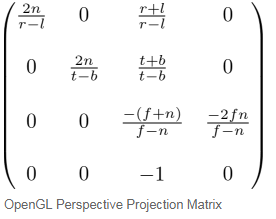 上述矩陣是通用的視錐體矩陣。如果視錐是對稱的(和),那麼它可以被簡化為如下矩陣:
上述矩陣是通用的視錐體矩陣。如果視錐是對稱的(和),那麼它可以被簡化為如下矩陣:

在離開之前,請再看一下等式(3)中
