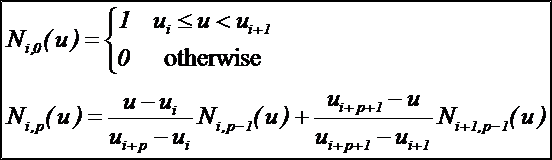B樣條基函式——B-Spline Basis Functions
B-Spline Basis Functions
摘要Abstract：直接根據B樣條的Cox-deBoor遞推定義寫出計算B樣條基函式的程式，並將計算結果在OpenSceneGraph中顯示。
關鍵字Key Words：B Spline Basis Functions、OpenSceneGraph
一、概述Overview
有很多方法可以用來定義B樣條基函式以及證明它的一些重要性質。例如，可以採用截尾冪函式的差商定義，開花定義，以及由de Boor和Cox等人提出的遞推公式等來定義。我們這裡採用的是遞推定義方法，因為這種方法在計算機實現中是最有效的。
令U={u0,u1,…,um}是一個單調不減的實數序列，即ui<=ui+1，i=0,1,…,m-1。其中，ui稱為節點，U稱為節點向量，用Ni,p(u)表示第i個p次B樣條基函式，其定義為：
B樣條基有如下性質：
a) 遞推性；
b) 區域性支承性；
c) 規範性；
d) 可微性；
二、程式 Codes
直接根據B樣條基函式的Cox-deBoor遞推定義，寫出計算B樣條基函式的程式如下：
標頭檔案BSplineBasisFunction.h：
/*
* Copyright (c) 2013 eryar All Rights Reserved.** File : BSplineBasisFunction.h* Author : [email protected]* Date : 2013-03-23 22:13** Description : Use Cox-deBoor formula to implemente the * B-Spline Basis functions.*
*/
#ifndef _BSPLINEBASISFUNCTION_H_#define _BSPLINEBASISFUNCTION_H_#include <vector>class BSplineBasisFunction{
public: BSplineBasisFunction(const std::vector<double ~BSplineBasisFunction(void);public:
/*
* @brief Binary search of the knot vector.
*/ int FindSpan(double u); /* * @brief * @param [in] i: span of the parameter u; * [in] p: degree; * [in] u: parameter; */ double EvalBasis(int i, int p, double u); /* * @breif Get knot vector size. */ int GetKnotVectorSize(void) const; /* * @breif Get the knot value of the given index. */ double GetKnot(int i) const;private: std::vector<double> mKnotVector;};#endif// _BSPLINEBASISFUNCTION_H_
實現檔案BSplineBasisFunction.cpp：
/** Copyright (c) 2013 eryar All Rights Reserved.** File : BSplineBasisFunction.cpp* Author : [email protected]* Date : 2013-03-23 22:14* Version : V1.0** Description : Use Cox-deBoor formula to implemente the * B-Spline Basis functions.**/#include "BSplineBasisFunction.h"BSplineBasisFunction::BSplineBasisFunction( const std::vector<double>& U ) :mKnotVector(U){}BSplineBasisFunction::~BSplineBasisFunction(void){}int BSplineBasisFunction::GetKnotVectorSize( void ) const{ return static_cast<int> (mKnotVector.size());}double BSplineBasisFunction::GetKnot( int i ) const{ return mKnotVector[i];}/** @brief Binary search of the knot vector.*/int BSplineBasisFunction::FindSpan( double u ){ int iSize = static_cast<int> (mKnotVector.size()); if (u >= mKnotVector[iSize-1]) { return iSize; } int iLow =0; int iHigh = iSize; int iMiddle = (iLow + iHigh) /2; while (u < mKnotVector[iMiddle] || u > mKnotVector[iMiddle+1]) { if (u < mKnotVector[iMiddle]) { iHigh = iMiddle; } else { iLow = iMiddle; } iMiddle = (iLow + iHigh) /2; } return iMiddle;}double BSplineBasisFunction::EvalBasis( int i, int p, double u ){ if ((i+p+1) >= GetKnotVectorSize()) { return0; } if (0== p) { if (u >= mKnotVector[i] && u < mKnotVector[i+1]) { return1; } else { return0; } } double dLeftUpper = u - mKnotVector[i]; double dLeftLower = mKnotVector[i+p] - mKnotVector[i]; double dLeftValue =0; double dRightUpper = mKnotVector[i+p+1] - u; double dRightLower = mKnotVector[i+p+1] - mKnotVector[i+1]; double dRightValue =0; if (dLeftUpper !=0&& dLeftLower !=0) { dLeftValue = (dLeftUpper / dLeftLower) * EvalBasis(i, p-1, u); } if (dRightUpper !=0&& dRightLower !=0)相關推薦
B樣條基函式——B-Spline Basis Functions
B-Spline Basis Functions 摘要Abstract：直接根據B樣條的Cox-deBoor遞推定義寫出計算B樣條基函式的程式，並將計算結果在OpenSceneGraph中顯示。 關鍵字Key Words：B Spline Basis Functions、OpenScene
B-spline Curves 學習之B樣條基函式的定義與性質（2）
轉自：http://www.cnblogs.com/icmzn/p/5100761.html B-spline Basis Functions:Definition 貝塞爾基函式用作權重。B-樣條基函式也一樣；但更復雜。但是它有兩條貝塞爾基函式所沒有的特性，即(1
B樣條曲線（B-spline Curves）
關鍵字：NURBS，基函式，控制點，節點， 看了網上很多相關資料才得以下筆，資料太多，這裡就不一一列舉了，感謝各位大佬的資料 本部落格順序不太好，看前面的東西可能需要提前看後面的東西。正在努力修煉，敬請諒解 寫了個B樣條曲線計算的完成程式，包括繪圖，https://
B-spline Curves 學習之B樣條曲線定義（4）
轉自：http://www.cnblogs.com/icmzn/p/5100789.html 給定 n + 1個控制點P0, P1, ..., Pn 和一個節點向量U = { u0, u1, ..., um }, p 次B-樣條曲線由這些控制點和節點向量U 定義
B-spline Curves 學習之B樣條曲線的移動控制點、修改節點分析（7）
轉自：http://www.cnblogs.com/icmzn/p/5101424.html B-樣條曲線：移動控制點 移動控制點是改變B-樣條曲線形狀的最明顯的方法。在前面頁討論的區域性修改方案說明了修改控制點 Pi 的位置僅影響在區間[ui, ui+p+1)
問題六十一：三次b樣條(b-spline)曲線的控制點和曲線形狀的對應——以迴旋體的“基本曲線”為例
在這一章節，我們以其中一段曲線段為例，改變其對應的控制點，看看曲線段形狀的改變，同時也看看對應的迴旋體圖形的改變。 控制點座標如下圖： “問題六十”中的“基本曲線”的控制點對應如上ABCDEF六個點（其中A點在1位置）。對應輸出的迴旋體圖形如下（再次貼出來）： 說
課堂筆記_ B樣條曲線和NUBRS
為什麼學習B樣條 Bezier曲線/曲面不支援區域性的修改和編輯； Bezier曲線/曲面拼接時，滿足幾何連續條件是十分困難的。 B樣條的歷史 1946年，Schoenberg提出了一種基於樣條的方法來近似曲線； B樣條的動機源於插值中的Ru
計算機圖形學--------充分理解B樣條曲線
樣條（spline）二字，從英文翻譯過來的，讓人費解。B樣條的數學定義更是讓人匪夷所思。看了好幾本參考教材，還是把總結一下B樣條這個概念。 一、解釋什麼是樣條。 實際應用中，樣條是一根富有彈性的細木條或塑料條。在應用CAD/CAM技術以前，航空、船舶和汽車製造業普遍採用手
B-樣條曲線：定義
其中 Ni,p(u)是 p次B-樣條基函式。 B-樣條曲線形式與貝塞爾曲線相似 。不像貝塞爾曲線, B-樣條曲線包含更多資訊，即：一系列的 n+1 個控制點， m+1個節點的節點向量，次數 p。 注意n, m 和 p必須滿足m = n + p + 1。更準確地，如果我們想要定義一個有 n + 1控制點的p次
[摘抄] Bezier曲線、B樣條和NURBS
Bezier曲線、B樣條和NURBS，NURBS是Non-Uniform Rational B-Splines的縮寫，都是根據控制點來生成曲線的，那麼他們有什麼區別了？簡單來說，就是: Bezier曲線中的每個控制點都會影響整個曲線的形狀，而B樣條中的控制點只會影響整個曲線的一部分，顯然B樣條提供了
OpenGL 繪制B樣條曲線
ember direction onexit cti target get 說明 spa glbegin http://blog.csdn.net/yangtrees/article/details/9026411 繪制B樣條曲線： #include <stdli
從零開始的openGL——四、紋理貼圖與n次B樣條曲線
前言 在上篇文章中，介紹瞭如何載入繪製模型以及滑鼠互動的實現，並且遺留了個問題，就是沒有模型表面沒有紋理，看起來很醜。這篇文章將介紹如何貼紋理，以及曲線的繪製。 紋理貼圖 紋理載入 既然是貼圖，那首先我們得要有合適的紋理圖片，openGL中支援的圖片為bmp格式。在這裡我還用到了個額外的庫glaux，但當時在
【 MATLAB 】MATLAB 實現模擬訊號取樣後的重建（三）應用三次樣條函式spline實現內插
前三篇博文講了三種方法進行內插重建訊號： 這篇文章使用三次樣條函式spline來實現內插重建，並分析重建誤差。 採用的案例依然是上篇博文中的案例： 模擬訊號： 對該訊號使用兩種不
樣條函式（spline function）—— 分段多項式函式（piecewise polynomial function）
1. 分段多項式函式 樣條函式是某種意義上的分段函式。 最簡單的樣條函式是一種分段多項式函式（piecewise polynomial function），樣條函式 S:[a,b]→R。
【HDOJ5528】Count a * b（積性函式）
題意：設f(i)為0<=x,y<=i-1且xy%i=0的(x,y)對數，g(i)為sigma f(j) [i%j==0] 給定n，求g(n)，答案對2^64取模 T<=2e4，n<=1e9 思路：這題堅定了我要找一個專業數學手的決心…… x,y從[0,i-1]等價於從[1,i]
薄板樣條插值---TPS(Thin Plate Spline)
薄板樣條插值—TPS(Thin Plate Spline) 插值 已知一系列的觀測點 ( x
（光滑樣條）Smoothing spline的數學推導
Smoothing spline的數學推導 參考斯坦福統計學習原理 光滑樣條的精髓在於在原本的擬合誤差的基礎上加了一個λ∫{f′′(t)}2dt\lambda\int\left\{f^{''}(t)\right\}^{2}dt
徑向基-薄板樣條插值數學公式、原理，以及程式碼實現基本過程
徑向基插值部分 徑向基函式RBF (Radial Basis Function)有以下五種基函式 其中r代表代待求點X與已知點Xi之間的向量距離 上邊的公式是適用於以上五種基函式的計算公式，其中X代表向量，不是一個數字 對於薄板樣條插值，其公式（是經過上邊
ThinkPHP單字母函式整理 A函式 B函式 C函式 D函式 F函式 L函式 R函式 S函式 U函式
有人不太喜歡TP這種單字母函式，其實這也是TP的一個特色，如果理解了這些函式的作用，不管是背，還是寫，都是非常方便的，接下來我們以字母順序開始。 A函式（基本是Action的簡寫） A函式是用來例項化我們的Action類的，例如我們的程式有2個Action分別是Inde
藍橋 鹼基 java b組 國賽
鹼基 生物學家正在對n個物種進行研究。 其中第i個物種的DNA序列為s[i]，其中的第j個鹼基為s[i][j],鹼基一定是A、T、G、C之一。 生物學家想找到這些生物中一部分生物的一些共性，他們現在關注那些至少在m個生物中出現的 長度為k的連續鹼基序列。準確的說，科學家關心的序