巴什博奕基礎情形

只有一堆n個物品，兩個人輪流從這堆物品中取物，規定每次至少取一個，最多取m個。最後取光者得勝。

如果n = m + 1； 我們假設第一個人拿走了k個， 還剩下 m + 1 - k。 因為1<=（m + 1 - k）<= m, 所以， 剩下的部分一定可以被第二個人一次性取走。

現在我們將上述規律加一推廣：
如果n=（m+1）r+s（r∈ N，s<= m)；
那麼先取者要拿走s個物品，如果後取者拿走k（k<= m)個，那麼先取者再拿走m+1-k個，結果剩下（m+1）（r-1）個，
以後保持這樣的取法，那麼先取者肯定獲勝

那麼在我方取最優解

現在我們換一個角度來考慮這個問題：
如果物品數量隨機，那麼先手一方勝利的概率是m/(m+1)，後手方勝利的概率是1/(m+1)

對於上述的問題， 我們可以用mod的方法快速的求出答案（其實三種博弈的最優美之處就是能用 %^&這三個符號完美解答）

`

巴什博弈演變

硬幣問題1

Alice和Bob在玩這樣的一個遊戲， 給定k個數組a1,a2,a3,……ak。 一開始， 有x枚硬幣， Alice和Bob輪流取硬幣， 每次所取硬幣的枚數硬頂要在 a1,a2,a3,……ak之中。 Alice先取， 取走最後一枚硬幣的一方獲勝。 當雙方都採取最優策略的時候， 誰會獲勝？ 題目假定a1,a2,a3,……ak之中一定有1。

下面我們來分情況討論到達自己時， 還有j枚硬幣的勝負情況：

1.題目規定， 取光所有的硬幣就獲勝， 這等價於輪到自己時如果沒有硬幣就失敗， 因此j = 0時是必敗態。
2.如果對於某個i（i<=i<= k）, 就j - ai是必敗態， 那麼j就是必勝態（如果當前有j枚硬幣， 只要取走ai枚對手就必敗→自己必勝）；
3.如果對於任意的i（1 <= i <= k）， j - ai都是必敗態的話， j就是必敗態（無論對手這麼走， 對手都必勝， 自己必敗）

根據這些規則， 我們都能利用動態規劃演算法按照j從小到大的順序計算必勝態。， 只要看x是必勝態還是必敗態， 我們就知道誰會取勝；

通常來說， 通過考慮每個小狀態的取勝條件， 判斷必勝條件和必勝態， 是有勝負的遊戲的基礎；

上程式碼

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

int x，k;
bool win[100000];
int a[100000];

void Bash()
{//輪到自己沒有硬幣則必敗；
    win[0] = false;

    for (int i = 1; i <= x; i++)
    {//如果可以讓對手達到必敗態， 則自己必勝；
        win[i] = false;
        for (int j = 0; j < k; i++)
            win[i] |= (a[j] <= i && !win[i - a[j]]); // |=   真真為真 真假為真  假假為假
    }
}

int main(void)
{
    while (scanf("%d %d", &x, &k) != EOF)
    {
        for (int i = 0; i < k; i++)
            scanf("%d", &a[i]);
        sort(a, a + k);
        memset(win, 0, sizeof(a));
        Bash();
        if (win[x])
            printf("Alicce!\n");
        else
            printf("Bob!\n");
    }
    return 0;
}

硬幣問題2

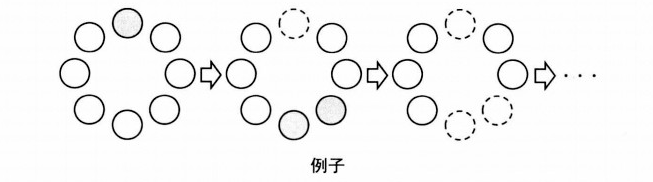
n枚硬幣排成一個圈。Alice和Bob輪流從中取一枚或者兩枚硬幣， 不過， 取兩枚時這兩枚必須是連續的。硬幣取走之後留下空位，想個空位的硬幣被認為是不連續。 A開始先取， 取走最後一枚硬幣的一方獲勝。雙方都採取最優策略的時候誰會取勝？

按照上面問題的想法， 我們來拆分一下問題；

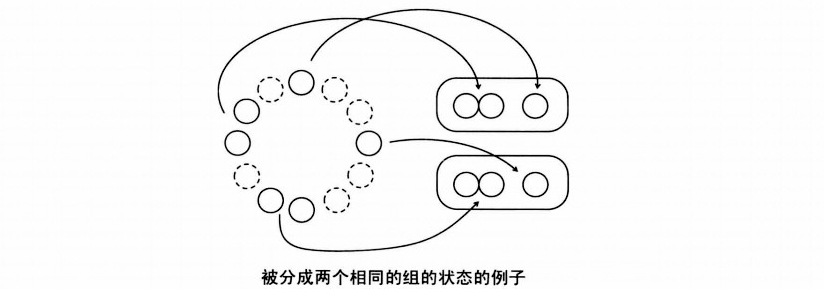
首先我們是想一下如下的情況。 將所有的剩餘硬幣分成完全相同的組別， 這個是必勝狀態還是必敗狀態？

事實上這是必敗態， 無論採取什麼策略， 對手只要在另一組中使用相同的策略， 就有回到了相同分組的狀態， 而最終的相同分組狀態就是（0，0）；

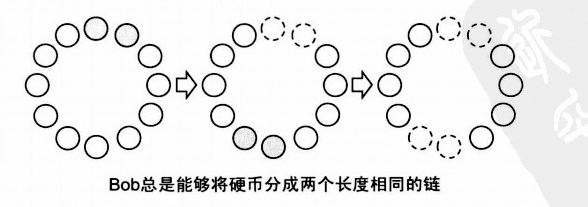
接下來， 我們迴歸正題。A在第一取走一枚或者兩枚硬幣之後，稱圈的硬幣就變成了長度為n - 1或者是n - 2 的。 Bob只要在中間位置根據鏈的奇偶性， 在鏈的中間位置取走1或者2枚， 就可以把所有的硬幣分成長度相同的兩個鏈。

正如我們所說的，這是必敗態， 也就是說， Alice必敗， Bob必勝，只不過， 當n <= 2， Alice可以一步取光， 所以勝利的是Alice， 除此之外， 在都進行最優解的情況下， Alice必敗。

int k;

if(k <= 2)
    printf("Alice!\n");
else
    printf("Bob\n");

Euclid’s Game(poj 2348)

題目大意：

給定兩個整數a, b。Alice和Bob輪流用較大的數減去較小的數的整數倍， 並且相減之後的值不小於0。 如果在自己的回合之內， 相減之後的結果為零， 那麼獲勝。Alice先手。

根據上述兩個問題我們有兩個規律可以用上：1.將大問題劃分為小問題在進行解決 2.尋找開始（或結束）位置的必敗態（或必勝態）在加以正推（或倒推）；

劃分： 我們按照後續處理的差別， 將其分為3類：
1.b < a, 我們將a b 進行交換， 使得b恆大於a；
2.a > (b - a)；
3.a < (b - a) ;

對於第一種情況， 為了便於後續處理， 我們將其認為是預設情況；
對於第二種情況， 我麼可以選擇在b 的基礎上減去 a， 或者減去2a和以上；（這一種是有餘地的方案）
對於第三種情況， 我們僅僅只有減去a這一種方法；

對於第一種情況：預設的調整方式， 我們用來調整a，b代表的值， 在這裡不用討論（這裡實際指的就是swap函式的呼叫過程）
對於第三種情況， 僅僅只有一種方案： 繼續向下迭代， 直到出現最終結局；
對於第二種情況： 假設x是使b - ax < a成立的整數， 那麼在第二種情況中又可以分為兩種情況 I. b - ax; II.b - a(x - 1);

下面我們討論 二.I： 這種情況和第三種情況類似， 只能向下迭代， 尋找最終的結果；
對於情況二.II：這種情況的後繼情況就是情況就只有b - ax這一種情況， 很巧， 這又回到了情況三。而經過了兩次轉換， 這種情況依舊是必勝態；

int a, b;

bool flag = true;
while(true)
{
    if(a > b)
        swap(&a, &b);

    if(b % a == 0)
        break;

    if(b - a > a)
        break;

    b -= a;
    flag = !flag; 
}
if(flag)
    printf("Alice!\n");
else
    printf("Bob!\n");