2D射影幾何和變換
阿新 • • 發佈:2018-12-31
閱讀《計算機視覺中的多檢視集合》
2D射影幾何和變換
2D射影平面
本章的關鍵是理解線和點的對偶性。從射影平面模型出發,IP^2^內的點(a, b ,c)由IP^3^空間中一條過原點的射線k(x1, x2, x3)^T^表示。點採用的是齊次座標表示,具有相同比例,不同縮放因子的表示都是同一個點,就像射線也可以用同比例,不同縮放因子的向量表示一樣。
射影變換projectivity
- 射影對映,也叫保線變換,或者射影變換,或者單應(homography),都是同義詞,其性質是保線性,即直線變換之後還是直線。 可以用一個8自由度的三維非奇異矩陣H表示。
- 只需要4個任意三點不共線的點即可以求得射影變換H,然後求得逆矩陣H^-1^即可以消除射影變換H帶來的變化。
- 透視變換,也即中心投影,是射影變換的一種,它的特點是:連線對應的直線共點。透視變換的複合不再是透視變換,但還會是射影變換。
如果有一個射影變換H,點x變換之後為Hx,那麼在同樣的變換下,直線I變換為H^-T^I。我們稱點的變換為逆變,線的變換為協變。
變換的層次
如下表,下層的都是上層變化的特例。
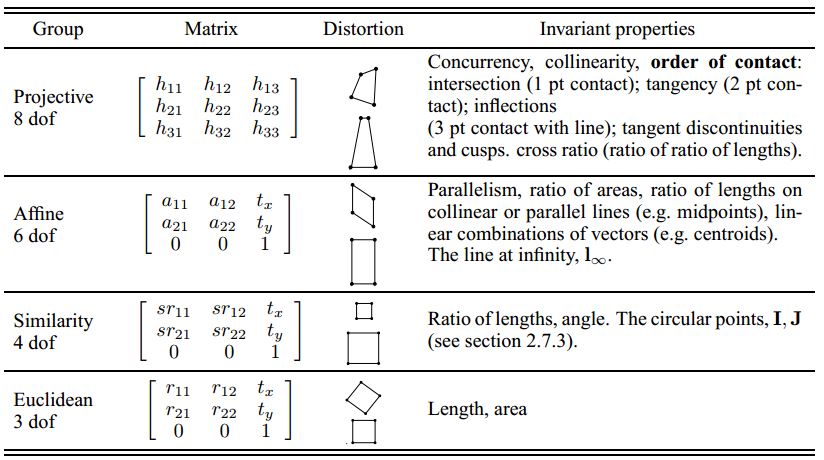
另外還有一個透視變換perspectivity,它是射影變換的一個特例,與仿射變換affine的區別:
- 透視變換可以用於把3D變成2D,而仿射變換都是2D平面
- 透視變換可以有切變shareing
- 仿射變換的右下角必須為1,而透視不會
- 如果是兩個平面的投射,且都是Euclidean座標,那麼透視變換也只有6個自由度
透視變換與射影變換的區別:
- 多個透視變換的組合還會是射影變換,但一般不會是透視變換
- 透視變換中,連線原始點和透視點的所有連線交於一點,這也即是中心投影的含義。
從圖線恢復仿射和度量性質
重要概念
- 理想點:在齊次表示法中,最後座標為0,比如二維座標中的\(x_3=0\),的點即為理想點,也即無窮遠點,通用表達為\((x_1, x_2, 0)^T\)
- 無窮遠線:用符號\(I_{\infty}\)表示,\(I_{\infty}=(0,0,1)^T\),顯然,\((0,0,1)(x_1, x_2, 0)^T=0\),即理想點和無窮遠線相交
- 消影線:無窮遠線被影像到像平面的直線
- 虛圓點:在\(I_{\infty}\)上有兩個不動點\(I=(1,i,0)\)和\(J=(1,-i,0)\),這兩個點是不動點的衝要條件為相似變換,\(I'=H_SI=I\),\(J'=H_SJ=J\),\(H_S\)表示相似變換矩陣, 即經過相似變換,他們的座標不變。
與虛圓點對偶的二次曲線:記為\(C^*_{\infty}\),\(C^*_{\infty}=IJ^T+JI^T=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0\\ 0& 0 & 0 \end{bmatrix}\)。同理,根據對偶定理,二次曲線\(C^*_{\infty}\)為不動曲線的衝要條件為變換為相似變換。
直接從透檢視像恢復
對應的書本中的例 1.26。
- 假設有任意射影變換H
- 根據書中結論1.23,找到五組世界平面中相互正交的直線對,找到他們在變換之後的影象中的對應像直線,即可以求得經過變換H之後的\(C^*_{\infty}\)的像\(C^{*'}_{\infty}\)
根據結論1.24,對\(C^{*'}_{\infty}\)進行SVD分解,即可得到一個變換U,用這個U對像進行校正,就會得到一個與H變換之前只相差一個相似變換的結果。這樣我們就可以根據相似變換的不動量特性來測量某些資料。
分層法恢復
- 在世界平面中平行的兩組平行線,找到他們在像中的對應線,然後找到他們的交點,兩組平行線就會有兩組交點,根據平行線交於無窮遠點的理論,這兩個交點的連線就是消影線。然後根據公式1.18就可以得到一個變換H,可以把像變換到和世界平面只差一個仿射變換
在已經只存在仿射變換的影象中,找到兩對在世界平面中正交的直線的像,然後根據結論1.23就可以求出仿射變換矩陣K。這個K把一個與世界平面只差一個相似變換的平面變換到當前仿射變換影象。
