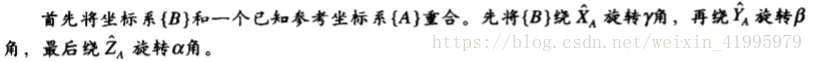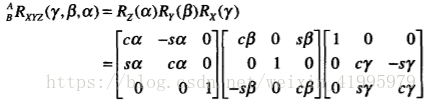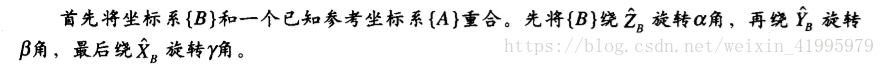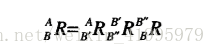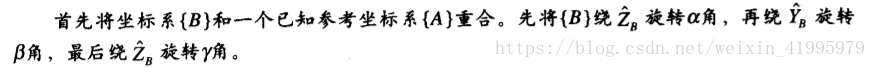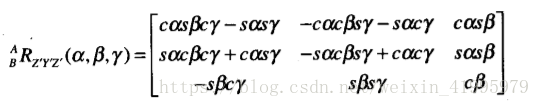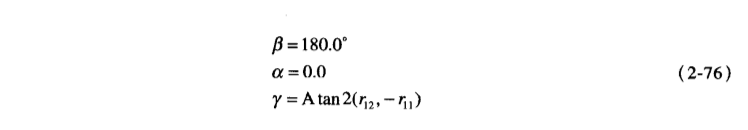0.姿態的其他描述方法

如果你也有看機器人學導論的原書的話，可能會看到這樣一個東西：正交矩陣的凱萊公式。不知道你是怎麼樣的，反正我是一臉懵逼，有這麼個東西嗎？百度好像也找不到呀，最後還是靠谷歌和原書的參考文獻才找到這麼個東西的。
正交矩陣的凱萊公式

0.0 X-Y-Z固定角座標系

下面介紹一種描述座標系{B}姿態的方法：

我們發現每個旋轉都是圍繞著座標系{A}的軸在進行的，我們稱這種姿態的變換方式叫做X-Y-Z固定角座標系
既然整個旋轉變換都是在一個固定的座標系下進行的，那麼我們就可以直接來推導該旋轉的等價旋轉矩陣：

tip：表示式中出現的‘c’和‘s’其實是“cos”和“sin”的縮寫

將上式進一步化簡得到：

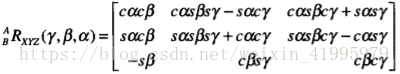
有了這些還不夠，我們可能對如何求出一個旋轉矩陣等價的X-Y-Z固定角座標系。

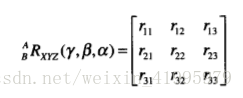
這時候我們可以列出九個方程，但其實我們只有3個未知量，那麼解方程就變得輕鬆起來了

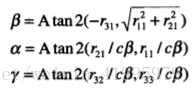
其中的Atan2(x,y)是一個雙引數的反正切函式

很明顯，β的值是±90，那麼在這種情況下，我們只能求出α和γ的和或者差，所以我們一般取α = 0

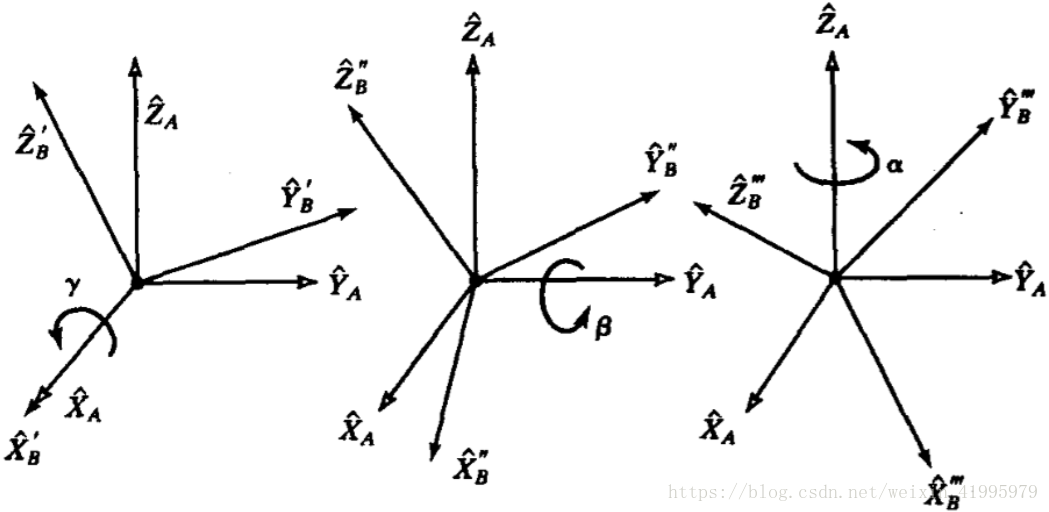
0.1 Z-Y-X尤拉角

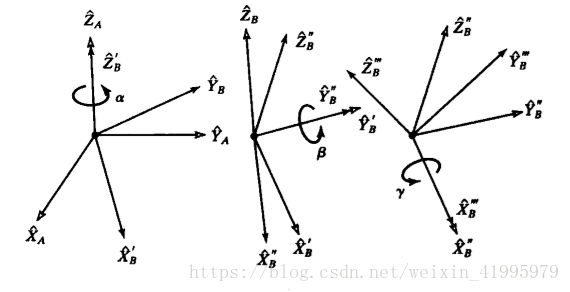
第二種{B}表示方法：


與上一個表示法不同的是：
（1）順序不同：上一個是XYZ，這個是ZYX
（2）旋轉軸不同：上一個是繞固定的旋轉軸，這次是繞運動的旋轉軸
如果把這些旋轉的過程看成座標系的描述，那麼我們可以寫成下面這種形式:

對上式進行展開：

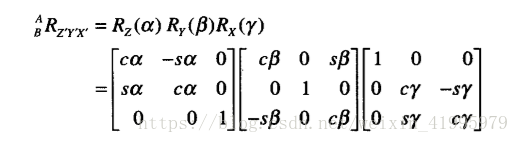
最終我們得到：

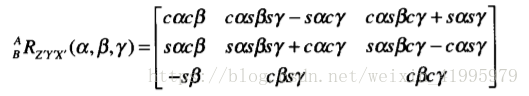
你是否發現，這個結果好眼熟啊，沒錯這跟上一個的結果是一樣的。
這是一個比較隱晦的、不直觀的結果：三次繞固定軸旋轉和按照相反順序繞運動軸旋轉得到的最終姿態是相同的。

0.2 Z-Y-Z尤拉角

類似之前的操作，我們可以得到下式：

那我們照常要來討論一下如何從旋轉矩陣得到Z-Y-Z尤拉角：

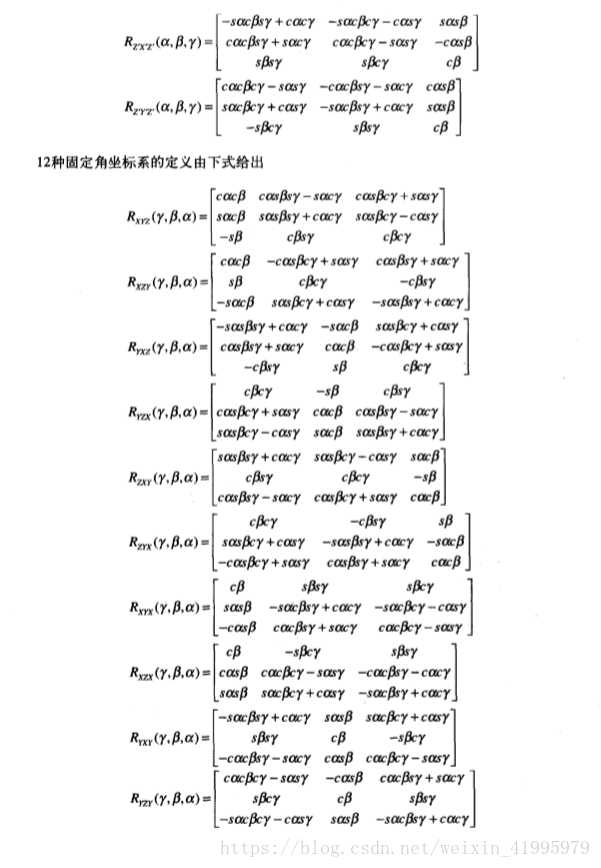
0.3 其他角座標系表示法

以上講了三種表示姿態的常見表示法，每個表示法都需要按照一定的順序進行三次繞主軸的旋轉，這些表示法是24種表示法中的典型方法，且都被稱為角座標系表示法。】

0.4 等效軸角座標表示法

如果給你一個符號Rx(30.0)，你應該知道這是要繞X

軸旋轉30度，這就是一個等效軸角座標表示法的例子。但是如果我們不是要繞某一主軸旋轉，而是在空間中找一個一般的向量作為旋轉軸來旋轉那該怎麼辦呢？
這就可以衍生出一個新的表示法了：


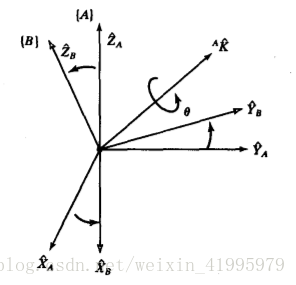
當旋轉軸是一般向量時，其等效旋轉矩陣為：

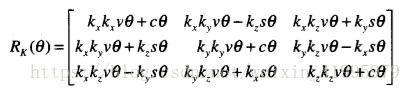
0.5 尤拉引數

另一種姿態表示法是通過四個數值來表示的，稱為尤拉引數