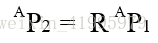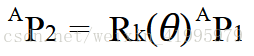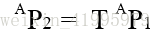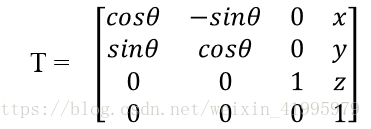機器人學筆記之——空間描述和變換:運算元
阿新 • • 發佈:2018-11-21
0. 運算元:平移、旋轉和變換
用於座標系間點的對映的通用數學表示式稱為運算元,包括點的平移運算元、旋轉運算元和平移加旋轉運算元。
0.0 平移運算元
平移將空間中的一個點沿著一個已知的向量方向移動一定距離。對空間中一點實際平移的描述僅與一個座標系有關。空間中點的平移與此點向另一個座標系的對映具有相同的數學描述,因此弄清楚對映的數學意義是非常重要的。這個區別很簡單:當一個向量相對於一個座標系“向前移動”時,既可以認為是向量“向前移動”,也可以認為座標系“向後移動”,兩者的數學表示式是相同的,只不過是觀察的位置不同。
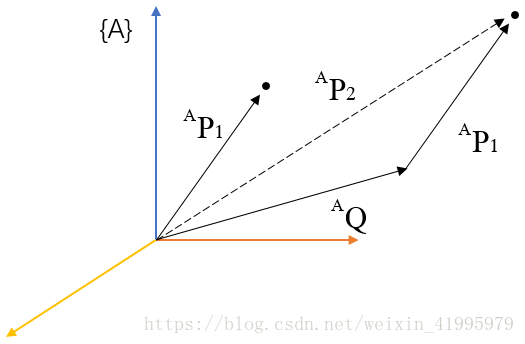
如上圖所示,將aP1沿著aQ
平移的結果是得到一個新的向量
aP2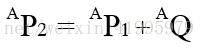
用矩陣運算元寫出的平移變換是:
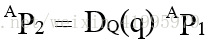
其中:
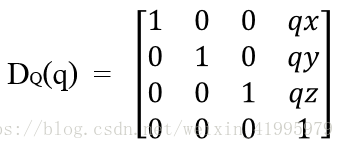
表示式中的
q是沿已知向量方向平移的數量,它也是有符號的。qx、qy、qz是平移和向量Q的分量,而且: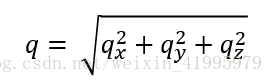
0.1 旋轉運算元
旋轉矩陣還可以用旋轉變換運算元來定義,它將一個向量
aP1用旋轉變成另一個向量aP2
用旋轉運算元寫出的數學表示式是:
旋轉和平移的情況一樣,旋轉變換和旋轉對映的數學表示式相同,只是意義不同。
向量經某一旋轉R得到的旋轉矩陣與一個座標系相對於參考座標系經某一旋轉R得到的旋轉矩陣是相同的。
我們使用另一個符號來表示旋轉運算元以明確說明是繞哪個軸旋轉的:
上式中的
k表示繞K軸旋轉,θ表示旋轉的角度。將這個運算元變成矩陣的形式如下: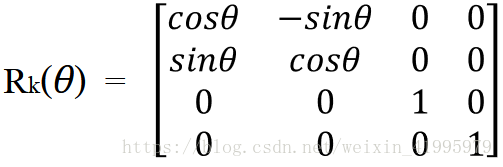
0.2 變換運算元
相同,座標系也可以使用變換運算元來定義。座標系和座標系對映的數學描述也是相同的,也是意義不同。
一個變換通常被認為是由一個廣義旋轉矩陣和位置向量分量組成的齊次變換的形式。
形如下圖:
這就是一個運算元T,表示了繞Z軸旋轉θ度,沿X軸平移x個單位,沿Y軸平移y個單位,沿Z軸平移z個單位