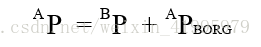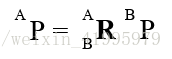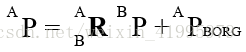0. 對映

在機器人學的許多問題中，都需要使用不同的參考座標系來表達同一個量，為了描述從一個座標到另一個座標的變換，機器人學引入了對映的概念。

0.0 平移座標系的對映

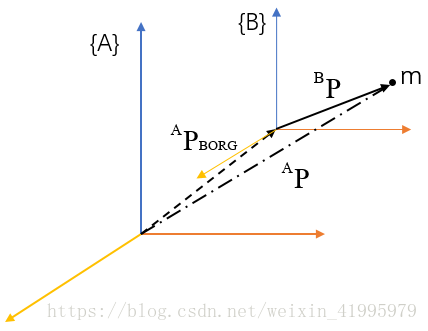
如下圖所示，座標系{A}和{B}的姿態是相同的，在空間中有一個點m，我們希望使用座標系{A}來表示點m，由於兩個座標系是平移關係，所以向量aPborg可以直接表示為{B}相對{A}的位置關係。

在兩個座標系擁有相同姿態這種特殊情況下，我們可以簡單地使用向量的相加求得點m相對座標系{A}的表示——向量aP

將一個向量從一個座標系對映到另一個座標系這整個過程中，矢量表示的點的位置並沒有發生任何改變，只是描述的方式不同了而已。
所以對映的概念就是，“描述”

0.1 旋轉座標的對映

在上一篇博文中，我們看到了用一組三個向量的矩陣來表示座標系的旋轉變換，該矩陣稱為旋轉矩陣。

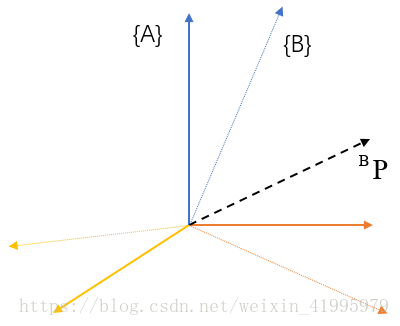
假設現在我們知道一個向量相對於某個座標系的表示，想要得到該向量相對於另一個座標系的表達，而且前後兩個座標系的原點相互重合。也就是說後者是由前者做單純的旋轉變換得到的。
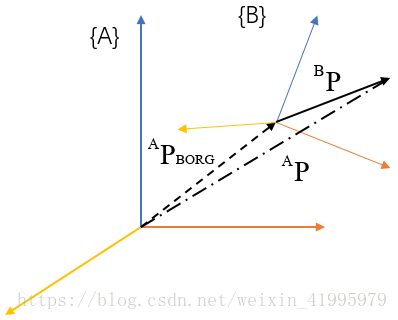
如上圖所示，我們已知bP以及{A}和{B}的變換關係，現在想求出aP
那麼只要用bP與旋轉矩陣相乘就能夠得到aP

0.2 一般座標系的對映

前面說的兩種情況比較特殊，分別只有位置和姿態的變換，那如果上升到座標系層面的變換，即位置和姿態同時變換的時候，對映會是怎麼樣的呢？
現在我們就來考慮對映的一般情況：

整個變換過程一次進行的話比較麻煩，那我們就把他拆開來看，尋找一箇中間座標系，該座標系與{A}的姿態相同，原點與{B}重合。這樣我們就能把變換拆分成先平移後旋轉的方式，無論從直觀上還是從數學上看都會方便很多。

在數學推導的過程中，我們也會使用一種更加簡潔的方式來表達上式