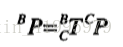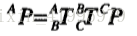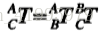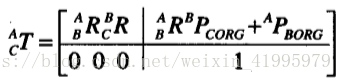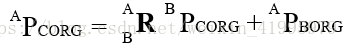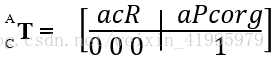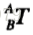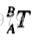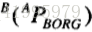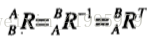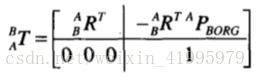機器人學筆記之——空間描述和變換:變換演算法
0. 變換演算法
0.0 混合變換
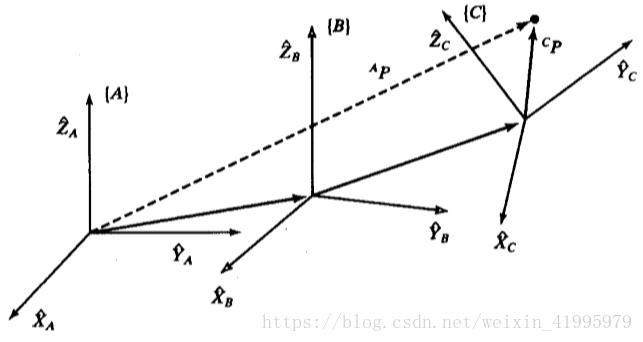
在上圖的中,假設每個座標系相對於前一個座標系都是已知的,現在已知cP要求aP
既然每個座標系相對前一個座標系都是已知的,那麼就意味著我們可以根據cP倒著一步步變換成aP
首先是變換成bP:
然後再由bP變換成aP:
當然,分開寫比較不簡潔,我們依然是比較習慣寫成一個單獨的表示式,那麼只要綜合上述兩個過程,聯立兩條式子,就可以得到下面這條簡單的表示式:
其中:
我們可以求得:
其實我個人更加喜歡從幾何的角度來觀察這個問題,感覺會更加簡單一點。已知cP要求aP的話,我們就需要找到{C}關於{A}的變換運算元,從直觀上看圖就可以知道,這是一個一般的變換運算元,其中包含了旋轉和平移。
首先單純看平移部分,我們可以發現其實是沿著aPcorg平移的,我們又可以得到:
接著我們單純看旋轉部分,我們無法直接得到從{A}到{C}的旋轉矩陣,但是我們知道從{A}到{B}的旋轉矩陣和從{B}到{C}的旋轉矩陣,因此我們可以得到:
至此,我們已經可以根據求得的資訊寫出一個一般變換的運算元了:
其實兩個結果是相同的。
0.1 逆變換
已知座標系{B}相對於{A},為了得到{A}相對於{B}的描述,我們需要求出
的逆,我們可以直接將4x4的齊次變換矩陣求逆得到,但是這樣的操作並沒有使用到變換的性質,我們還可以使用另外一種方式,利用變換的性質求出逆矩陣。
首先我們明確一下要求的目標:
在這裡先忘記前面說的話,我們就單純地把任務看成要求一個變換運算元,那麼我們就得知道旋轉矩陣和位置向量。
那麼任務就變成了,由已知量:
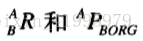
求出未知量:
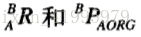
我們從位置向量開始考慮起,我們已知了aPborg,要求bPaorg,那麼就是一個將aPborg從{A}對映到{B}的過程。還記得一般座標系對映是怎麼做的嗎?
bingo~
看著上面這個式子,有沒有什麼想法?
將{B}座標系原點相對於{A}的描述重新映射回{B},那不就是0嗎?
由此可化簡得到:
這就求出bPaorg了。
那麼接下來,我們看一下旋轉矩陣。
我們知道,旋轉矩陣是一個正交矩陣,正交矩陣又有著特殊的性質,其轉置等於逆
所以,輕而易舉,旋轉矩陣也求出來了。
至此,我們就可以得到完整的變換運算元:
這是求齊次變換逆矩陣一般而且有效的方法。