影象離散餘弦變換和反變換
使用的函式:B = dct(A);
功能:實現影象的二維離散餘弦變換。
A為原影象,B為變換後的影象。
使用的函式:B=idct2(A);
功能:實現影象的二維離散餘弦反變換
A為原影象,B為變換後的影象。
原始碼:clc;
clear all;
I=imread('rice.png');
A=dct2(I);
A(abs(A)<1)= 0;
B=idct2(A);
subplot(221)
imshow(I);
subplot(222)
imshow(A);
subplot(223)
imshow(B,[0 255])
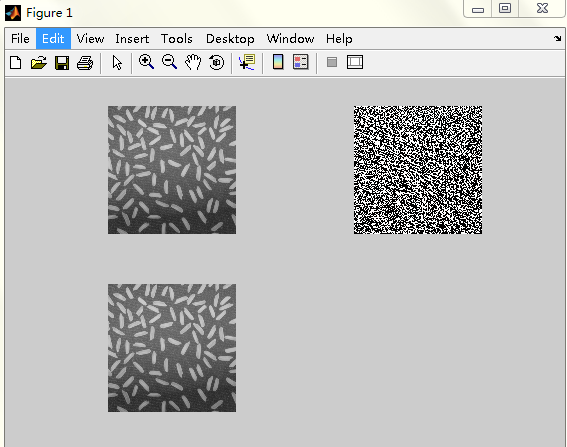
實驗結果:
相關推薦
影象離散餘弦變換和反變換
使用的函式:B = dct(A); 功能:實現影象的二維離散餘弦變換。 A為原影象,B為變換後的影象。 使用的函式:B=idct2(A); 功能:實現影象的二維離散餘弦反變換 A為原影象,B為變換後的影象。 原始碼:clc; clear all; I=imread(
影象處理二:仿射變換和透視變換
一、仿射變換(Affine Transformation) 放射變換(平面變換、二維座標變換):是空間直角座標系的變換,從一個二維座標變換到另一個二維座標,仿射變換是一個線性變換,保持了影象的“平行性”和“平直性”,即影象中原來的直線和
opencv3 離線餘弦變換和逆變換
程式碼如下 #include<opencv.hpp> int main() { cv::Mat image; cv::Mat dctimage; image = cv::imread("F:\\ebook\\opencv\\LearningOpenCV3\\tes
OpenCV下利用傅立葉變換和逆變換實現影象卷積演算法,並附自己對於卷積核/模板核算子的理解!
學過訊號與系統的人都知道,卷積運算一般是轉化成頻率乘積再求逆來計算,因為這樣可以減少計算量,提高程式碼的效率。 影象卷積操作廣泛應用在影象濾波技術中。 影象卷積運算中一個重要概念是卷積核算子,它是模板核算子的一種,模板核算子實際上就是一個視窗矩陣,用這個視窗按畫素點滑動去
Opencv中的仿射變換和透射變換
OpenCV提供了一些關於透視變換的介面,例如getPerpectiveTransform, warpPerspective等。這裡主要說明一下warpPerspective是如何工作的。 其實OpenCV中很多影象變換的對映關係都是反直覺的,如這裡的warpPerspe
OpenCV練習:仿射變換和透射變換
#coding=utf-8</code> import cv2 import numpy as np from matplotlib import pyplot as plt img=cv2.imread('1.jpg') rows,cols,ch=img.shape pts1=np.
仿射變換和投影變換
1. 仿射變換 1) 用途 旋轉 (線性變換),平移 (向量加).縮放(線性變換),錯切,反轉 2) 方法 仿射變換是一種二維座標到二維座標之間的線性變換,它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二維圖形之間的相對位置關係保持不變,平行線依然是平行線,
傅立葉變換和拉普拉斯變換
尤拉公式 證明過程如下 首先是泰勒展開 參考cosX和sinX的泰勒展開可以證明這個問題。 還有下面這個號稱宇宙最美公式 “自然底數e,自然數1和0,虛數i還有圓周率pi,它是這麼簡潔,這麼美麗啊!” 傅立葉級數 傅立葉在提出傅立葉變換時,堅持認為任何一個週期訊號都可
傅立葉變換和逆變換公式的我理解意義
f(t)的傅立葉變換F(w)=∫ f(t) *e(-iwt)dt ,由於(1,sinwx,coswx,sin2wx,cos2wx,... sinnwx,cosnwx,....)是一組正交函式,傅立葉變換從公式來看就是內積,只有f(t)中含有對應w分 量才能有內積不為零,有
仿射變換和透射變換
仿射變換 定義:仿射變換的功能是從二維座標到二維座標之間的線性變換,且保持二維圖形的“平直性”和“平行性”。仿射變換可以通過一系列的原子變換的複合來實現,包括平移,縮放,翻轉,旋轉和剪下。 這類變換可以用一個3*3的矩陣M來表示,其最後一行為(0,0,1)。該變換矩陣
Python 實現影象快速傅立葉變換和離散餘弦變換
影象的正交變換在數字影象的處理與分析中起著很重要的作用,被廣泛應用於影象增強、去噪、壓縮編碼等眾多領域。本文手工實現了**二維離散傅立葉變換**和**二維離散餘弦變換**演算法,並在多個影象樣本上進行測試,以探究二者的變換效果。 ## 1. 傅立葉變換 ### 實驗原理 對一幅影象進行**離散傅立葉變換
DCT(離散餘弦變換)演算法原理和原始碼(python)
原理: 離散餘弦變換(DCT for Discrete Cosine Transform)是與傅立葉變換相關的一種變換,它類似於離散傅立葉變換(DFT for Discrete Fourier Transform),但是隻使用實數。離散餘弦變換相當於一個長度大概是它兩倍的離散傅立葉變換,這個離散傅立
案例解釋影象傅立葉變換的幅度譜和相位譜的以及反變換
目的:讀取影象 A(lena.tiff)和B(rice.tif),顯示這兩幅影象,對影象作傅立葉變換,顯示影象的傅立葉幅度譜和相位譜。做傅立葉逆變換,顯示重建影象。 影象的頻率是表徵影象中灰度變
DFT(離散傅立葉變換)和DCT(離散餘弦變換)有何區別和聯絡
首先,在理解這3個變數之前,你要知道DTFT: DTFT是離散時間傅立葉變換,用來表達連續的訊號的頻譜。 然後理解DFT: DFT是離散傅立葉變換,針對的是離散的訊號和頻譜。DFT是DTFT變化而來,其
第四天 opencv 影象變換和空間影象濾波
####################這段是轉載,解釋影象變換和空間濾波區別即cv.medianBlur和cv.filter2D####### 在空間域的操作主要可以分為兩類:第一類是所謂的“影象強度變換”(Intensity Transform),另一類是所謂的“空間域影象濾波”(Spati
DCT 離散餘弦變換 DiscreteCosineTransform
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
影象演算法-灰度變換 反色 對數變換 伽馬變換
常用的灰度變換 在影象處理中,灰度影象為單通道,灰度值範圍為[0, 255];彩色影象的為RGB三通道,每個通道的畫素值的範圍也是[0, 255]。灰度變換就是一組對映關係,通過這組對映關係的運算,實現影象效果的變化。下面主要介紹影象反色、對數變換、伽馬變換三
【 MATLAB 】逆離散餘弦變換(idct)的基礎知識介紹
基礎知識介紹 逆離散餘弦變換從離散餘弦變換 (DCT) 係數中重建序列。idct 函式是 dct 函式的逆。 The DCT has four standard variants. For a tr
Opencv影象處理---基於距離變換和分水嶺演算法的影象分割
程式碼 #include <opencv2/opencv.hpp> #include <iostream> using namespace std; using namespace cv; int main(int, char** argv) {
第四天 opencv 影象變換和空間影象濾波
####################這段是轉載,解釋影象變換和空間濾波區別即cv.medianBlur和cv.filter2D####### 在空間域的操作主要可以分為兩類:第一類是所謂的“影象強度變換”(Intensity Transform),另一類是所謂的“空間域