很妙的一道題

感覺又加深了對\(KMP\)還有\(next\)陣列的理解

先來看看這個鬼畜的題意，大致就是給你一個字串，對於這個字串的每一個字首，要去找到這個字首的一個最長的字首，使得字首成為這個字首的字首倍長之後的字首

很蛇皮的題意，之後可能就會懵逼了，這根\(KMP\)有什麼關係

我們來考慮這樣一張圖

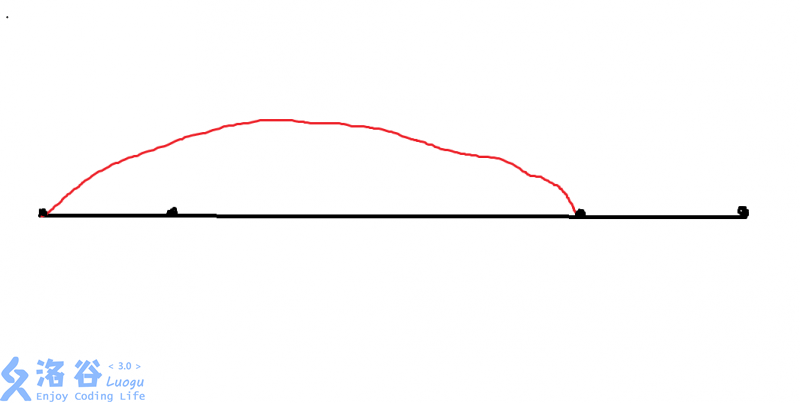
那個標這黑點的部分是這個字首\(i\)的\(next[i]\)，於是我們如果將這個紅色的部分倍長，這個相等的字首和字尾就可以卡到一起了，於是就滿足了字首成為這個字首的字首倍長之後的字首的要求

但是這顯然不能夠滿足最長的字首這個要求

很顯然這個紅色的字首長度為\(i-next[i]\)

怎麼讓\(next[i]\)變小呢，很顯然我們多跳幾次\(next\)就好了，直到我們跳\(next\)跳不動了，那麼我們就找到了最短的相等字首和字尾，這個時候紅色部分就是最長的了

所以我們可以寫一個暴力跳\(next\)的程式碼

#include<iostream>
#include<cstdio>
#include<cstring>
#define re register
#define maxn 1000005
#define LL long long
char S[maxn];
int nx[maxn];
int n;
LL ans;
int main()
{
    scanf("%d",&n);
    scanf("%s",S+1);
    nx[0]=nx[1]=0;
    for(re int i=2;i<=n;i++)
    {
        int p=nx[i-1];
        while(p&&S[p+1]!=S[i]) p=nx[p];
        if(S[i]==S[p+1]) nx[i]=p+1;
        else nx[i]=0;
    }
    for(re int i=1;i<=n;i++)
    {
        int p=nx[i];
        if(!p) continue;
        while(nx[p]) p=nx[p];
        ans+=i-p;
    }
    printf("%lld",ans);
    return 0;
}
 

顯然暴力跳\(next\)很容易被卡成\(O(N^2)\)，我們得有一個更妙的方法來得到一個字首的最短非空相等字首字尾

於是我們設\(num[i]\)表示\(i\)這個字首的最短相等字首字尾的長度

於是答案就是\(\sum_{i=1}^ni-num[i]\)

對於這個\(num\)陣列我們還是可以在求\(next\)的時候順便求出來

如果一個\(i\)和某個位置\(p+1\)匹配上了，那麼\(num[i]=num[p+1]\)顯然\(i\)最後跳下去也就是\(num[p+1]\)得到的最短相等字首字尾

如果沒有匹配上\(num[i]=i\)，\(num\)等於自己

程式碼

#include<iostream>
#include<cstdio>
#include<cstring>
#define re register
#define maxn 1000005
#define LL long long
char S[maxn];
int nx[maxn],num[maxn];
int n;
LL ans;
int main()
{
    scanf("%d",&n);
    scanf("%s",S+1);
    nx[0]=nx[1]=0;
    num[1]=1;
    for(re int i=2;i<=n;i++)
    {
        int p=nx[i-1];
        while(p&&S[p+1]!=S[i]) p=nx[p];
        if(S[i]==S[p+1]) nx[i]=p+1,num[i]=num[p+1];
        else nx[i]=0,num[i]=i;
    }
    for(re int i=2;i<=n;i++)
        ans+=(i-num[i]);
    printf("%lld",ans);
    return 0;
}