概率空間與概率分佈
阿新 • • 發佈：2019-01-02
若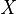
服從引數為
的泊松分佈，記為
，或記為
.
性質
1、服從泊松分佈的隨機變數，其數學期望與方差相等，同為引數λ：E(X)=V(X)=λ
2、兩個獨立且服從泊松分佈的隨機變數，其和仍然服從泊松分佈。更精確地說，若X ~ Poisson(λ1)且Y ~ Poisson(λ2)，則X+Y ~Poisson(λ1+λ2)。
3、其矩母函式為：
![M_X(t)=E[e^{tX}]=\sum_{x=0}^\infty e^{tX}\frac{e^{-\lambda}\lambda^x}{x!}=e^{-\lambda}\sum_{x=0}^\infty\frac{({e^t}\lambda)^x}{x!}=e^{{\lambda}(e^t-1)}](https://upload.wikimedia.org/math/a/4/0/a40546829ef4788b3ef7aa7e28cd1f13.png)
泊松分佈的來源（泊松小數定律）
在二項分佈的伯努利試驗中，如果試驗次數n很大，二項分佈的概率p很小，且乘積λ= np比較適中，則事件出現的次數的概率可以用泊松分佈來逼近。事實上，二項分佈可以看作泊松分佈在離散時間上的對應物。
證明如下。首先，回顧e的定義：
二項分佈的定義：
-
。
如果令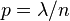
, 
趨於無窮時
的極限：
![\begin{align}\lim_{n\to\infty} P(X=k)&=\lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k} \\ &=\lim_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}\\&=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \lim_{n\to\infty}\underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\end{align}](https://upload.wikimedia.org/math/0/9/8/098dfaad42d2f1765750172fe9d0ad71.png)
最大似然估計
給定n個樣本值ki，希望得到從中推測出總體的泊松分佈引數λ的估計。為計算最大似然估計值，列出對數似然函式：
對函式L取相對於λ的導數並令其等於零：
解得λ從而得到一個駐點（stationary point）：
檢查函式L的二階導數，發現對所有的λ與ki大於零的情況二階導數都為負。因此求得的駐點是對數似然函式L的極大值點：
例子
對某公共汽車站的客流做調查，統計了某天上午10:30到11:47來到候車的乘客情況。假定來到候車的乘客各批（每批可以是1人也可以是多人）是互相獨立發生的。觀察每20秒區間來到候車的乘客批次，共觀察77分鐘*3=231次，共得到230個觀察記錄。其中來到0批、1批、2批、3批、4批及4批以上的觀察記錄分別是100次、81次、34次、9次、6次。使用極大似真估計（MLE），得到
生成泊松分佈的隨機變數一個用來生成隨機泊松分佈的數字（偽隨機數抽樣）的簡單演算法，已經由高德納給出（見下文參考）：
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p×u.
while p > L.
return k − 1.
儘管簡單，但複雜度是線性的，在返回的值k
對於很小的λ值，逆變換取樣簡單而且高效，每個樣本只需要一個均勻隨機數u。直到有超過u的樣本，才需要檢查累積概率。
algorithm Poisson generator based upon the inversion by sequential search:[1]init:
Let x ← 0, p ← e−λ, s ← p.
Generate uniform random number u in [0,1].
do:
x ← x + 1.
p ← p * λ / x.
s ← s + p.
while u > s.
return x.