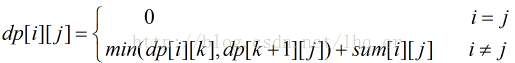石子合併(NOI1995)
阿新 • • 發佈:2019-01-29
F: 石子合併(NOI1995)
時間限制: 1 Sec 記憶體限制: 128 MB
題目描述
在操場上沿一直線排列著 n堆石子。現要將石子有次序地合併成一堆。規定每次只能選相鄰的兩堆石子合併成新的一堆, 並將新的一堆石子數記為該次合併的得分。允許在第一次合併前對調一次相鄰兩堆石子的次序。
計算在上述條件下將n堆石子合併成一堆的最小得分和初次交換的位置。
輸入
輸入資料共有二行,其中,第1行是石子堆數n≤100;
第2行是順序排列的各堆石子數(≤20),每兩個數之間用空格分隔。
輸出
輸出合併的最小得分。
樣例輸入
3
2 5 1
樣例輸出
11
Solution
石子合併問題是最經典的 DP問題。首先它有如下3種題型:
1.有N堆石子,現要將石子有序的合併成一堆,規定如下:每次只能移動任意的2堆石子合併,合併花費為新合成的一堆石子的數量。求將這N堆石子合併成一堆的總花費最小(或最大)。
分析:當然這種情況是最簡單的情況,合併的是任意兩堆,直接貪心即可,每次選擇最小的兩堆合併。本問題實際上就是哈夫曼的變形。
2.有N堆石子,現要將石子有序的合併成一堆,規定如下:每次只能移動相鄰的2堆石子合併,合併花費為新合成的一堆石子的數量。求將這N堆石子合併成一堆的總花費最小(或最大)。
分析:我們熟悉矩陣連乘,知道矩陣連乘也是每次合併相鄰的兩個矩陣,那麼石子合併可以用矩陣連乘的方式來解決。
設dp[i][j]表示第i到第j堆石子合併的最優值,sum[i][j]表示第i到第j堆石子的總數量。那麼就有狀態轉移公式:
當然這裡可以用到強大的平行四邊形優化,證明過程看檔案
注意:此題可以交換相鄰的石子堆,暴力列舉即可。
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int maxn=110; int dp[maxn][maxn],s[maxn][maxn]; int sum[maxn],a[maxn]; int n,ans=0x3f3f3f3f; void work() { sum[0]=0; memset(dp,0x3f,sizeof(dp)); for (int i=1;i<=n;i++) { sum[i]=sum[i-1]+a[i]; dp[i][i]=0; } for (int i=1;i<=n-2+1;i++) { int j=i+2-1; dp[i][j]=dp[i][i]+dp[i+1][j]+sum[j]-sum[i-1]; s[i][j]=i; } for (int len=3;len<=n;len++) for (int i=1;i<=n-len+1;i++) { int j=i+len-1; for (int k=s[i][j-1];k<=s[i+1][j];k++) if (dp[i][j]>=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) { dp[i][j]=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]; s[i][j]=k; } } if (ans>dp[1][n]) ans=dp[1][n]; } int main() { cin>>n; for (int i=1;i<=n;i++) cin>>a[i]; work(); for (int l=1;l<=n-1;l++) { swap(a[l],a[l+1]); work(); swap(a[l],a[l+1]); } cout<<ans<<endl; }