Loss Function總結
開始比較糾結於Cost/Error Function和Loss Function之間的區別，後來發現它們在數學優化問題上其實是一回事，見這裡。因此以下主要以LossFunction進行總結。
一、什麼是Loss Function
wiki上有一句解釋很到位，引用一下：The loss function quantifies the amount by which the prediction deviates from the actual values。Loss Function中文損失函式，適用於用於統計，經濟，機器學習等領域，雖外表形式不一，但其本質作用應是唯一的，即用於衡量最優的策略。本章只從機器學習（ML）領域來對其進行闡述，機器學習其實是個不停的模擬現實的過程，比如無人駕駛車，語音識別，流感預測，天氣預報，經濟週期行為等眾多領域，是網際網路發展過程中“科學家”（暫且這麼稱呼吧）對於人類文明進步的另一個貢獻，其本質就是要建立一個數學模型用於模擬現實，越接近真實越好，那麼轉化為數學語言即LF越小越好，因為LF值代表著現實與學習預測的差距，這個不停的縮小LF值的過程就稱為優化，如果理解這些的話，就不難理解優化問題對於ML來說的重要性了，如水之於魚，魂之於人！
通常而言，損失函式由損失項(loss term)和正則項(regularization term)組成。可以參考這篇文章：
(1)損失項
•對迴歸問題，常用的有：平方損失(for linear regression)，絕對值損失；
•對分類問題，常用的有：hinge loss(for soft margin SVM)，log loss(for logistic regression)。
說明：
•對hinge loss，又可以細分出hinge loss（或簡稱L1 loss）和squared hinge loss（或簡稱L2 loss）。國立臺灣大學的Chih-Jen Lin老師釋出的Liblinear就實現了這2種hinge loss。L1 loss和L2 loss與下面的regularization是不同的，注意區分開。
(2)、正則項
•常用的有L1-regularization和L2-regularization。上面列的那個資料對此還有詳細的總結。
二、幾種Loss Function概述
如上一節所述，LF的概念來源於機器學習，同時我們也知道機器學習的應用範圍相當廣泛，幾乎可以涵蓋整個社會領域，那麼自然不同的領域多少會有不同的做法，這裡介紹在一般的機器學習演算法中常見的幾種，具有概括性。
2.1一般形式
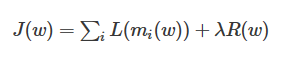
該方程分為兩個部分：L+R，L表示loss term，其中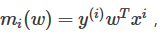 
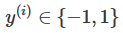
2.2 一般的loss term有5種
•Gold Standard (ideal case)
•Hinge (SVM, soft margin)
•Log (logistic regression, cross entropy error)
•Squared loss (linear regression)
•Exponential loss (Boosting)
分別用於5種常見的機法器學習演算法
Gold Standard（標準式）用於理想sample，這種一般很少有實踐場景，這個方法的作用更多的是用來衡量其他LF的效用；Hinge用於soft-margin svm演算法；log用於LR演算法（Logistric Regression）；squared loss用於線性迴歸 （Liner Regression）和Boosting。
(1)Gold Standard loss，
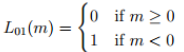
從公式我們可以很清楚的看出，當m<0的時候L=1，m<0說明預測失敗，那麼Loss則加1，這樣將錯誤累加上去，就是Gold Standard loss的核心思想。
(2)hinge loss，常用於“maximum-margin”的演算法，公式如下:
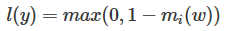
這個公式也很好理解，其中
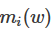表示樣本i在模型下的預測值的樣本i的類標記{-1,1}的乘積，這個乘積可以用來檢驗預測與真實結果是否一致來表示分類是否正確，當乘積大於0時表示分類正確，反之亦然。 (3)log loss(一般又稱為基於最大似然的負log loss):
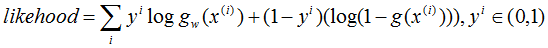
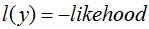
其中
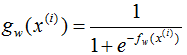是sigmoid函式。 最大似然思想指的是使得某種情況發生的概念最大的思想，根據LR的思想(參考logistic迴歸深入篇（1）)），我們知道g(w)對應的simod圖，其將實域上的值對映到區間{0,1}，因此我們可以把g(w)看作事件A發生的概率，那麼1-g(w)可以看作事件A不發生的概率，那麼公式likelihood表達的含義就很明顯了，y也是一個概率值，可以看做是對事件A與A逆的分量配額，當然我們的期望是A發生的可能越大越好，A逆發生的可能越小越好！因此likelihood是一個max的過程，而loss是一個min的過程，因此log loss是負的likelihood。
(4)square loss
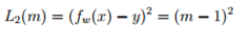
這個loss很好理解，就是平方差。
(5)boosting loss
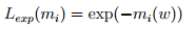
這個loss主要是基於指數函式的loss function。
三、幾種Loss Function的效果對比
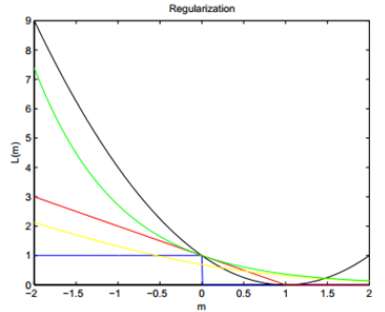
上圖是多LF的效果對比圖，其中藍色的是Gold loss，可以看作水平基線，其他的loss的效果可以基於與它的比較結果，首先，紅色的是Hinge loss，黃色的是log loss，綠色的是boosting loss，黑色的是square loss，從上圖可以看出以下結論： Hinge，log對於噪音函式不敏感，因為當m<0時，他們的反應不大，而黑線與綠線可能更愛憎分明，尤其是黑線，因此，在很多線性分類問題中，square loss也是很常見的LF之一。