圖論（Graph Theory）

1.連通性

2.二分圖

3.網路流

連通性：

pre_: 深度優先遍歷

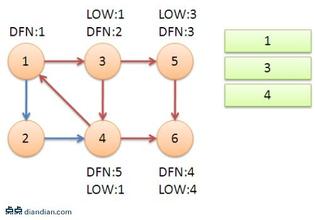
遍歷過程中按照節點經過的時間先後順序給每個節點一個標號——時間戳，記為dfn[x]。時間戳為x的節點的原編號記為id[x]，即id[dfn[x]]=x。

搜尋樹上邊的分類：

樹枝邊 (tree arcs)： 邊(x,y)在搜尋樹T中；

前向邊 (forward arcs)：在T中存在一條從x到y的路徑；

後向邊 (cycle arcs)：在T中存在一條從y到x的路徑；

橫叉邊 (cross arcs)：在T中既沒有x到y的路徑，也沒有y到x的路徑，並且dfn[y] < dfn[x]

注：
以上不是一個圖本身有的概念，應該是圖進行DFS時才有的概念。圖進行DFS會得到一棵DFS樹（森林），在這個樹上才有了這些概念。

強聯通分量：（SCC）

有向圖強連通分量：在有向圖G中，如果兩個頂點vi,vj間（vi>vj）有一條從vi到vj的有向路徑，同時還有一條從vj到vi的有向路徑，則稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通，稱G是一個強連通圖。有向圖的極大強連通子圖，稱為強連通分量(strongly connected components)。 —— [ 百度百科 ]

Tarjan：

這個人，
證明了並查集的複雜度，發明了Splay，發明了動態樹。
更重要的是，他發明了Tarjan演算法。

用到的變數：

dfn[u]：節點u的時間戳，表示點u是第幾個被訪問的點
low[u]：是u或u的子樹能追溯到的最早的棧中節點的dfn

當dfn[u]=low[u]時，以u為根的搜尋子樹上所有節點（從棧頂到u的所有節點）為一個強聯通分量

演算法：

1. 如果x->y是樹枝邊，那麼 low[x]=min{low[x],low[y]}
2. 如果x->y是後向邊，那麼 low[x]=min(low[x],dfn[y])
3. 如果x->y是橫叉邊，什麼也不做

Code：

void tarjan(int rt)
{
    int j;
    dfn[rt]=low[rt]=++dep;
    stack[++top]=rt;
    for
 
(int j=head[rt];j!=-1;j=edge[j].next)
    {
        int to=edge[j].to;
        if(dfn[to]==0)
        {
            tarjan(to);
            low[rt]=min(low[rt],low[to]);
        }
        else if(same[to]==0)
        {
            low[rt]=min(low[rt],dfn[to]);
        }
    }
    if(low[rt]==dfn[rt])
    {
        scc_cnt++;
        int t=0,v;
        do
        {
            t++;
            v=stack[top--];
            same[v]=scc_cnt;
        }
        while(v!=rt);
        scc_num[scc_cnt]=t;
    }
}

例題：POJ 1236 / POJ 2762 / BZOJ 2330

2-SAT問題：

模型：

給定n對數，每一對中必須且僅能取一個數，某些數i,j之間有矛盾，不能同時被取，求可行性，以及一種方案.

Solution:

1.構圖（若取i後必須取j則i,j之間有邊）
2.Tarjan 求強聯通分量
3.若n對中有某一對在同一個強聯通分量中，則無解
4.輸出解：自底向上 拓撲排序 ，每次找到能夠取出的零出點i，標記與i同一對的點不能取

時間複雜度為O(N+M)

例題：BZOJ1997

Add：李煜東的成績論

1.見過很多的模型，往已知上靠
2.智商問題，想不出來
3.想到了寫不出來，程式碼能力問題
。。。。。。

無向圖

割點：

如果在圖G中去掉一個頂點(自然同時去掉與該頂點相關聯的所有邊)後，該圖的連通分支數增加，則稱該頂點為G的割點(cut-vertex)。

·對於一條搜尋樹上的邊（u，v），其中u是v的父節點，若low[v]>=dfn[u],則u為割點

橋

（割邊）圖G的邊e是割邊，當且僅當e不在G的任何一個圈上。
·對於一條搜尋樹上的邊（u，v），其中u是v的父節點，若low[v]>dfn[u],則（u，v）是橋 //注意重邊！
· 樹的所有邊均為橋

雙聯通分量:

點雙連通圖：點連通度大於1的圖（無割點）
邊雙連通圖：邊連通度大於1的圖（無割邊）

演算法：

對於每一條與u相連的邊（u,v）
若搜尋樹上v是u的子節點，更新low[u]=min(low[u],low[v])
若不是，則更新dfn[u]=min(dfn[u],dfn[v])
Code:

int tarjan(int rt,int fa)
{
    dfn[rt]=low[rt]=++dep;
    stack[++top]=rt;
    for(int j=head[rt];j!=-1;j=edge[j].next)
    {
        int to=edge[j].to;
        if(to==fa)continue;
        if(dfn[to]==0)
        {
            tarjan(to,rt);
            low[rt]=min(low[rt],low[to]);
        }
        else if(same[rt]==0)
        {
            low[rt]=min(low[rt],dfn[to]);
        }
        if(low[to]>dfn[rt])
        {
            cut_cnt++;
        }
    }
    if(low[rt]==dfn[rt])
    {
        scc_cnt++;
        int t=0,v;
        do{
            t++;
            v=stack[top--];
            same[v]=scc_cnt;
        }while(v != rt);
        scc_num[scc_cnt]=t;
    }
}

例題：POJ2942(建補圖) / Violet 6

Add:LCA求法總結

LCA (最近公共祖先)

暴力做法 O(N^2)
Tarjan演算法離線處理 O(N+M+Q) <接近線性，最快的方法>

必經點與必經邊：

無向圖：

• Tarjan求出雙聯通分量，所點後建樹；
• 對於每個詢問通過LCA計算：

有向無環圖:

• 求S道每個點的路徑條數CntS,每個點到T的路徑條數CntT；
• 若邊（u，v）滿足Cnt

Tarjan的擴充套件：一般有向圖的必經點

例題：HDOJ Important Sisters

模型：給定有向圖G（可能有環）和圖中的一個點r，對於G中的任何一個點x，從r到x的所有路徑上必經的點集。

顯然可以暴力求解
Tarjan有一個更好的解決方法——支配樹

半必經點：

半必經點

·在搜尋樹T上點y的祖先中，經過時間戳比y大的節點可以到達y的深度最小的祖先x，成為y的半必經點。

·半必經點也是唯一的，因此可以記x=semi(y)

But！！半不經點不一定是必經點

ps：以下內容瞭解即可

Lengauer—Tarjan演算法

在訪問每個節點時，把該節點放入圖的一個生成森林中。
使用並查集維護生成森林，把dfn[semi[z]]作為z到其父節點的邊的權值

虛擬碼：

一般有向圖的必經邊

給定一張Flow Graph（G，r），若去掉圖中的一條邊e後，r不能到達途中的全部節點，則稱e是（G，r）的橋